Бесконечно малые, бесконечно большие и локально ограниченные функции

Функция 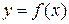называется бесконечно малой при 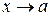, если (рис. 5, 6).

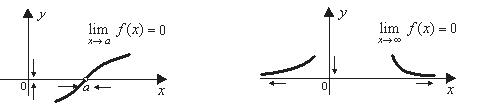
Рис. 5 Рис. 6

Пример: – бесконечно малая функция при .

Две бесконечно малые при функции f (x) и g (x) называются эквивалентными бесконечно малыми, если .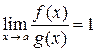

Основные соотношения эквивалентностей:

при , (1)

при , (2)

при , (3)

при , (4)

при , (5)

при , (6)

при . (7)

Функция 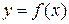называется бесконечно большой при 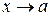, если для любого числа , сколь бы большим оно ни было, можно указать такую окрестность U (a) точки х = а (не включающую саму точку а), что при всех х, принадлежащих этой окрестности, выполняется неравенство .

Предел бесконечно большой функции при 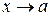обозначается симво-лом ¥: и называется бесконечным пределом функции при x ® a.

Определение бесконечно большой функции при x ® a можно записать символически следующим образом:

.

Геометрически существование бесконечного предела
означает, что значения функции 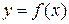становятся сколь угодно большими по модулю, если значения аргумента достаточно близки к точке х = а (рис. 7, 8).

Рис. 7 Рис. 8

Пример. – бесконечно большая функция при x ® 1.

Бесконечный предел последовательности означает, что члены последовательности становятся сколь угодно большими по модулю при достаточно больших номерах n:

.

Функция 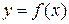называется локально ограниченной в точке х = а, если существует такая окрестность точки U (a), в которой значения функции удовлетворяют неравенству , где m и M – некоторые числа.

Любая функция, имеющая конечный предел при x ® a, в том числе
и бесконечно малая функция, является локально ограниченной в точке х = а.

Если 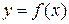– бесконечно большая при x ® a, то она не является локально ограниченной в точке х = а.

Пример. – локально ограниченная функция во всех точках, кроме точек х = 1 и х = –1.

Вычисление пределов

При вычислении пределов используют теоремы о конечных пределах и теоремы обесконечно малых и бесконечно больших функциях.

Основные теоремы о конечных пределах

1. Если f (x) = const (const – константа) при ,
то .

2. , где C = const.

3. , если f (x) – функция, непрерывная в точке х = а
(см. п. 6).

4. Если и , где – числа,
то , и при условии, что A₂ ¹ 0.

Теоремы обесконечно малых и бесконечно больших функциях (для краткости обозначим: бм – бесконечно малая функция, бб – бесконечно большая функция, огр – локально ограниченная функция).

5. бм ± бм = бм.

6. бм × бм = бм.

7. бм × огр = бм.

8. , если огр не является бм.

9. бб + бб = бб, если обе бб одного знака.

10. бб × бб = бб.

11. бб × огр = бб, если огр не является бм.

12. .

Примеры.

1) (здесь использована теорема 1);

2) (здесь использованы теоремы 2, 3 и непрерывность функции у = 2 х – 1);

3) (здесь использована теорема 8);

4) (здесь использованы теоремы 2, 4 и 12).