МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
"МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"
Кафедра высшей математики
и программного обеспечения ЭВМ
ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ. КОМПЛЕКСНЫЕ ЧИСЛА. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Часть 2
Методические рекомендации к выполнению контрольных работ
для студентов 1 курса вечерне-заочного факультета
по дисциплине "Математика"
Мурманск
УДК 517 (076.5)
ББК 22.161Я73
М 54
Составители: В.С. Кацуба, канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ;
Л.Г. Мостовская, доцент кафедры высшей математики
и программного обеспечения ЭВМ МГТУ
Методические рекомендации рассмотрены и одобрены кафедрой
13 декабря 2006 г., протокол № 3
Рецензент – Ю.П. Драница, канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ
Оригинал-макет подготовлен в авторской редакции
Электронная верстка О.Р. Аптышевой
Мурманский государственный технический университет, 2007
Оглавление
Введение.. 4
Методические указания по темАМ "Элементы теории функций. Комплексные числа" и "Дифференциальное исчисление функции одной переменной". 5
Справочный материал по теме "Элементы теории функций. Комплексные числа". 6
1. Функции и их свойства. 6
2. Предел функции. Предел последовательности. 9
3. Бесконечно малые, бесконечно большие и локально ограниченные функции 11
4. Вычисление пределов. 13
5. Раскрытие неопределенностей. 14
6. Непрерывность функции, точки разрыва. 16
7. Комплексные числа. 18
8. Действия над комплексными числами. 20
Примерный вариант и образец выполнения
контрольной работы 3. 21
Справочный материал по теме "Дифференциальное исчисление функциЙ одной переменной". 31
1. Дифференцирование функций. 31
2. Уравнения касательной и нормали к плоской кривой. 33
3. Вычисление пределов при помощи правила Лопиталя. 33
4. Исследование функций и построение графиков. 34
Примерный вариант и образец выполнения
контрольной работы 4. 38
Варианты контрольнЫХ работ.. 46
Варианты контрольной работы 3. 47
Варианты контрольной работы 4. 51
Рекомендуемая литература.. 54
Введение
В настоящем пособии содержатся методические рекомендации
к изучению теоретического материала и выполнению контрольных работ по темам "Элементы теории функций. Комплексные числа" и "Дифференциальное исчисление функций одной переменной", а также варианты
контрольных работ 3 и 4 по этим темам для студентов ВЗФ.
В результате изучения этих тем студенты 1-го курса должны:
• владеть понятиями функции, сложной и обратной функций, знать свойства основных элементарных функций, уметь определять их основные характеристики по графикам функций;
• знать определения предела функции и предела последовательности;
• уметь вычислять пределы, раскрывать неопределенности и анализи-ровать полученный результат с точки зрения определения предела;
• уметь исследовать функции на непрерывность, определять точки разрыва функции и устанавливать тип разрыва;
• знать, что такое мнимая единица и комплексное число, уметь производить операции над комплексными числами в алгебраической и тригонометрической формах;
• уметь решать простейшие алгебраические уравнения на множестве комплексных чисел;
• владеть основными понятиями дифференциального исчисления (производная и ее геометрический смысл, дифференциал), уметь находить производные функций, заданных явно, неявно или параметрически;
• иметь навыки решения основных задач с использованием производных: геометрические задачи на касательную и нормаль, вычисление пределов
с использованием правила Лопиталя и пр.;
• знать приемы исследования функций с помощью производной.
Данные методические рекомендации включают также список рекомендуемой литературы, справочный материал, необходимый для выполнения контрольных работ 3 и 4 для студентов 1-го курса и решение примерных вариантов этих работ, в которых имеются ссылки на используемый справочный материал.
Методические указания по темАМ
"Элементы теории функций. Комплексные числа"
и "Дифференциальное исчисление функции
одной переменной"
В таблице 1 приведены наименования тем в соответствии с содержанием контрольных работ и ссылки на литературу по этим темам. Перед выполнением каждой из контрольных работ рекомендуется изучить соответствующий теоретический материал и решить указанные в таблице задачи.
Таблица 1
| № к. раб. | № задачи | Содержание (темы) | Литература |
| Основные элементарные функции, их графики и основные характеристики. Сложные функции. Обратные функции | [1], гл. V, § 14; [2], гл. 4, § 1, 11, 12.1; [3], гл. VI, № 610 – 637; [4], гл. 4, № 15 – 38, 43 – 60, 62–71, 73–108, 151, 153 | ||
| Предел числовой последовательности и функции непрерывного аргумента. Вычисление пределов, раскрытие основных видов неопределенностей. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции | [1], гл. V, § 15–18; [2], гл. 4, § 2–6; [3], гл. VI, № 638–690, 692, 693, 700, 707, 714–719; [4], гл. 2, № 21–24, 26–28, 63–68, гл. 4, № 228–246, 285, 289, 346–351, 355, 358–359 | ||
| Определение непрерывности функции в точке и на промежутке. Точки разрыва функции и их классификация. Исследование функции на непрерывность | [1], гл. V, § 19; [2], гл. 4, § 7–9; [3], гл. VI, № 723–735 | ||
| Комплексные числа. Действия над комплексными числами в алгебраической и тригонометрической формах. Решение простейших алгебраических уравнений на множестве комплексных чисел | [1], гл. VI, § 27–28; [2], гл. 14, § 6.1; [4], гл. 9, № 1–52 |
Окончание табл. 1
| № к. раб. | № задачи | Содержание (темы) | Литература |
| Определение производной. Правила дифференцирования. Производные основных элементарных функций. Производные сложных функций. Дифференцирование функций, заданных неявно и параметрически. Производные высших порядков | [1], гл.V, § 20, 21, 23.1; [2], гл. 5, § 1, 4, 5, 7–9, 10.1, 11; [3], гл. VII, № 771–811, 900–907, 909–912, 950, 951, 964, 965, 969; [4], гл. 5, № 14–44, 162–167, 206–211 | ||
| Уравнения касательной и нормали к плоской кривой | [1], гл. V, § 20.2; [2], гл. 5, § 1.2; [3], гл. VII, № 917–921, 923–930; [4], гл. 5, № 139–144 | ||
| Вычисление пределов при помощи правила Лопиталя | [1], гл. V, § 25.2; [2], гл. 6, § 1, 2; [3], гл. VII, № 1024–1028, 1030–1040; [4], гл. 5, № 225–240, 258–264 | ||
| Монотонность и экстремумы функций. Выпуклость графика функции, точки перегиба. Вертикальные и наклонные асимптоты. Полное исследование функции и построение ее графика | [1], гл. V, § 25.3–25.8; [2], гл. 6, § 4; [3], гл. VII, № 1055–1058, 1061–1064, 1083–1084, 1091–1094, 1102–1109; [4], гл. 5, № 282, 293, 296, 297–300, 315–324, 334, 339, 342, 344–347 |
Примечание. Ссылки на литературу в таблице даны в соответствии
с номерами в списке рекомендуемой литературы.
Справочный материал по теме
"Элементы теории функций. Комплексные числа"
Функции и их свойства
Переменной называют величину x Î X, принимающую значения из некоторого множества значений Х.
Если каждому значению переменной х из множества Х поставлено
в соответствие по определенному правилу f единственное значение пере-менной у из множества Y, то говорят, что задана функция 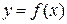 , определенная на множестве Х с множеством значений Y. При этом используют следующие названия:
, определенная на множестве Х с множеством значений Y. При этом используют следующие названия:
х – аргумент (независимая переменная);
у – значение функции (зависимая переменная);
Х – область определения функции (ООФ);
Y – множество значений функции (ОЗФ).
Функция 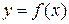 , область определения Х которой симметрична
, область определения Х которой симметрична
относительно начала координат, называется четной, если 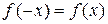 ,
,
и называется нечетной, если  , "
, "  .
.
Примеры. y = cos x – четная функция, y = x 3 – нечетная функция, 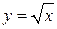 – функция общего вида (ни четная, ни нечетная).
– функция общего вида (ни четная, ни нечетная).
Функция 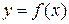 называется периодической, если существует положительное число Т, такое, что
называется периодической, если существует положительное число Т, такое, что 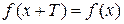 , " x Î X.
, " x Î X.
Примеры. y = tg x – периодическая функция, наименьший период T = π, y = ln x – непериодическая функция.
Значение функции  – переменная величина, поэтому можно рассматривать новую функцию с аргументом у: z = g (y), где
– переменная величина, поэтому можно рассматривать новую функцию с аргументом у: z = g (y), где  ,
,
т. е. функцию z = g (f (x)). Такая функция называется сложной функцией
от х, или суперпозицией функций f и g.
Пример. z = tg (х 2 + 3 x – 1)– суперпозиция функций z = tg у
и у = х 2 + 3 x – 1.
Если  ставится в соответствие единственное значение
ставится в соответствие единственное значение  , такое, что
, такое, что 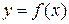 , то говорят, что задана функция
, то говорят, что задана функция  , которую называют обратной по отношению к функции
, которую называют обратной по отношению к функции 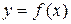 . Функции f и
. Функции f и 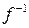 называются взаимно обратными функциями. Если у обратной функции
называются взаимно обратными функциями. Если у обратной функции  обозначить аргумент буквой х, а функцию – буквой у,
обозначить аргумент буквой х, а функцию – буквой у,
то графики взаимно обратных функций  и
и  будут симметричны относительно прямой у = х.
будут симметричны относительно прямой у = х.
Пример. y = lg x и y = 10 x – взаимно обратные функции.
Все функции, задаваемые аналитическим способом, можно разбить
на два класса: элементарные и неэлементарные. В классе элементарных функций выделяют основные элементарные функции: степенная (у = xn), показательные (y = ax), тригонометрические (y = sin x, y = cos x, y = tg x, y = ctg x), а также обратные к ним (логарифмические, обратные тригонометрические и др.). Элементарными называют функции, полученные из основных элементарных функций при помощи конечного числа операций сложения, вычитания, умножения, деления, а также суперпозиции основных элемен-тарных функций. Все остальные функции относятся к неэлементарным.
Примеры. y = lg (cos x) – элементарная функция, так как является суперпозицией основных элементарных функций y = lg x и y = cos x;  – неэлементарная функция.
– неэлементарная функция.
Нулями функции 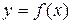 называют точки х, в которых выполнено равенство
называют точки х, в которых выполнено равенство  . Нули функции – это абсциссы точек пересечения графика функции с осью Oх.
. Нули функции – это абсциссы точек пересечения графика функции с осью Oх.
Пример. У функции y = lg (x) единственный нуль – точка х = 1.
Функция 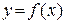 называется монотонно возрастающей на интервале х Î (а; b), если для любых двух точек х 1 и х 2 этого интервала из неравенства х2 > х 1 следует неравенство
называется монотонно возрастающей на интервале х Î (а; b), если для любых двух точек х 1 и х 2 этого интервала из неравенства х2 > х 1 следует неравенство 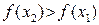 , то есть если любому большему значению аргумента из этого интервала соответствует большее значение функции.
, то есть если любому большему значению аргумента из этого интервала соответствует большее значение функции.
Функция 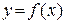 называется монотонно убывающей на интервале х Î (а; b), если для любых двух точек х 1 и х 2 этого интервала из неравенства х 2 > х 1 следует неравенство
называется монотонно убывающей на интервале х Î (а; b), если для любых двух точек х 1 и х 2 этого интервала из неравенства х 2 > х 1 следует неравенство 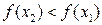 .
.
Промежутки возрастания и убывания функции называются промежутками монотонности функции.
Если функция 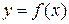 монотонна на интервале х Î(а; b), то она имеет обратную функцию
монотонна на интервале х Î(а; b), то она имеет обратную функцию  .
.
Пример. Функция y = tg x монотонна на интервале  , ее ОЗФ:
, ее ОЗФ:  . Она имеет обратную функцию y = arctg x, определенную на интервале
. Она имеет обратную функцию y = arctg x, определенную на интервале 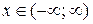 , с ОЗФ:
, с ОЗФ: 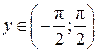 .
.
Точка х 0 называется точкой максимума функции 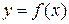 , если суще-ствует такая двухсторонняя окрестность точки х 0, что для всякой точки х ¹ х 0 этой окрестности выполняется неравенство
, если суще-ствует такая двухсторонняя окрестность точки х 0, что для всякой точки х ¹ х 0 этой окрестности выполняется неравенство 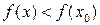 . При этом число
. При этом число 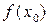 называется максимумом функции
называется максимумом функции 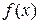 и обозначается y max.
и обозначается y max.
Аналогично, если для всякой точки х ¹ х 0 из некоторой окрестности точки  выполняется неравенство
выполняется неравенство 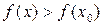 , то
, то  называется точкой минимума, а число
называется точкой минимума, а число 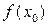 – минимумом функции
– минимумом функции 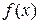 и обозначается y min.
и обозначается y min.
Точки максимумов и минимумов называются точками экстремумов функции, а числа y max и y min называются экстремумами функции.
Пример. Функция y = cos x имеет точки максимумов x = 2p k, k = 0, ±1, ±2, …, 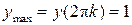 , и точки минимумов x = p + 2p k, k = 0, ±1, ±2, …,
, и точки минимумов x = p + 2p k, k = 0, ±1, ±2, …, 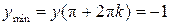 .
.
Предел функции. Предел последовательности
Пусть функция 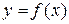 определена в некоторой окрестности точки х = а, где а – конечная или бесконечно удаленная точка на числовой
определена в некоторой окрестности точки х = а, где а – конечная или бесконечно удаленная точка на числовой
прямой Ох.
Число А называется конечным пределом функции 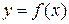 в точке х = а (или при
в точке х = а (или при 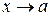 ), если для любого числа
), если для любого числа 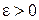 , сколь малым бы оно ни было, можно указать такую окрестность U (a) точки х = а (не включающую саму точку а), что при всех х, принадлежащих этой окрестности, выполняется неравенство
, сколь малым бы оно ни было, можно указать такую окрестность U (a) точки х = а (не включающую саму точку а), что при всех х, принадлежащих этой окрестности, выполняется неравенство 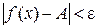 .
.
Предел функции обозначается так:  , или
, или 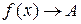 при
при 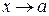 .
.
Определение конечного предела при 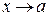 можно записать символически следующим образом:
можно записать символически следующим образом:
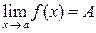
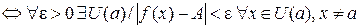 . (*)
. (*)
Геометрически существование конечного предела 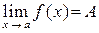 в случае, когда
в случае, когда 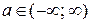 , означает, что значения функции
, означает, что значения функции 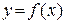 сколь угодно мало отличаются от числа А, если значения аргумента становятся достаточно близкими к точке
сколь угодно мало отличаются от числа А, если значения аргумента становятся достаточно близкими к точке 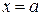 (рис. 1). При этом в самой точке а функцияможет быть не определена или определена, но может иметь значение, отличное от А.
(рис. 1). При этом в самой точке а функцияможет быть не определена или определена, но может иметь значение, отличное от А.
Поведение функции только слева или только справа от точки 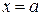 , т. е. в ее левой или правой окрестности, характеризуется ее односторонними пределами (рис. 2): левосторонний предел функции обозначается
, т. е. в ее левой или правой окрестности, характеризуется ее односторонними пределами (рис. 2): левосторонний предел функции обозначается  , где условие
, где условие 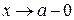 означет, что х остается левее точки а (
означет, что х остается левее точки а (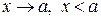 ); правосторонний предел функции обозначается
); правосторонний предел функции обозначается 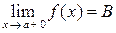 , где условие
, где условие  означет, что х остается правее точки а (x ® a, x > a).
означет, что х остается правее точки а (x ® a, x > a).

Рис. 1 Рис. 2
Существование предела 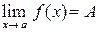 означает, что существуют оба односторонних предела и они совпадают между собой:
означает, что существуют оба односторонних предела и они совпадают между собой:
 .
.
Если существует конечный предел функции при  :
: 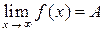 , то в его определении (*) U (a) – это окрестность бесконечно удаленной точки числовой прямой (рис. 3). При этом можно рассматривать односторонние пределы:
, то в его определении (*) U (a) – это окрестность бесконечно удаленной точки числовой прямой (рис. 3). При этом можно рассматривать односторонние пределы:  или
или 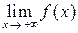 (рис. 4).
(рис. 4).
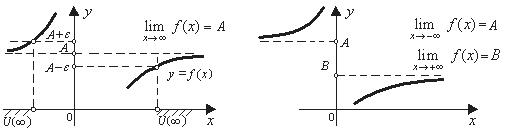
Рис. 3 Рис. 4
Числовую последовательность  обычно рассматривают как функцию натурального аргумента n:
обычно рассматривают как функцию натурального аргумента n:  .
.
Если существует предел последовательности 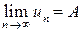 , то его определение можно записать символически:
, то его определение можно записать символически:
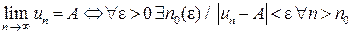 ,
,
т. е. члены последовательности  сколь угодно мало отличаются
сколь угодно мало отличаются
от числа А при достаточно больших номерах n (для n > n0).






