Так как 
и 
, то число 
является корнем многочленов 
и 
, т.е. они делятся без остатка на 
.
Тогда
, 
.
.
Подставляя в предел вместо x число –3, получаем снова неопределенность 
, а значит нужно опять разложить на множители числитель и знаменатель дроби. Это можно сделать путем нахождения корней квадратных трехчленов, стоящих в числителе и знаменателе.
.
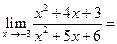
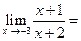
Ответ: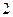 
.
Задача 10. Вычислить предел функции 
.
Решение. При вычислении предела функции, прежде всего, следует найти вид неопределенности. Видим, что предел нужно найти от отношения двух иррациональных выражений. Подставляя вместо x число –8, получим вид неопределенности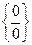 
. В этом случае для того, чтобы неопределенность исчезла (для раскрытия неопределенности), необходимо в числителе и знаменателе иррациональность перевести на противоположную сторону дроби (из числителя в знаменатель или наоборот) и после приведения подобных членов сократить числитель и знаменатель на общий множитель.
Используем формулы:
для числителя, 
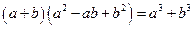для знаменателя.
= 
.
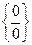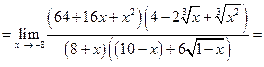
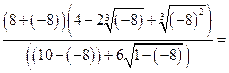
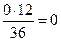Ответ:0.
Задача 11. Вычислить предел функции 
.
Решение. При вычислении предела функции, прежде всего, следует найти вид неопределенности. Подставляя вместо x число 0, получим отношение двух бесконечно малых функций и вид неопределенности 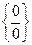. Воспользуемся для решения таблицей эквивалентных бесконечно малых функций.
.
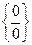
Ответ: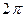 
.
Задача 12. Вычислить предел функции 
.
Решение. При вычислении предела функции, прежде всего, следует найти вид неопределенности. Подставляя вместо x число p, получим отношение двух бесконечно малых функций и вид неопределенности 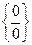. Поскольку таблица эквивалентных бесконечно малых функций получена при условии, что аргумент функций 
, то для удобства использования таблицы сделаем замену таким образом, чтобы новая переменная стремилась к нулю.
.
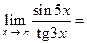
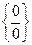
Ответ: 
.
Задача 13. Вычислить предел функции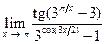 
.
Решение. При вычислении предела функции, прежде всего, следует найти вид неопределенности. Подставляя вместо x число p, получим отношение двух бесконечно малых функций и вид неопределенности 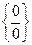. Поскольку таблица эквивалентных бесконечно малых функций получена при условии, что аргумент функций , то для удобства использования таблицы сделаем замену таким образом, чтобы новая переменная стремилась к нулю.
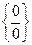
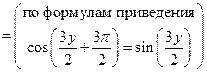
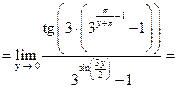
Ответ: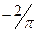 
.
Задача 14. Вычислить предел функции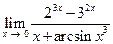 
.
Решение. При вычислении предела функции, прежде всего, следует найти вид неопределенности. Подставляя вместо x число 0, получим отношение двух бесконечно малых функций и вид неопределенности 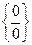. Поскольку замену на эквивалентные функции можно производить только в произведении и частном, необходимо преобразовать выражение к частному, например путем вынесения общего множителя или вынесением переменной x. Затем заменяем бесконечно малые функции на эквивалентные функции.
.
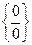
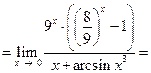
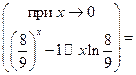
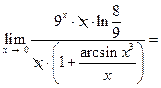
Ответ: 
.
Задача 15. Вычислить предел функции 
.
Решение. При вычислении предела функции, прежде всего, следует найти вид неопределенности. Подставляя вместо x число 0, получим отношение двух бесконечно малых функций и вид неопределенности 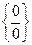. Поскольку таблица эквивалентных бесконечно малых функций получена при условии, что аргумент функций , то для удобства использования таблицы сделаем замену таким образом, чтобы новая переменная стремилась к нулю.
.
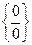
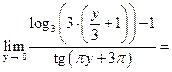
Ответ: 
.
Задача 16. Вычислить предел функции 
.
Решение. При вычислении предела функции, прежде всего, следует найти вид неопределенности. Подставляя вместо x число 0, получим вид неопределенности 
. Этот вид неопределенности требует особого подхода к его раскрытию.
Способ 1. С помощью некоторых преобразований привести предел ко второму замечательному пределу: 
, где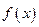 
— бесконечно малая функция при x → 0.
.
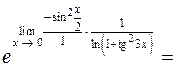
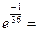
Способ 2. Поскольку мы имеем дело со степенно-показательной функцией, то можем преобразовать ее к показательной функции
и затем вычислить предел.
.
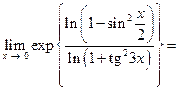
Ответ: .
Задача 17. Вычислить предел функции 
.
Решение. При вычислении предела функции, прежде всего, следует найти вид неопределенности. Подставляя вместо x число 0, получим отношение двух бесконечно малых функций и неопределенность 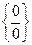, которая легко раскрывается путем замены бесконечно малых функций на эквивалентные функции.
.
Ответ: .
Задача 18. Вычислить предел функции 
.
Решение. При вычислении предела функции, прежде всего, следует найти вид неопределенности. Подставляя вместо x число p, получим вид неопределенности . Этот вид неопределенности требует особого подхода к его раскрытию.
С помощью некоторых преобразований привести предел ко второму замечательному пределу: , где 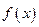— бесконечно малая функция при x → 0.
.
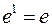Ответ: 
.
Задача 19. Вычислить предел функции 
.
Решение. При вычислении предела функции, прежде всего, следует найти вид неопределенности. Подставляя вместо x число 1, получим отношение двух бесконечно малых функций и неопределенность 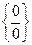, которая легко раскрывается путем замены бесконечно малых функций на эквивалентные функции.
.
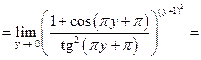
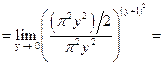
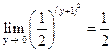Ответ: 
.
Задача 20. Вычислить предел функции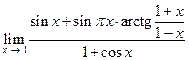 
.
Решение. При вычислении предела функции, прежде всего, следует найти вид неопределенности. Подставляя вместо x число 1, получим, поскольку
, 
,
.
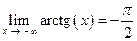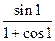Ответ: .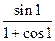
