1. Если основание стремится не к 1, а к числу a<1 а степень к бесконечности, то можно сразу сделать вывод, что предел 0. Если a>1 то наоборот, 
.
, 
2. Не всегда в степени экспоненты получается конечное число. Так, в примере
= 
= 
= 
= 
. Это произошло из-за того, что в степени в её знаменателе остался множитель 
.
Повторные и двойные пределы.
А является пределом функции 
в точке 
, если для всякого 
существует окрестность 
точки , так что если 
, то 
. Обозначается 
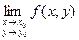- двойной предел.
, 
«повторные» пределы.
Пример. 
. Повторные 0
если приближаться к точке (0,0) по прямой 
= 
.
Практика 18
Главная часть бесконечно-малой.
Задача 1. Найти главную часть для 
в точке х = 1 вида 
.
Видно, что это действительно бесконечно-малая в точке 1, 
.
Метод: запишем в знаменателе и приравняем предел к единице, ведь эти величины должны быть эквивалентны. Затем ведём преобразования и упрощаем выражение под знаком предела, как при обычном вычислении предела. Когда оно упростится настолько, что все 
можно будет собрать в отдельный множитель, а все остальные, не стремящиеся к нулю, отдельно, тогда легко определится k и С.
. Так как мы ищем эквивалентную, то предел равен 1.
. Представим в виде 
.
Во-первых, множители (x-1) полностью сократятся лишь в случае, когда k=1, иначе предел получился бы 0 или . Теперь, если уже известно, что k=1, и все множители типа (x-1) сократились, вычислим С.
, 
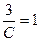, С = 3. Итак, 
.
На графике зелёным изображена главная часть , а коричневым .Мы фактически нашли среди степенных функций вида наилучшую, соответствующую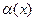 
.
Кстати, заметим, если порядок малости в данной точке равен 1, то есть k=1, то график пересекает ось Ох под каким-то углом, причём главная часть соответствует уравнению касательной. Если же касательная горизонтальна, то бесконечно малая имеет не 1 порядок, а более высокий.
Задача 2. Выделить главную часть бесконечно-малой: 
в точке 1.
Ответ.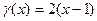 
.
Задача 3. Выделить главную часть бесконечно-малой: 
отв: 
Чертёж к этой задаче:
Практика 19
Непрерывность и точки разрыва. 45 минут.
Контрольная 45 минут.
9 Предел последовательности
10 Предел функции, с неопределённостью 0/0.
11 Предел функции, 1-й замеч. lim
12 Предел функции, 2-й замеч. lim
Приложение 1.
Пример одного варианта контрольных работ.
Темы 3-й контрольной:
9. Предел последовательности
10. Предел функции, с неопределённостью 0/0.
11. Предел функции, 1-й замеч. lim
12. Предел функции, 2-й замеч. lim
Вариант:
9) Вычислить предел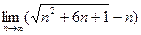 
10) Вычислить предел 
11) Вычислить предел 
12) Вычислить предел 
Темы 4-й контрольной:
13. Производные функции одной переменной.
14. Частные производные для f(x,y), градиент.
15. Уравнение касательной
15. Экстремумы функции на [a,b].
Вариант:
13) Найти производную (какая-нибудь функция f(x)).
14) Найти градиент функции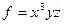 
в точке 
и производную по направлению 
.
15) Найти уравнение касательной для 
в точке 
и высоту касательной при x=0.
16) Найти экстремумы для 
.
