Томский государственный университет систем управления и радиоэлектроники
Приходовский М.А.
Математика
(1 семестр, часть 2)
Учебно-методическое пособие
для специальностей:
09.03.03 «прикладная информатика в экономике»
(группы 446-1 и 446-2)
Томск
ТУСУР
Электронное учебное пособие составлено и скорректировано с учётом реального проведения практических занятий на ФСУ в группах 446-1, 446-2 осенью 2016 года. В осеннем семестре, согласно рабочим программам, на специальности 09.03.03 изучаются следующие темы: линейная алгебра, аналитическая геометрия, введение в математический анализ, дифференциальное исчисление. Даны с подробным разбором задачи, которые решались на каждом практическим занятии. Пособие может представлять методический интерес для преподавателей, работающих на аналогичных специальностях, как материал для планирования занятий.
Содержание
Практика № 15 5
Практика № 16 13
Практика № 17 22
Практика № 18 31
Практика № 19
Практика № 20
Практика № 21
Практика № 22
Практика № 23
Практика № 24
Практика № 25
Приложение.
Номера практик по датам для групп 446-1, 446-2 согласно расписанию
| Практика № | 446-1 | 446-2 |
| 02.09.16 | 03.09.16 | |
| 06.09.16 | 03.09.16 | |
| 09.09.16 | 09.09.16 | |
| 16.09.16 | 17.09.16 | |
| 20.09.16 | 17.09.16 | |
| 23.09.16 | 23.09.16 | |
| 30.09.16 | 27.09.16 | |
| 04.10.16 | 27.09.16 | |
| 07.10.16 | 07.10.16 | |
| 14.10.16 | 11.10.16 | |
| 18.10.16 | 11.10.16 | |
| 21.10.16 | 21.10.16 | |
| 28.10.16 | 25.10.16 | |
| 01.11.16 | 25.10.16 | |
| 11.11.16 | 07.11.16 | |
| 15.11.16 | 07.11.16 | |
| 18.11.16 | 18.11.16 | |
| 25.11.16 | 21.11.16 | |
| 29.11.16 | 21.11.16 | |
| 02.12.16 | 02.12.16 | |
| 09.12.16 | 05.12.16 | |
| 13.12.16 | 05.12.16 | |
| 16.12.16 | 16.12.16 | |
| 23.12.16 | 19.12.16 | |
| 27.12.16 | 19.12.16 | |
| 30.12.16 | 30.12.16 |
Практика 15
«Введение в математический анализ. Множества и функции»
Задача 1. Доказать нечётность функции  .
.
Решение. Заменим  на
на  , при этом
, при этом  наоборот, заменится на
наоборот, заменится на  .
.
 =
=  =
= 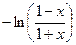 .
.
Таким образом,  , то есть функция нечётная.
, то есть функция нечётная.
Задача 2. Даны 2 функции:  ,
,  . Найти все их возможные композиции.
. Найти все их возможные композиции.
Решение.  так как
так как  то повторное вычисление синуса ещё чуть уменьшает значение этой величины, поэтому график суть ниже обычного графика синуса.
то повторное вычисление синуса ещё чуть уменьшает значение этой величины, поэтому график суть ниже обычного графика синуса.
Графики для сравнения:

 , здесь скорость возрастания с ростом
, здесь скорость возрастания с ростом  всё более увеличивается, то есть колебания синуса учащаются. График:
всё более увеличивается, то есть колебания синуса учащаются. График:

 ,график:
,график:

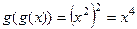 строение этой функции хорошо известно.
строение этой функции хорошо известно.
На чертеже зелёным показан график  , синим
, синим  .
.

Задача 3. Найти композицию  если
если 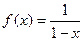 .
.
Решение. Двойная композиция это  ,
,
а тройная композиция  . Можно сначала привести подобные внутри самой внутренней дроби, для чего 1 представим как
. Можно сначала привести подобные внутри самой внутренней дроби, для чего 1 представим как  .
.
 =
=  =
=  =
= 
И в этой дроби тоже приведём подобные таким же способом.
 =
=  =
= 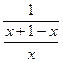 =
=  =
=  .
.
Ответ.  .
.
К задаче 4. Композиции функций из в и из в.
Функция  отображает
отображает 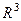 в
в  .
.
Функция из  в
в 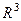 :
: 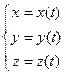 такая функция задаёт движение точки в пространстве.
такая функция задаёт движение точки в пространстве.
Можно рассматривать композицию: 

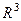

 .
.
 . Физический смысл: каждой точке пространства задана температура, и заданы параметрические уравнения движения точки в пространстве. По какому закону для этой точки будет изменяться окружающая температура.
. Физический смысл: каждой точке пространства задана температура, и заданы параметрические уравнения движения точки в пространстве. По какому закону для этой точки будет изменяться окружающая температура.
Задача 4. Точка движется по окружности единичного радиуса вокруг начала координат в плоскости. Температура распределена по закону:
 . Найти для этой точки функцию, как меняется температура в зависимости от времени.
. Найти для этой точки функцию, как меняется температура в зависимости от времени.
Решение. Движение точки можно задать так:  ,
,  .
.
Подставим эти выражения в  , чтобы получить композицию функций.
, чтобы получить композицию функций.  =
=  .
.
Ответ. Температура в зависимости от времени для этой точки изменяется так:  .
.
Задача 5. Найти область определения функции:  .
.
Решение. Выражение под каждым из корней должно быть  , а для второго даже строго больше 0, так как он в знаменателе.
, а для второго даже строго больше 0, так как он в знаменателе.
Получается система из 2 неравенств:  и
и  .
.


 ,
, 

 .
.
Итого, пересечение этих множеств: 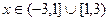 .
.
Ответ. 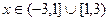 .
.
Задача 6. Найти область определения функции:
 .
.
Решение. Оба подкоренных выражения должны быть неотрицательны
 это область вне круга радиуса 1.
это область вне круга радиуса 1.
 это область внутри круга радиуса 3.
это область внутри круга радиуса 3.
В их пересечении лежит кольцо 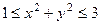 .
.
Чертёж:

Ответ. Кольцо 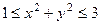 .
.
Задача 7. Найти область определения функции 3 переменных:
 .
.
Решение. Здесь  , т.е.
, т.е.  . Это неравенство задаёт шар радиуса 1. Штриховкой в плоскости, как в прошлой задаче, для функции трёх переменных изобразить уже невозможно.
. Это неравенство задаёт шар радиуса 1. Штриховкой в плоскости, как в прошлой задаче, для функции трёх переменных изобразить уже невозможно.
Ответ. Шар радиуса 1:  .
.
О комплексных числах. В следующем семестре мы будем подробно изучать такое расширение множества действительных чисел, как комплексные числа. Однако вкратце рассмотрим простейшие действия с ними уже сейчас, чтобы потом было легче понять.
Условно обозначим корень из  через
через  . Называется «мнимая единица». Такое число не существует на действительной прямой. Можно представить его в виде точки на вертикальной оси Оу в плоскости. Итак,
. Называется «мнимая единица». Такое число не существует на действительной прямой. Можно представить его в виде точки на вертикальной оси Оу в плоскости. Итак,  , то есть
, то есть 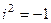 .
.
Каждой точке с координатами  в плоскости можно поставить в соответствие
в плоскости можно поставить в соответствие  , оно называется комплексным числом. Умножение таких чисел производится с помощью обычного раскрытия скобок с учётом того, что
, оно называется комплексным числом. Умножение таких чисел производится с помощью обычного раскрытия скобок с учётом того, что 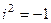 .
.
Задача 8. Умножить комплексные числа 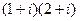 .
.
Решение. 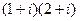 =
=  =
=  =
=
Ответ..
Задача 9. Найти корни многочлена  , где
, где  .
.
Решение. 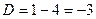 . Корни
. Корни  =
=  =
=  =
=  . Ответ.
. Ответ.  .
.
Перерыв в середине пары
Тема «Предел последовательности»
Задача 1. Найти предел  .
.
Решение. Здесь неопределённость типа 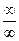 . Вынесем за скобки
. Вынесем за скобки  и в числителе, и в знаменателе, с целью сократить на этот множитель.
и в числителе, и в знаменателе, с целью сократить на этот множитель.
 =
=  =
= 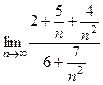
Каждая из мелких дробей в числителе и знаменателе стремится к 0,
поэтому получается сумма пределов в каждом случае, и тогда
 =
=  . Ответ.
. Ответ.  .
.
Задача 2. Найти предел  .
.
Решение. Здесь неопределённость типа 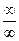 . Вынесем за скобки и сократим самую старшую степень элемента
. Вынесем за скобки и сократим самую старшую степень элемента  , в прошлой задаче это была 2-я степень, а здесь 3-я.
, в прошлой задаче это была 2-я степень, а здесь 3-я.
 =
=  =
=  =
=  . Ответ.
. Ответ.  .
.
Задача 3. Найти предел 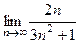 .
.
Решение. 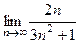 =
=  =
=  .
.
Замечание. Если наоборот, в знаменателе была бы степень больше, чем в числителе, то ответ не 0 а  .
.
Ответ. 0.
Задача 4. Найти предел  .
.
Решение. Здесь неопределённость типа  .
.
Чтобы свести к дроби, и сокращать как в прошлых примерах, надо сначала домножить на «сопряжённое» выражение, то есть такое где вместо разности сумма, это позволит использовать формулу сокращённого умножения 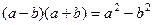 .
.
 =
=  =
=
 =
=  .
.
Теперь можно сократить на первую степень  :
:
 =
=  =
= 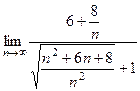 =
=  =
=  =
=  = 3. Ответ. 3.
= 3. Ответ. 3.
Задача 5. Найти предел  .
.
Решение. Сначала домножим на сопряжённое выражение, так как здесь есть разность, содержащая  .
.
 =
=
 =
=  .
.
Нужно сокращать на  . При этом в знаменателе два множителя, можно каждый из них разделить на
. При этом в знаменателе два множителя, можно каждый из них разделить на  , тем самым весь знаменатель разделится на
, тем самым весь знаменатель разделится на  .
.
 =
=  =
=
 =
= 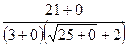 =
=  =
=
=  . Ответ. 1.
. Ответ. 1.
Задача 6. Найти предел  .
.
Решение. Здесь разности нет, так что можем сразу сократить на  .
.
В числителе при этом можно представить  в виде
в виде  .
.
 =
=  =
=  =
=
 = 2. Ответ. 2.
= 2. Ответ. 2.
Практика 16
Тема: Пределы функций.
Задача 1. Найти предел  .
.
Решение. Так как переменная неграниченно возрастает, то тоже влияют её старшие степени и коэффициенты перед ними.
Сократим дробь:  =
=  =
=  =
=  =
=  .
.
Ответ.  .
.
Задача 2. Найти предел  .
.
Решение. Аналогично тому, как в прошлом примере, сократим на старшую степень, здесь это  .
.
 =
=  =
=  =
=  =
=  .
.
Ответ.  .
.
Задача 3. Найти предел 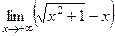 .
.
Решение. В этом примере надо домножить и поделить на «сопряжённое» то есть на сумму, чтобы использовать формулу 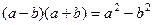 .
.
 =
= 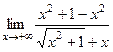 =
= 
здесь числитель равен 1, знаменатель неограниченно возрастает, поэтому получается выражение типа  , предел равен 0.
, предел равен 0.
Ответ. 0.
Замечание. Как мы видим, методы решения примеров для последовательности (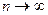 ) и для функции при
) и для функции при  во многом очень похожи. В одном случае дискретно увеличивается к бесконечности, а в другом непрерывно, но всё равно и там, и здесь неограниченное возрастание..
во многом очень похожи. В одном случае дискретно увеличивается к бесконечности, а в другом непрерывно, но всё равно и там, и здесь неограниченное возрастание..
Задача 4. Найти предел  .
.
Решение. В этом примере тоже надо домножить и поделить на «сопряжённое».
 =
=  =
=  теперь сократим на
теперь сократим на  :
: 
В знаменателе можно представить  в виде
в виде  , чтобы упростить выражение в знаменателе:
, чтобы упростить выражение в знаменателе:
 =
=  =
= 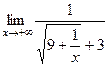 =
=  =
=  . Ответ.
. Ответ.  .
.
Примеры, в которых.
Задача 5. Найти предел  .
.
Решение. В этом случае  стремится к числу, а не бесконечности. Получается неопределённость совсем другого типа: если в прошлых примерах было
стремится к числу, а не бесконечности. Получается неопределённость совсем другого типа: если в прошлых примерах было  или
или 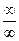 , то здесь
, то здесь  . Если просто подставить 1 в это выражение, получилось бы
. Если просто подставить 1 в это выражение, получилось бы  . Поэтому и нельзя просто подставить и вычислить значение, а нужно раскрывать неопределённость. Выделим множитель
. Поэтому и нельзя просто подставить и вычислить значение, а нужно раскрывать неопределённость. Выделим множитель  и в числителе, и в знаменателе, чтобы его сократить.
и в числителе, и в знаменателе, чтобы его сократить.
 =
=  =
=  = 2.
= 2.
Когда сократили, тогда уже можно просто подставить 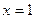 .
.
Ответ. 2.
Задача 6. Найти предел  .
.
Решение. Найдём корни многочленов в числителе и знаменателе, и разложим на множители.  =
=
=  =
=  . Сократили тот множитель, который отвечает за стремление к нулю, в числителе и знаменателе.
. Сократили тот множитель, который отвечает за стремление к нулю, в числителе и знаменателе.
Ответ.  .
.
Задача 7. Найти предел  .
.
Решение. Разложим на множители, как и в прошлой задаче.
 =
= 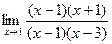 =
= 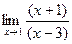 =
=  .
.
Нашли корни числителя и знаменателя, разложили на множители. Сократили тот множитель, который отвечает за стремление к нулю, в числителе и знаменателе.
Ответ.  .
.
(!) Обратите внимание, что в случае, когда в числителе таких множителей (стремящихся к 0) больше, чем в знаменателе, то происходит неполное сокращение, и в числителе остаётся одна из скобок, стремящихся к 0, то есть предел получается 0. Это будет видно на следующем примере.
Задача 8. Найти предел  .
.
Решение.  =
=  =
=  =
=  . В числителе остался один не сокращённый множитель
. В числителе остался один не сокращённый множитель  , остальные стремятся к константам, но уже не важно к каким, всё равно получится 0 из-за нуля в числителе.
, остальные стремятся к константам, но уже не важно к каким, всё равно получится 0 из-за нуля в числителе.
Ответ. 0.
Замечание. Наоборот, если бы такой множитель остался в знаменателе, то предел был бы равен  .
. 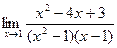 =
=  .
.
Задача 9. Найти предел  .
.
Решение. Во-первых, если просто подставить  , видно неопределённость
, видно неопределённость  . Это означает, что
. Это означает, что  является корнем, т.е. по крайней мере, хотя бы один множитель вида
является корнем, т.е. по крайней мере, хотя бы один множитель вида  и в числителе, и в знаменателе найдётся. Это облегчает поиск корней, можно обойтись даже без дискриминанта, а просто найти второй дополняющий. Когда мы сократим все
и в числителе, и в знаменателе найдётся. Это облегчает поиск корней, можно обойтись даже без дискриминанта, а просто найти второй дополняющий. Когда мы сократим все  , можно будет просто подставить
, можно будет просто подставить  в оставшееся выражение.
в оставшееся выражение.
 =
=  =
=  =
=  =
= 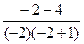 =
=  .
.
Ответ.  .
.
Задача 10. Найти предел  .
.
Решение. Способ 1. Тот факт, что при подстановке 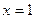 и в числителе, и в знаменателе даёт значение 0, говорит о том, что множитель
и в числителе, и в знаменателе даёт значение 0, говорит о том, что множитель  присутствует хотя бы один раз. Поэтому найти корни можно даже без дискриминанта.
присутствует хотя бы один раз. Поэтому найти корни можно даже без дискриминанта.
 =
=  =
= 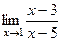 =
=  =
=  =
= 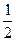 .
.
Способ 2. (Лопиталя).
 =
=  =
=  =
=  =
=  =
= 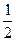 .
.
Ответ. 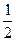 .
.
Задача 11. Найти предел  .
.
Решение. Воспользуемся формулой разности кубов:
 .
.
 =
=  =
=  = 27.
= 27.
Впрочем, можно сделать и методом Лопиталя:
 =
=  =
=  = 27.
= 27.
Ответ. 27.
Задача 12. Найти предел  .
.
Решение.  =
=  =
=  =
=  =
=  = 2.
= 2.
Замечание. Этот пример, как и многие из рассматриваемых, можно тоже для проверки решить вторым способом (Лопиталя).
Ответ. 2.
Задача 13. Найти предел  .
.
Решение. Здесь 3 степень в каждой части дроби, но зато мы точно знаем, что присутствует множитель  ведь неопределённость
ведь неопределённость  .
.
Это облегчает поиск корней многочленов 3-й степени: мы можем сначала поделить на  и останутся многочлены 2-й степени, корни которых уже можно найти через дискриминант.
и останутся многочлены 2-й степени, корни которых уже можно найти через дискриминант.


Итак,  =
= 
Однако находя корни через дискриминант, обнаруживаем, что ещё раз выделяется множитель  .
.
В числителе  , корни
, корни  , т.е.
, т.е.  и 1.
и 1.
В знаменателе  , корни
, корни  , т.е.
, т.е.  и 9.
и 9.
Получается 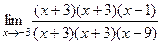 . Значит, просто эту скобку надо сократить 2 раза, но всё равно она ведь полностью сокращается.
. Значит, просто эту скобку надо сократить 2 раза, но всё равно она ведь полностью сокращается.
Получим  =
= 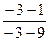 =
=  =
=  .
.
Замечание. 2-й способ. По методу Лопиталя здесь тоже пришлось бы дифференцировать 2 раза, из-за наличия корня кратности 2.
 =
=  .
.
Здесь опять получается неопределённость  , поэтому дальше:
, поэтому дальше:
 =
= 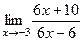 =
=  =
=  =
=  .
.
Ответ.  .
.
Задача 14. Найти предел  .
.
Решение. Сразу вынесем за скобку общий множитель и в числителе, и в знаменателе, там все остальные коэффициенты ему кратны. Затем разложим на множители.
 =
=  =
=  =
=
 =
=  =
=  .
.
Ответ.  .
.
Замечание. Если с самого начала не выносить старший коэффициент, то тогда надо не забыть домножить его потом, после разложения на множители. Ведь если просто записать разложение  то это равно
то это равно 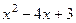 , а вовсе не
, а вовсе не  .
.
Задача 15. Найти предел  .
.
Решение. В отличие от прошлой задачи, здесь 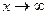 и поэтому другой тип неопределённости, и применяется совершенно другой метод решения, несмотря на то, что функция та же самая.
и поэтому другой тип неопределённости, и применяется совершенно другой метод решения, несмотря на то, что функция та же самая.
 =
=  =
= 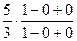 =
=  .
.
Ответ.  .
.
Замечание. Оба этих предела (в задачах 14 и 15) можно было найти по правилу Лопиталя. Если решать таким методом, то можно вообще не задумываться о том, надо ли выносить старший коэффициент.
 =
=  =
= 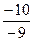 =
=  .
.
 =
=  =
=  =
=  .
.
Задача 16. Найти предел  .
.
Решение. Домножим и разделим на сопряжённое к каждой разности.
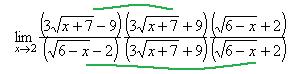
При этом соединим дугой те, которые в итоге сворачиваются в разность квадратов. Прочие множители, которые ни с чем не объединяются, вынесем в отдельную дробь, и даже в отдельный предел. Получается произведение пределов:

В одном из них нет неопределённости, а во втором преобразуем так, чтобы сократить скобку  .
.
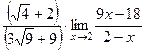 =
=  =
=  =
=  =
=  .
.
Ответ.  .
.
Задача 17-А. Найти предел  .
.
Задача 17-Б. Найти предел  .
.
Решение. Сейчас на этом примере мы увидим, как может отличаться решение и ответ в зависимости от 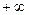 или
или 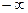 . И в том, и в другой случае мы стараемся сократить дробь на множитель
. И в том, и в другой случае мы стараемся сократить дробь на множитель  .
.
Если  положительно, то
положительно, то  можно представить в виде
можно представить в виде  .
.
 =
=  =
=  =
=  =
=  .
.
А вот если  отрицательно, то надо учесть, что
отрицательно, то надо учесть, что  это
это  , оно положительно, то есть при
, оно положительно, то есть при  верно
верно  . Поэтому
. Поэтому
 =
=  =
=  =
=  .
.
Ответы. 4 и  .
.
Практика 17 (18 ноября у обеих групп)
Задача 1. Найти предел 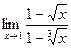 .
.
Решение. В этом случае можно с помощью замены преобразовать так, что будут только целые степени, а для получившихся многочленов уже можно искать корни и проводить разложение на множители.
НОК(2,3) = 6. Если обозначим  , то:
, то:
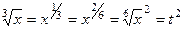 ,
,  .
.
При этом, если 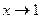 , то и
, то и  тоже стремится к 1.
тоже стремится к 1.
* Такое совпадение при замене переменной бывает далеко не всегда, а лишь в частных случаях, а обычно надо пересчитать, возможно новая переменная стремится к другому числу. Например, если  и
и  , то
, то  .
.
Итак, 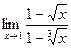 =
=  =
=  (для удобства сделали, чтобы многочлены начинались со старшей степени). Далее,
(для удобства сделали, чтобы многочлены начинались со старшей степени). Далее,
 =
= 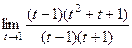 =
=  =
=  .
.
При этом даже нет необходимости делать обратную замену и возвращаться к старой переменной.
Ответ.  .
.






