Формулы полной вероятности и

БАЙЕСА

Часто мы начинаем анализ вероятностей имея предварительные, априорные значения вероятностей интересующих нас событий. Затем из источников информации, таких как выборка, отчет, опыт и т.д. мы получаем дополнительную информацию об интересующем нас событии. Имея эту новую информацию, мы можем уточнить, пересчитать значения априорных вероятностей. Новые значения вероятностей для тех же интересующих нас событий будут уже апостериорными ( послеопытными) вероятностями. Теорема Байеса дает нам правило для вычисления таких вероятностей.

Последовательность процесса переоценки вероятностей можно схематично изобразить так:

 

Априорные Новая информация из Байесовский Апостериорные

вероятности каких-либо источников анализ вероятности

 

Пусть событие А может осуществиться лишь вместе с одним из событий Н₁, Н₂, Н₃,..., Н_n, образующих полную группу. Пусть известны вероятности P(H₁), P(H₂),…P(H_i),…P(H_n). Так как события H_i образуют полную группу, то . Так же известны и условные вероятности события А: P(A/H₁), P(A/H₂), …P(A/H_i)…, P(A/H_n), i=1, 2, …, n. Так как заранее неизвестно с каким из событий H_i произойдет событие А, то события H_i называют гипотезами.

Необходимо определить вероятность события А и переоценить вероятности событий Hi с учетом полной информации о событии А.

Вероятность события А определяется как:

(3.1)

Эта вероятность называется полной вероятностью.

Если событие А может наступить только вместе с одним из событий Н1, Н2, Н3,..., Нn, образующих полную группу несовместных событий и называемых гипотезами, то вероятность события А равна сумме произведений вероятностей каждого из событий Н1, Н2,..., Нn на соответствующую условную вероятность события А.

Условные вероятности гипотез вычисляются по формуле:

 

или (3.2)

 

 

Это - формулы Байеса, (по имени английского математика Т.Байеса, опубликовавшего их в 1764 году) выражение в знаменателе - формула полной вероятности.

Пример 3.1. Предприятие, производящее компьютеры, получает одинаковые ЧИПы от двух поставщиков. Первый поставляет 65% ЧИПов, второй 35%. Известно, что качество поставляемых ЧИПов разное. Основываясь на предыдущих данных о рейтингах качества, составлена следующая таблица:

 

Поставщик	% качественной продукции	% брака
Поставщик 1
Поставщик 2

 

Предприятие осуществляет гарантийный ремонт компьютеров. Имея данные о числе компьютеров, поступающих на гарантийный ремонт в связи с неисправностью ЧИПов, переоцените вероятности того, что возвращенный для ремонта компьютер, укомплектован ЧИПом от поставщика 1, поставщика 2.

Решение задач с использованием формул полной вероятности и Байеса удобнее оформлять в виде таблицы следующего вида:

 

Гипотезы	Априорные вероятности	Условные вероятности	Совместные вероятности	Апостериорные вероятности P(Hi /A)

 

Шаг 1. В первой колонке перечисляем события, которые задают априорную информацию в контексте решаемой проблемы.

Соб. Н₁ - ЧИП от первого поставщика;

Соб. Н₂ - ЧИП от второго поставщика.

Это - гипотезы и они образуют полную группу независимых и несовместных событий.

Во второй колонке записываем вероятности этих событий:

Р(Н₁) = 0,65, а Р(Н₂) = 0,35

В третьей колонке определим условные вероятности события А - «ЧИП бракованный» для каждой из гипотез.

Шаг 2. В колонке 4 находим вероятности для событий «ЧИП от первого поставщика и он бракованный» и «ЧИП от второго поставщика и он бракованный». Они определяются по правилу умножения вероятностей путем перемножения значений колонок 2 и 3. Поскольку сформулированные события являются результатом пересечения двух событий: А и Hi, то их называют совместными вероятностями, то есть

Шаг 3. Суммируем вероятности в колонке 4 для того, чтобы найти вероятность события А. В нашем примере 0,0130 - вероятность поставки некачественного ЧИПа от поставщика1, 0,0175 - вероятность поставки некачественного ЧИПа от поставщика 2. Поскольку, как мы уже сказали выше, ЧИПы поступают только от двух поставщиков, то сумма вероятностей 0,0130 и 0,0175 показывает, что 0,0305 есть вероятность бракованного ЧИПа в общей поставке, по формуле (3.1):

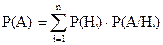= 0,0130 + 0,0175 = 0,0305

Шаг 4. В колонке 5 вычисляем апостериорные вероятности, используя формулу (3.2)

Заметим, что совместные вероятности находятся в строках колонки 4, а вероятность события А как сумма колонки 4.

Гипотезы	Априорные вероятности	Условные вероятности	Совместные вероятности	Апостериорные вероятности
ЧИП от 1-го поставщика ЧИП от 2-го поставщика	0,65   0,35	0,02   0,05	0,0130   0,0175	0,426   0,574
S		-	Р(А) = 0,305

Пример 3.2. Экономист полагает, что вероятность роста стоимости акций некоторой компании в следующем году равна 0,75, если экономика страны будет на подъёме; и эта же вероятность равна 0,30, если экономика страны не будет успешно развиваться. По его мнению, вероятность экономического подъёма в будущем году равна 0,80. Используя предположения экономиста, оцените вероятность того, что акции компании поднимутся в цене в следующем году?

Решение. Определим события:

А - “акции компании поднимутся в цене в будущем году”.

Событие А - “акции компании поднимутся в цене в будущем году” - может произойти только вместе с одной из гипотез:

Н₁ - экономика страны будет на подъёме и

Н₂ - экономика страны не будет успешно развиваться.

По условию известны вероятности гипотез:

P(H₁) = 0,8; P(H₂) = 0,2

и условные вероятности события А:

P(A/H₁) = 0,75; P(A/H₂) = 0,3.

Гипотезы образуют полную группу, сумма их вероятностей равна 1. Рассмотрим событие А - это (или Н₁А или Н₂А). События Н₁А и Н₂А - несовместные попарно, так как события Н₁ и Н₂ - несовместны.

События Н₁ и А, Н₂ и А - зависимые.

Вышеизложенное позволяет применить для определения искомой вероятности события А формулу полной вероятности:

P(A)=P(H₁) × P(A/H₁) + P(H₂) × P(A/H₂) = 0,8 × 0,75 + 0,2 × 0,3 = 0,66.

Оформим решение в рабочей таблице:

 

Гипотезы Hi	P(Hi)	P(A/Hi)	P(Hi)· P(A/Hi)
H1 - “подъем экономики”	0,80	0,75	0,60
H2- “спад экономики”	0,20	0,30	0,06
S	1,00	-	0,66

 

Ответ. Вероятность того, что акции компании поднимутся в цене в следующем году,

составляет 0,66.

 

Пример 3.3. Экономист полагает, что в течение периода активного экономического роста американский доллар будет расти в цене с вероятностью 0,7, в период умеренного экономического роста доллар подорожает с вероятностью 0,4 и при низких темпах экономического роста доллар подорожает с вероятностью 0,2. В течение любого периода времени вероятность активного экономического роста 0,3, умеренного экономического роста 0,5 и низкого роста - 0,2. Предположим, что доллар дорожает в течение текущего периода. Чему равна вероятность того, что анализируемый период совпал с периодом активного экономического роста?

Решение. Определим события:

А - “доллар дорожает”. Оно может произойти только вместе с одной из гипотез:

Н₁ - “активный экономический рост”;

Н₂ - “умеренный экономический рост”;

Н₃ - “низкий экономический рост”.

По условию известны доопытные (априорные) вероятности гипотез и условные вероятности события А:

Р(Н₁) = 0,3; Р(Н₂) = 0,5; Р(Н₃) = 0,2;

Р(А/Н₁) = 0,7; Р(А/Н₂) = 0,4 и Р(А/Н₃) = 0,2.

Гипотезы образуют полную группу, сумма их вероятностей равна 1. Событие А - это (или Н₁ × А или Н₂ × А или Н₃ × А). События Н₁ × А, Н₂ × А и Н₃ × А - несовместные попарно, так как события Н₁, Н₂ и Н₃ - несовместны.

События Н₁ и А, Н₂ и А, Н₃ и А - зависимые.

По условию требуется найти уточненную (послеопытную, апостериорную) вероятность первой гипотезы, т.е. необходимо найти вероятность активного экономического роста, при условии, что доллар дорожает (событие А уже произошло), то есть Р(Н₁/А) -?

Используя формулу Байеса (3.2) и подставляя заданные значения вероятностей, имеем:

Мы можем получить тот же результат при помощи таблицы:

Гипотезы Hi	Априорные вероятности P(Hi)	Условные вероятности P(A/Hi)	Совместные вероятности P(A Hi)	Апостериорные вероятности P(Hi/A)
H1	0,30	0,70	0,21	0,21 / 0,45 = 0,467
H2	0,50	0,40	0,20	0,20 / 0,45 = 0,444
H3	0,20	0,20	0,04	0,04 / 0,45 = 0,089
S	1,00	-	0,45

 

Ответ. Вероятность активного экономического роста, при условии, что доллар дорожает, составляет 0,467.

Для более наглядного восприятия решения нашей задачи мы можем также построить дерево решений:

 

		Совместные
Априорные	Условные	вероятности
вероятности	вероятности	(как произведение)
	P(A/H1) = 0,7	P(H1A) = 0,3× 0,7 = 0,21
Р(Н1) = 0,3
	P( /H1) = 0,3	P(H1 ) = 0,3× 0,3 = 0,09
Р(Н2) = 0,5	P(A/H2) = 0,4	P(H2A) = 0,5× 0,4 = 0,20
	P( /H2) = 0,6	P(H2 ) = 0,5× 0,6 = 0,30
	P(A/H3) = 0,2	P(H3A) = 0,2 × 0,2 = 0,04
Р(Н3) = 0,2
	P( /H3) = 0,8	P(H3 ) = 0,2× 0,8 = 0,16

 

Ответ. Вероятность активного экономического роста при условии, что доллар подорожает,

P(H_i/A) =0,467

 

Пример 3.3. В каждой из двух урн содержится 6 черных и 4 белых шара. Из первой урны во вторую наудачу переложен один шар.

1. Найти вероятность того, что шар, извлеченный из второй урны после перекладывания, окажется черным?

2. Предположим, что шар, извлеченный из второй урны после перекладывания, оказался черным. Какова тогда вероятность того, что из первой урны во вторую был переложен белый шар?

Решение. Определим события:

А - “шар, извлеченный из второй урны - черный”. Оно может произойти только вместе с одной из гипотез:

Н₁ - “из 1-й урны во 2-ю урну переложили черный шар” и

Н₂ - “из 1-й урны во 2-ю урну переложили белый шар”.

Используя классическое определение вероятностей, определим вероятности гипотез:

P(H₁) = 6/10; P(H₂) = 4/10.

и условные вероятности события А.

После перекладывания во второй урне окажется 11 шаров. Если из первой урны во вторую переложили черный шар, то во второй урне окажется 7 черных и 4 белых шаров.

Тогда P(A/H₁) = 7/11.

Если из первой урны во вторую переложили белый шар, то во второй урне окажется 6 черных и 5 белых шаров.

Тогда P(A/H₂) = 6/11.

Гипотезы образуют полную группу, сумма их вероятностей равна 1. Рассмотрим событие А - это (или Н₁А или Н₂А). События Н₁А и Н₂А - несовместные попарно, так как события Н₁ и Н₂ - несовместны.

События Н₁ и А, Н₂ и А - зависимые.

1. Вышеизложенное позволяет применить для определения вероятности события А и ответа на первый вопрос формулу полной вероятности (3.1):

P(A)=P(H₁)P(A/H₁) + P(H₂)P(A/H₂)=6/10 7/11 + 4/106/11 = 0,6.

Это же решение можно оформить в рабочей таблице:

 

Гипотезы Hi	P(Hi)	P(A/Hi)	P(Hi) P(A/Hi)
H1 - “из 1-й урны во 2-ю урну переложили черный шар”	6/10	7/11	42/110
H2- “из 1-й урны во 2-ю урну переложили белый шар”	4/10	6/11	24/110
S	1,00	-	0,6

 

Ответ. Вероятность того, что шар, извлеченный из второй урны после перекладывания, окажется черным составляет 0,6.

 

2. Во второй части задачи предполагается, что событие А уже произошло, т.е. шар, извлеченный из второй урны, оказался черным. Требуется найти уточненную (послеопытную, апостериорную) вероятность второй гипотезы, т.е. необходимо найти вероятность того, что из первой урны во вторую был переложен белый шар при условии, что шар, извлеченный из второй урны после перекладывания, оказался черным.

Р(Н₂/А) -?

Для определения искомой вероятности воспользуемся формулой Байеса (3.2):

 

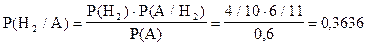
Мы можем получить тот же результат при помощи таблицы:

 

Гипотезы Hi	Априорные вероятности P(Hi)	Условные вероятности P(A/Hi)	Совместные вероятности P(A Hi)	Апостериорные вероятности P(Hi/A)
H1	6/10	7/11	42/110=0,3818	0,3818/0,6 = 0,6364
H2	4/10	6/11	24/110=0,2182	0,2182/0,6 = 0,3636
	1,00	-	0,6

 

Ответ. Вероятность того, что из первой урны во вторую был переложен белый шар при условии, что шар, извлеченный из второй урны после перекладывания, оказался черным, составляет 0,3636.

Задачи к теме 3

 

 

1. Руководство компании выяснило, что в среднем 85% сотрудников, отправленных на стажировку по применению новых информационных технологий, успешно завершают курс обучения. В дальнейшем из них 60% активно применяют в работе полученные знания. Среди тех сотрудников, которые не смогли успешно завершить обучение новые информационные технологии успешно применяют лишь 10%. Если случайно выбранный сотрудник компании активно применяет новые информационные технологии, то какова вероятность того, что он успешно прошел стажировку?

 

2. Агент по недвижимости пытается продать участок земли под застройку. Он полагает, что участок будет продан в течение ближайших шести месяцев с вероятностью 0,85, если экономическая ситуация в регионе не будет ухудшаться. Если же экономическая ситуация будет ухудшаться, то вероятность продать участок составит 0,4. Экономист, консультирующий агента полагает, что с вероятностью, равной 0,6, экономическая ситуация в регионе в течение следующих шести месяцев будет ухудшаться. Чему равна вероятность того, что участок будет продан в течение ближайших шести месяцев?

3. Судоходная компания организует средиземноморские круизы в течение летнего времени и проводит несколько круизов в сезон. Поскольку в этом виде бизнеса очень высокая конкуренция, то важно, чтобы все каюты зафрахтованного под круизы корабля были полностью заняты туристами, тогда компания получит прибыль. Эксперт по туризму, нанятый компанией, предсказывает, что вероятность того, что корабль будет полон в течение сезона, равна 0,87, если доллар не подорожает по отношению к рублю, и с вероятностью - 0,64, если доллар подорожает. По оценкам экономистов, вероятность того, что в течение сезона доллар подорожает по отношению к рублю, равна 0,1. Чему равна вероятность того, что билеты на все круизы будут проданы?

 

4. Исследованиями маркетологов установлено, что мужчины и женщины по-разному реагируют на рекламу средств бытовой химии. Результаты исследований показали, что 64% женщин позитивно реагируют на такую рекламу, считая что она дает полезную информацию о новинках в этой сфере, в то время как 48% мужчин реагируют на подобную рекламу негативно. 12 женщин и 8 мужчин заполнили анкету, в которой оценили новую рекламу средств бытовой химии. Случайно извлеченная анкета содержит негативную реакцию. Чему равна вероятность того, что её заполняла женщина?

5. Компьютерная фирма разработала программу автоматизации учета в кафе и ресторанах. Рекламные материалы были разосланы в крупнейшие кафе и рестораны города, которые составляют 70% от общего числа предприятий питания города. Закупили программу 40% кафе и ресторанов, которые получили рекламные материалы и 15% не получавших ее. Какова вероятность того, что случайно выбранное кафе, заказало новую программу автоматизации учета?

 

6. Экспортно-импортная фирма собирается заключить контракт на поставку сельскохозяйственного оборудования в одну из развивающихся стран. Если основной конкурент фирмы не станет одновременно претендовать на заключение контракта, то вероятность получения контракта оценивается в 0,55; в противном случае - в 0,35. По оценкам экспертов компании вероятность того, что конкурент выдвинет свои предложения по заключению контракта, равна 0,30. Чему равна вероятность заключения контракта?

7. Сотрудники отдела маркетинга полагают, что в ближайшее время ожидается рост спроса на продукцию фирмы. Вероятность этого они оценивают в 0,72. Консультационная фирма, занимающаяся прогнозом рыночной ситуации, подтвердила предположение о росте спроса. Положительные прогнозы консультационной фирмы сбываются с вероятностью 0,93, а отрицательные - с вероятностью 0,96. Какова вероятность того, что рост спроса действительно произойдет?

 

8. Из числа авиалиний некоторого аэропорта 70% - местные, 20% - по СНГ и 10% - в дальнее зарубежье. Среди пассажиров местных авиалиний 60% путешествуют по делам, связанным с бизнесом, на линиях СНГ таких пассажиров 50%, на международных - 90%. Из прибывших в аэропорт пассажиров случайно выбирается один. Чему равна вероятность того, что он бизнесмен?

 

9. Аудитор осуществляет проверку фирмы. В ходе работы у него накопилось 2 стопы бухгалтерских документов. В первой стопе содержит из 67 документов7 содержат ошибки, а во второй стопе из 45 документов 4 документа с ошибками. Случайно был переложен один документ из первой стопы во вторую. Какова вероятность того, что документ, извлеченный из второй стопы, содержит ошибку?

 

10. Компьютерная фирма продает мониторы 4 марок. При этом известно, что мониторы Sony составляют 24% от продаж, Panasonic-28%, LG – 16%, Samsung-32%. Вероятность неполадок в первый год работы для мониторов Sony составляет 0,01, Panasonic-0,02, LG – 0,03, Samsung-0,02. Какова вероятность неполадок в первый год работы случайно выбранного монитора?

 

11. При слиянии акционерного капитала двух фирм аналитики фирмы, получающей контрольный пакет акций, полагают, что сделка принесет успех с вероятностью равной 0,65, если председатель совета директоров поглощаемой фирмы выйдет в отставку; если он откажется, то вероятность успеха равна 0,3. Предполагается, что вероятность ухода в отставку председателя составляет 0,7. Чему равна вероятность успеха сделки?

12. На АЭС установлена система аварийной сигнализации. Когда возникает аварийная ситуация, звуковой сигнал срабатывает с вероятностью 0,999. Звуковой сигнал может сработать случайно и без аварийной ситуации с вероятностью 0,002. Реальная вероятность аварийной ситуации равна 0,004. Предположим, что звуковой сигнал сработал. Чему равна вероятность того, что это случилось в условиях реальной аварийной ситуации?

13. Нефтеразведочная экспедиция проводит исследования для определения вероятности наличия нефти на месте предполагаемого бурения скважины. Исходя из результатов предыдущих исследований, нефтеразведчики считают, что вероятность наличия нефти на проверяемом участке, равна 0,55. На завершающем этапе разведки проводится сейсмический тест, который имеет определенную степень надежности: если на проверяемом участке есть нефть, то тест укажет на нее в 92% случаев; если нефти нет, то в 14% случаев тест может ошибочно указать на ее наличие. Сейсмический тест указал на присутствие нефти. Чему равна вероятность того, что запасы нефти на этом участке существуют реально?

 

14. Вероятность того, что новый товар будет пользоваться спросом на рынке, если конкурент не выпустит в продажу аналогичный продукт, равна 0,58. Вероятность того, что товар будет пользоваться спросом при наличии на рынке конкурирующего товара 0,32. Вероятность того, что конкурирующая фирма выпустит аналогичный товар на рынок в течение интересующего нас периода 0,24. Чему равна вероятность того, что товар будет иметь успех?

 

15. Вероятность того, что клиент банка не вернет заем в период экономического роста, равна 0,06, а в период экономического кризиса - 0,23. Предположим, вероятность того, что начнется период экономического роста, равна 0,79. Чему равна вероятность того, что случайно выбранный клиент банка не вернет полученный кредит?

 

16. Экономист-аналитик условно подразделяет экономическую ситуацию в стране на “хорошую”, “посредственную” и “плохую” и оценивает их вероятности для данного момента времени в 0,25, 0,60 и 0,15 соответственно. Некоторый индекс экономического состояния возрастает с вероятностью 0,7, когда ситуация “хорошая”; с вероятностью 0,2, когда ситуация “посредственная”, и с вероятностью 0,1, когда ситуация “плохая”. Пусть в настоящий момент индекс экономического состояния возрос. Чему равна вероятность того, что экономика страны на подъеме?

 

17. Керамическая плитка одной марки, цвета и размера выпускается двумя цехами завода: первый цех выпускает 60% плитки, а второй 40%. Причем известно, что 8% продукции первого цеха имеют дефекты, тогда как этот же показатель для второго цеха равен 5%. Случайно взятая плитка имеет дефект. Чему равна вероятность того, что она выпущена первым цехом?

18. Опрос показал, что из 26 студентов, обучающихся в первой группе 18 ростовчан, а остальные живут в других городах, во второй группе 17 студентов-ростовчан, а остальные 10 живут в других городах. Из второй группы в первую был переведен один студент. После перевода один студент первой группы был вызван в деканат и оказалось, что это студент ростовчанин. Какова вероятность того, что из второй группы в первую был переведен студент-ростовчанин?

19. Страховая компания делит, водителей, заключивших договор автокаско на следующие группы риска: 1 группа – низкий риск; 2 группа - средний; 3 группа – высокий риск. Среди клиентов страховой компании 25% - первой группы; 65% - второй группы; 10% - третьей группы. Вероятность того, что страховое событие произойдет и страховая компания будет вынуждена выплатить страховое возмещение для первой группы риска оценивается как 0,1; для второй группы – 0,2; для третьей – 0,3. Какова вероятность того, что случайно выбранный клиент, получивший страховое возмещение, относится к группе среднего риска?

20. Работа сотрудников торгового зала супермаркета организована в две смены. В первой смене работают 5 мужчин и 7 женщин, во второй смене – 9 мужчин и 10 женщин. Из второй смены в первую был переведен один сотрудник. Клиент супермаркета пригласил сотрудника торгового зала для консультации. Консультировал клиента сотрудник – мужчина. Какова вероятность того, что из второй смены в первую была переведена женщина?