ѕусть имеетс€ множество N элементов, из которых ћ элементов обладают некоторым признаком A. »звлекаетс€ случайным образом без возвращени€ n элементов. “ребуетс€ найти веро€тность того, что из них m элементов обладают признаком A. »скома€ веро€тность (завис€ща€ от N, M, n, m) определ€етс€ по формуле:
 (4.15)
(4.15)
≈сли по формуле (4.15) вычислить веро€тности дл€ всех возможных значений m, то полученный р€д распределени€ называетс€ гипергеометрическим законом распределени€ (таблица 4.5):
“аблица 4.5
| M | ... | n | |||
| P(X=m) | 
| 
| 
| ... | 
|
ћатематическое ожидание и дисперси€ случайной величины m, распределенной по гипергеометрическому закону, определ€ютс€ формулами:
 (4.16)
(4.16)
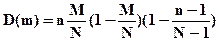 (4.17)
(4.17) 
ѕример 4.1 »звестно, что в определенном городе 20% горожан предпочитают добиратьс€ на работу личным автотранспортом. —лучайно выбраны 4 человека.
а) —оставьте р€д распределени€ числа людей в выборке, предпочитающих добиратьс€ на работу личным автотранспортом, и постройте его график.
б) Ќайдите числовые характеристики этого распределени€;
в) Ќапишите функцию распределени€ числа людей в выборке, предпочитающих добиратьс€ на работу личным автотранспортом и постройте еЄ график.
г) „ему равна веро€тность того, что среди 4-х случайно отобранных человек не будет ни одного, предпочитающего добиратьс€ на работу личным автотранспортом?
д) „ему равна веро€тность того, что среди 4-х случайно отобранных людей окажетс€ хот€ бы один, предпочитающий добиратьс€ на работу личным автотранспортом?
е) „ему равна веро€тность того, что среди 4-х случайно отобранных человек будет не больше двух, предпочитающих добиратьс€ на работу личным автотранспортом?
–ешение. ¬ качестве случайной величины в данной задаче выступает число людей в выборке, предпочитающих добиратьс€ на работу личным автотранспортом. ќбозначим ее через X.
ѕеречислим все возможные значени€ случайной величины ’: 0, 1, 2, 3, 4.
¬еро€тность того, что каждый из отобранных людей предпочитает добиратьс€ на работу личным автотранспортом, - посто€нна и равна 0,2 (p = 0,2). ¬еро€тность противоположного событи€, т.е. того, что каждый из отобранных людей предпочитает добиратьс€ на работу не личным автотранспортом, а как-то иначе - также посто€нна и составл€ет 0,8 (q = 1 - p = 1 0,2 = 0,8).
¬се 4 испытани€ - независимы, т.е. веро€тность того, что каждый из отобранных людей предпочитает добиратьс€ на работу личным автотранспортом, не зависит от того, каким способом предпочитает добиратьс€ на работу любой другой человек из числа случайно отобранных.
ќчевидно, что случайна€ величина ’ - подчин€етс€ биномиальному закону распределени€ веро€тностей с параметрами n=4 и p=0,2.
»так, по условию задачи: n = 4; p = 0,2; q = 0,8; X = m.
а) „тобы построить р€д распределени€, необходимо вычислить веро€тности того, что случайна€ величина примет каждое из своих возможных значений и записать полученные результаты в таблицу.
–асчет искомых веро€тностей осуществл€етс€ по формуле Ѕернулли.
|
|
|

ѕодставим в эту формулу данные задачи:





ѕолучим р€д распределени€ числа людей в выборке, предпочитающих добиратьс€ на работу личным автотранспортом:
| ’ | |||||
| – | 0,4096 | 0,4096 | 0,1536 | 0,0256 | 0,0016 |
“ак как все возможные значени€ случайной величины образуют полную группу событий, то сумма их веро€тностей должна быть равна 1.
ѕроверка: 0,4096 + 0,4096 + 0,1536 + 0,0256 + 0,0016 = 1.
¬место р€да распределени€ дискретна€ случайна€ величина может быть задана графически многоугольником (полигоном) распределени€ (рис. 4.3).

–ис. 4.3.
б) Ќайдем основные числовые характеристики распределени€ данной случайной величины: математическое ожидание, дисперсию и среднее квадратическое (стандартное) отклонение.
ћатематическое ожидание любой дискретной случайной величины может быть рассчитано по формуле (4.4):
 = 0 × 0,4096 + 1 × 0,4096 + 2 × 0,1536 + 3 × 0,0256 +4 × 0,0016 = =0,8 (чел.)
= 0 × 0,4096 + 1 × 0,4096 + 2 × 0,1536 + 3 × 0,0256 +4 × 0,0016 = =0,8 (чел.)
¬месте с тем, ввиду того, что в данном случае речь идет о математическом ожидании частоты, дл€ его расчета можно воспользоватьс€ более простой формулой (4.10):
M(X = m) = np = 4 × 0,2 = 0,8 (чел.)
–ассчитаем дисперсию числа человек, предпочитающих добиратьс€ на работу личным автотранспортом, среди 4-х отобранных. ƒисперси€ любой дискретной случайной величины может быть рассчитана по формуле:
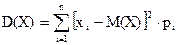 = (0 - 0,8)2 × 0,4096 +(1 - 0,8)2 × 0,4096 +(2 - 0,8)2 × 0,1536 + (3 - 0,8)2 × 0,0256 + (4 - 0,8)2 × 0,0016 = 0,64 (кв.ед).
= (0 - 0,8)2 × 0,4096 +(1 - 0,8)2 × 0,4096 +(2 - 0,8)2 × 0,1536 + (3 - 0,8)2 × 0,0256 + (4 - 0,8)2 × 0,0016 = 0,64 (кв.ед).
¬ данном случае речь идет о дисперсии частоты, а еЄ можно найти по формуле (4.11):
D(X = m) = npq = 4 × 0,2 × 0,8 = 0,64 (кв.ед)
–ассчитаем среднее квадратическое отклонение числа людей в выборке, предпочитающих добиратьс€ на работу личным автотранспортом. —реднее квадратическое отклонение рассчитываетс€ по формуле:

в) ƒискретную случайную величину можно задать функцией распределени€:

где дл€ каждого значени€ х суммируютс€ веро€тности тех значений xi, которые лежат левее точки х.
«ададим функцию распределени€ дискретной случайной величины применительно к условию данной задачи:
 .
.
ƒл€ построени€ графика функции распределени€ веро€тностей дискретной случайной величины необходимо рассчитать кумул€тивные (накопленные) веро€тности, соответствующие значени€м случайной величины. јлгоритм их расчета вытекает из смысла функции распределени€:
F(Xi) = P(X1) + P(X2) +... + P(X i -2) + P(X i -1)
Ёта формула справедлива дл€ всех F(Xi), кроме F(X0). “ак как по определению функци€ распределени€ определ€ет веро€тность того, что случайна€ величина примет значение, меньшее заданного, пон€тно, что веро€тность того, что случайна€ величина примет значение, не более минимального, равна 0:
F(X0) = 0.
–ассчитаем значени€ F(х):

Ёти данные можно представить и в виде таблицы:
| ’ | x £ 0 | 0 < x £ 1 | 1 < x £ 2 | 2 < x £ 3 | 3 < x £ 4 | x > 4 |
| F(x) | 0.4096 | 0.8192 | 0.9728 | 0.9984 |
√рафик функции распределени€ веро€тностей дискретной случайной величины имеет ступенчатый вид. —качки равны веро€тност€м, с которыми случайна€ величина принимает возможные значени€ (рис.4.4).






