При моделировании приходится формализовать связи исследуемого явления (процесса), из-за чего возможна потеря некоторой информации об объекте. Иногда некоторые связи не учитываются. В то же время основное требование к математической модели заключается в ее пригодности для решения поставленной задачи и адекватности процессу. Регрессионную модель называют адекватной, если предсказанные по ней значения у согласуются с результатами наблюдений. Так, построив модель в виде линейного уравнения регрессии, мы хотим, в частности, убедиться, что никакие другие модели не дадут значительного улучшения в описании предсказания значений у. В основе процедуры проверки адекватности модели лежат предположения, что случайные ошибки наблюдений являются независимыми, нормально распределенными случайными величинами с нулевыми средними значениями и одинаковыми дисперсиями.
Сформулируем нуль-гипотезу Н0: "Уравнение регрессии адекватно".
Альтернативная гипотеза Н1: "Уравнение регрессии неадекватно".
Для проверки этих гипотез принято использовать F-критерий Фишера.
При этом общую дисперсию (дисперсию выходного параметра) S y2 cравнивают с остаточной дисперсией Sуост2.
Напомним, что
(2.1)
где l=k+1 – число членов аппроксимирующего полинома, а k – число факторов. Так, например, для линейной зависимости k=1, l=2.
В дальнейшем определяется экспериментальное значение F-критерия
(2.2)
который в данном случае показывает, во сколько раз уравнение регрессии предсказывает результаты опытов лучше, чем среднее 
Если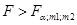 
, то уравнение регрессии адекватно. Чем больше значение 
превышает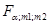 
для выбранного α и числа степеней свободы m1=n-1, m2=n-l, тем эффективнее уравнение регрессии.
Рассмотрим также случай, когда в каждой i-й точке xi для повышения надежности и достоверности осуществляется не одно, а m* параллельных измерений (примем для простоты, что m* одинаково для каждого фактора). Тогда число экспериментальных значений величины у составит nΣ=n⋅m*.
В этом случае оценка адекватности модели производится следующим образом:
1) определяется 
– среднее из серии параллельных опытов при x=xi, где yij – значение параметра у при x=xi в j-м случае;
2) рассчитываются значения параметра 
по уравнению регрессии при x=xi;
3) рассчитывается дисперсия адекватности
где n – число значений xi; l – число членов аппроксимирующего полинома (коэффициентов bi), для линейной зависимости l=2;
4) определяется выборочная дисперсия Y при x=xi:
5) определяется дисперсия воспроизводимости
Число степеней свободы этой дисперсии равно m=n(m*-1);
6) определяется экспериментальное значение критерия Фишера
7) определяется теоретическое значение этого же критерия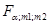
где m1=n-l; m2= n (m*-1);
8) если 
, то уравнение регрессии адекватно, в противном случае – нет.
