В качестве факторов можно выбирать только контролируемые и управляемые переменные, т.е. такие, которые исследователь может поддерживать постоянными в течение каждого опыта на заданном уровне. В число факторов должны быть включены параметры процесса, оказывающие наиболее сильное влияние на функцию отклика. Необходимо заметить, что, несмотря на всю заманчивость и очевидные преимущества активного спланированного эксперимента перед пассивным, в его применении имеется целый ряд трудностей, связанных с определенными ограничениями на его реализацию. Важнейшим условием применимости этого подхода является управляемость процессов по каждому из выбранных факторов, т.е. возможность независимого изменения каждого из этих факторов и поддержания его на заданном уровне в период проведения опытов.
Для каждого фактора необходимо указать тот интервал изменения параметров, в пределах которого ставится исследование. Для этого на основе априорной информации устанавливаются ориентировочные значения факторов x10, x20,..., xi0,..., xk0. Этой комбинации значений факторов соответствует точка в многомерном факторном пространстве, которая принимается за исходную точку. Координаты этой точки принимаются за основной (нулевой) уровень.
Интервалом варьирования факторов называется некоторое число (каждое для соответствующего фактора), прибавление которого к основному уровню дает верхний, а вычитание – нижний пределы. Для упрощения записи условий эксперимента и обработки экспериментальных данных масштабы по осям выбираются так, чтобы верхний уровень составлял +1, нижний -1, а основной – 0.
Для факторов с непрерывной областью определения это достигается с помощью преобразования (кодирования) факторов:
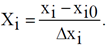(1.7)
В теории планирования экспериментов показано, что минимально необходимое число уровней факторов на единицу больше порядка уравнения.
Планирование эксперимента
Рассмотрим сначала частный случай, когда функция отклика линейно зависит от трех независимых факторов. Уравнение регрессии в этом случае имеет вид (1.9), а план эксперимента представлен в табл. 1.
Таблица 1 - Таблица полного факторного эксперимента для трех факторов
| Номер опыта | План | Результат yj | |||||||
| x0 | x1 | x2 | x3 | x1x2 | x1x3 | x2x3 | x1x2x3 | ||
| +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | y1 | |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | y2 | |
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | y3 | |
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | y4 | |
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | y5 |
Продолжение таблицы 1
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | y6 | |
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | y7 | |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | y8 |
Здесь добавлен столбец фиктивной переменной х0, нужный для оценки свободного члена b0. После реализации плана получают 8 уравнений с 8 неизвестными, их решение и даст оценку всех 8 коэффициентов регрессии b0, b1,..., b3, b12,..., b123.
План, в котором число опытов равно числу определяемых коэффициентов, называется насыщенным.
Заметим, что мы использовали все точки с "крайними" координатами, т.е. ±1, или, говоря другими словами, все возможные комбинации выбранных уровней. В самом деле, всех возможных комбинаций 2k=8 (k – число факторов), и мы все их использовали. Если эксперименты проводятся только на двух уровнях (при двух значениях факторов) и при этом в процессе эксперимента осуществляются все возможные неповторяющиеся комбинации из k факторов, то постановка опытов по такому плану носит название полного факторного эксперимента (ПФЭ) или 2k.
Иными словами, полный факторный эксперимент (ПФЭ) — это эксперимент, реализующий все возможные неповторяющиеся комбинации уровней независимых факторов.
| Рисунок 1.1 – Геометрическое изображение ПФЭ |
Кодированный план геометрически может быть интерпретирован в виде куба, восемь вершин которого представляют собой восемь экспериментальных точек (рис.1.1).
При числе факторов k=2 построение матрицы ПФЭ не вызывает затруднений, при увеличении же числа факторов возникает необходимость в некоторых специальных приемах построения матрицы.
Первый прием основан на чередовании знаков. В первом столбце (для x1) знаки чередуются поочередно. Во втором (для х2) — через 2, в третьем (для х3) — через 4 и т.д. по степеням двойки 2k. Этот подход и использован при составлении плана, представленного в табл.1.
Второй прием основан на последовательном достраивании матрицы. Для этого при добавлении нового фактора необходимо повторить комбинации уровней исходного плана — сначала при значениях нового фактора на верхнем уровне, а затем — на нижнем.
Матрица ПФЭ обладает следующими свойствами:
1) свойство симметричности: алгебраическая сумма элементов вектор-столбца каждого фактора равна нулю (за исключением столбца, соответствующего свободному члену):
(1.8)
где i – номер фактора; j – номер опыта;
2) свойство нормирования: сумма квадратов элементов каждого столбца равна числу опытов:
(1.9)
3) свойство ортогональности: скалярное произведение всех вектор-столбцов (сумма почленных произведений элементов любых двух векторстолбцов матрицы) равно нулю:
(1.10)
Планы, для которых выполняется свойство 3, называют ортогональными. Благодаря этому свойству резко уменьшаются трудности, связанные с расчетом коэффициентов уравнения регрессии.
Поскольку результаты наблюдений отклика носят случайный характер, приходится в каждой точке плана проводить не один, а m* параллельных опытов (обычно m*=2÷4), осреднение результатов которых, как уже отмечалось, дает возможность уменьшить погрешности оценки истинного значения отклика в 
раз.
В каждой серии экспериментов их последовательность рандомизируется, т.е. с помощью таблиц случайных чисел определяется случайная последовательность реализации экспериментов. Рандомизация дает возможность свести эффект некоторого случайного фактора к случайной погрешности. Это позволяет в определенной степени исключить предвзятость и субъективизм исследователя.
