МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению курсовой работы
по дисциплине «Инженерный эксперимент» для студентов направления подготовки 13.04.01 «Теплоэнергетика
и теплотехника» (программа магистерской подготовки «Промышленная теплоэнергетика») очной формы обучения
Воронеж 2015
Составители: канд. техн. наук В.Г. Стогней,
. канд. техн. наук П.А. Солженикин,
. канд. техн. наук В.В. Черниченко
УДК 69.162.2.012-52
Методические указания к выполнению курсовой работы по дисциплине «Инженерный эксперимент» для студентов направления подготовки 13.04.01 «Теплоэнергетика и теплотехника» (программа магистерской подготовки «Промышленная теплоэнергетика») очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. В.Г. Стогней, П.А. Солженикин,
В.В. Черниченко. Воронеж, 2015. 44 с.
В методических указаниях приводятся основные теоретические сведения по планированию экспериментов, а также описание методов обработки их результатов.
Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2003 и содержатся в файле Мет. указ. ИЭ.doc.
Табл. 6. Ил. 6. Библиогр.: 13 назв.
Рецензент профессор В.Ю. Дубанин
Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. А.В. Бараков
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
© ФГБОУ ВПО «Воронежский
государственный технический
университет», 2015
Методы планирования экспериментов
Основные определения и понятия
Ранее мы рассматривали пассивный эксперимент, и математическая статистика использовалась, в частности, при обработке экспериментальных данных. На стадии постановки эксперимента она не применялась. При активном же эксперименте математическая статистика используется уже на стадии постановки и планирования эксперимента.
Пассивный эксперимент предусматривает накопление информации “в режиме нормальной эксплуатации", но это требует много времени и затрат. Поэтому предлагается "не ждать милостей от природы", а активно вмешиваться в ход технологического процесса: «разбалтывать» («покачивать») его тихонько, но целенаправленно, и быстро накапливать при этом информацию. Программа покачивания как раз и задается планом. Сам метод планирования может изменяться в зависимости от вида задачи, но принцип покачивания остается.
Теория планирования эксперимента началась с работ знаменитого английского ученого Р. Фишера в 30-х годах XX столетия, использовавшего ее для решения агробиологических задач. В дальнейшем это направление было развито в пятидесятых годах в США Дж. Боксом и его сотрудниками. Отечественные ученые также внесли большой вклад в развитие теории эксперимента, предложив ряд новых методов, а инженеры-исследователи все шире применяют эти методы на практике.
Под математической теорией планирования эксперимента будем понимать науку о способах составления экономичных экспериментальных планов, которые позволяют извлекать наибольшее количество информации об объекте исследования, о способах проведения эксперимента, о способах обработки экспериментальных данных и их использования для оптимизации производственных процессов, а также инженерных расчетов. Принятая терминология — это либо перевод терминов с английского, либо просто их перенос в оригинале, и это необходимо иметь в виду при чтении литературы по теории планирования экспериментов.
Истинный вид функции отклика 
до эксперимента чаще всего неизвестен, в связи с чем для математического описания поверхности отклика используют уравнение
(1.1)
где xi, xu – переменные факторы при i=1,..., k; u=1,..., k; i≠u;
– коэффициенты.
Это уравнение является разложением в ряд Тейлора неизвестной функции отклика в окрестности точки с xi =xi0 .
На практике по результатам эксперимента производится обработка данных по методу наименьших квадратов. Этот метод позволяет найти оценку b коэффициентов β, и данный полином заменяется уравнением вида
(1.2)
которое является регрессионной моделью (моделью регрессионного анализа). В этом выражении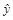 
означает модельное, т.е. рассчитываемое по уравнению модели, значение выхода. Коэффициенты регрессии определяются экспериментально и служат для статистической оценки теоретических коэффициентов, т.е.
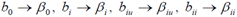
В регрессионной модели члены второй степени xixu, xi2 характеризуют кривизну поверхности отклика. Чем больше кривизна этой поверхности, тем больше в модели регрессии членов высшей степени. На практике чаще всего стремятся ограничиться линейной моделью.
Последовательность активного эксперимента заключается в следующем:
1) разрабатывается схема проведения исследований, т.е. выполняется планирование эксперимента. При планировании экспериментов обычно требуется с наименьшими затратами и с необходимой точностью либо построить регрессионную модель процесса, либо определить его оптимальные условия;
2) осуществляется реализация опыта по заранее составленному исследователем плану, т.е. осуществляется сам активный эксперимент;
3) выполняется обработка результатов измерений, их анализ и принятие решений.
Таким образом, планирование эксперимента – это процедура выбора условий проведения опытов, их количества, необходимых и достаточных для решения задач с поставленной точностью.
Использование теории планирования эксперимента обеспечивает:
1) минимизацию, т.е. предельное сокращение необходимого числа опытов;
2) одновременное варьирование всех факторов;
3) выбор четкой стратегии, что позволяет принимать обоснованные решения после каждой серии опытов;
4) минимизацию ошибок эксперимента за счет использования специальных проверок.
Для иллюстрации некоторых из этих положений воспользуемся ставшим уже классическим примером из книги В.В. Налимова, Т.И. Голиковой.
Планирование первого порядка
Под планами первого порядка понимают такие планы, которые позволяют провести эксперимент для отыскания уравнения регрессии, содержащего только первые степени факторов и их произведения:
(1.3)
Планы второго порядка позволяют провести эксперимент для отыскания уравнения регрессии, содержащего и вторые степени факторов:
(1.4)
Нахождение уравнения регрессии методом планирования экспериментов состоит из следующих этапов:
− выбор основных факторов и их уровней;
− планирование и проведение собственно эксперимента;
− определение коэффициентов уравнения регрессии;
− статистический анализ результатов эксперимента.
На первой стадии исследования обычно принимают полином первой степени. Так, для трехфакторной задачи теоретическое уравнение регрессии имеет вид
(1.5)
Уравнение регрессии, получаемое на основании результатов эксперимента, в отличие от приведенного теоретического уравнения, имеет вид
(1.6)
где коэффициенты регрессии b0, b1,..., b3,..., b123 являются оценками для теоретических коэффициентов регрессии, т.е.
Члены, содержащие произведения х1х2; х2х3 и т.д., называют членами, отражающими попарное взаимодействие факторов, члены вида х1х2х3 — членами тройного взаимодействия.
