Минимизация функционального представления

МНОЖЕСТВ.

Определим функцию от фрагментов, являющихся множествами. Функцией будем называть взаимооднозначное отображение элементов группы множеств А_i в элементы множества С. Если каждому элементу С соответствует некоторый элемент А_i, такую функцию называют всюду значимой

С = f (A_i)

f – функция переводит элементы A_i во множество С.

Если пересечение множеств обозначать как функциональную операцию Р, то

Р (А,В) = АВ

На единичном множестве 1 заданы множества А,В,С. В этом случае с помощью известной операции над множествами переводим исходное множество в какое-либо другое.

f (А,В,С) = АВС È А С È В È È АВ È AС È С È В;

Записанное выражение назовем формулой. Определим сложность формулы, как количество, содержащихся в ней исходных множеств. Для приведенного примера сложность =20. При аналазе формул первым вопросом является: «Можно ли уменьшить сложность формулы?» Сделаем это на примере применяя законы дистрибутивности и поглощения

f(А,В,С) = АВС È А È В È È А(В È С) È (В È С) =

= АВС È А È B È È В È С = ВÈ А È È С =

= È В È С = È =1

f(А,В,С) = АС È С È ВС È АВС È АВ È В = АС È С È В È АВ =

=В È АС È С;

Или:

F(А,В,С) = АС È С È ВС È АВС È АВ È В = АС È С È ВС È АВ È È В = АС È С È ВС È В = С È В

Как видно из примеров минимизация одних и тех же функций может дать разные результаты при применении одних и тех же законов.

 

СТАНДАРТНЫЕ ФОРМЫ ПРЕДСТАВЛЕНИЙ ФОРМУЛ

МНОЖЕСТВ.

На 1 определении М₁,М₂,М₃ совокупность М_i назовем порожд-ми множествами пространства и определим М_i по универсальной формуле:

М_i ; d_i =1;

M_i^di = d_i={0;1}

_i ; d_i =0;

Мi = i = {0,1}

Mi; i=0;

 

M_i, d_i – первичный термом

K_i = _i^di - конституентой

n - число порожденных множеств.

Перечислим все конституенты нашего примера:

К₀ = _{1 2 3} К₁ = _{1 2}М₃ К₂ = ₁М_{2 3} К₃ = ₁М₂М₃

К₄ = М_{1 2 3} К₅ = М_{1 2}М₃ К₆ = М₁М_{2 3} К₃ = М₁М₂М₃

 

Очевидно, что каждой приведенной коституенте может быть сопоставлено двоичное трехразрядное число, причем каждый разряд будет равен d_i первичного терма:

К₀ = 000; К₁ = 001; К₂ = 010; К₄ =011; К₅ = 100; К₆ = 110; К₇ = 111.

Если учесть,что каждой конституенте длины П можно сопоставить n разр.

двоичное число, то общее количество конституент равно:

N = 2ⁿ

1) Выражения, заданные с помощью формул,могут быть упрощены.

2) Необходимые шаги для упрощения не всегда очевидны и сложность упрощения находится в прямой зависимости от числа аргументов в формуле.

3) Для упрощения выражения произв. вида и произв. количества аргументов необходимо использовать математический аппарат минимизации функций подмножеств.

Пересечение двух различных конституент - пустое множество.

Пересечение двух конституент – есть пересечение всех первичных термов их составляющих, если конституенты не равны, то найдется хотя бы 1 разряд с несовпадающими первичными термами.

Обозначим этот разряд через i.

M_i^di *M_i^di*= Æ

Объединение всех коституент,порожденных множествами M_i на универсальном множестве равно самому универсальному множеству:

I= (M_i È _i)

n=1 M₁, ₁ M₁+ ₁=I

 

n=k _j = I

С помощью конституент, образованных множествами M_i,можно представить исходное универсальное множество.

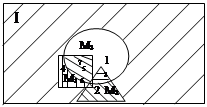
1. Проиллюстрируем на графическом примере:

(универсальное множество I, внутри М₁-квадрат, М₂-треугольник, М₃-круг).

 

В дополнение к рассматриваемым свойствам,рассмотрим сколько множеств на I можно образовать из конституент.

Для этого произвольному множеству сопоставим m-разрядное двоичное число,где m-длина конституент. При этом 0-отсутствие конституенты, 1-присутствует.

Так например, двоичному числу

01101001 соответствует множество, из объединенных 0,3,5,и 6 конституент.

Вместо двоичных чисел можно использовать их десятичный эквивалент:

d = 1+2³+2⁵+2⁶ = 1+8+32+64 = 40+ 65 = 105

Если любому, образованному из конституент, множеству соответствует m-разрядное двоичное число, то таких множеств может быть 2^m,а так как число конституент = 2ⁿ, где n-число образованных множеств,то общее число, которое образуется из конституент = 2^{2^n}

Для иллюстрации это количество -256.

Рассмотрев понятие конституент зададимся вопросом:»Как конституенты связаны с функциями от образующих множеств?»

МАТЕМАТИЧЕСКИЕ УТВЕРЖДЕНИЯ.

Множество M_i равно объединению всех конституент,содержащих M_i

Рассмотрим равенство:

I = _j-1

Возьмем пересечение левых и правых частей с M_i

Mi = _j-1M_i

Рассмотрим выражение К_j,M_i. Для него возможны два случая:

1.K_j не содержит в себе M_i, Ki*Mi = Æ

2.K_j Ì M_i, K_j*M_i =K_j

Следовательно, M_i можно представить в виде:

 

М_i = _l

 

k_l -конституенты,содержащие M_i.

ТЕОРЕМА.

Любая функция от порождающих множеств представима в виде объединения конституент.

Из аксиоматичного построения следует,что все операции представимы через операции объединения и отрицания.

Следовательно, достаточно доказать,что объединение порождающих множеств представимо через объединение конституент, а так же,что отрицание объединения конституент,так же представимо через объединение множеств.

Для доказательства рассмотрим объединение произвольно образованных множеств M_i и М_к.

Согласно утверждению (M_i È М_к),записывающихся в виде:

 

 

М_i È М_к = _j+ _l М_i È М_к = _j

при этом М – различно,так как различно число совпадающих конституент в представлениях множеств M_i иМ_к.

Остается доказать,что дополнения к объединению конституент в свою очередь есть объединение конституент.

Так как универсальльное множество является объединением всех конституент, ясно,что если взять объединение некоторых из них, то оставшиеся конституенты будут дополнительными к исходному объединению.

Рассмотрим пример:

Функция от множеств А,В,С

f(A,В,С) = А(В È ((С 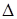А)\В)) = А(В È ((С È С )\В)) = А(В È (С È А) ) =

А(В È С È А ) = АВ È А = А È АВС È АВ

Из пересечения АВ получена АВС È С. Ясно,чтобы получит трех-разрядную конституенту, необходимо до термов АВ добавить С, а так как произв-но множество М:

М(С È ) = МС È М АВ = АВС È АВ

то просто получим из АВ трехразрядную конституенту.

Итак, любая функция от порождающих множеств, может быть представлена в виде объединения коституент и оно называется совершенной норм.Кантора (СНФК).

Если в представлении функции участвовали конституенты меньшей длины, то оно называется норм. формой Кантора (НФК).

Для получения РФК нужно минимизании СНФК любым (аналитическим, графическим,графо-аналитическим способом).

Назовем интервалами универсального пространства ранга n все коституенты длина l =1, n

Если какая-либо С₁ (интерв.) = С₂È С₃, то говорят что С₁ включает в себя С₂ и С₃ или С₁ покрывает С₂ и С₃

Из этого следует, что функция,представленная в СНФК равна:

f (A,В,С) = _j= _l

где C_l - интервалы,покрывающие все конституенты К_j .

Если рассмотреть предыдущий пример,то можно заметить,что f(А,В,С):

f (A,В,С) = АВ È А

где, АВ покрывает АВС и АВ , а втор. совпадает с А .

 

ГРАФИЧЕСКАЯ МИНИМИЗАЦИЯ ФУНКЦИИ ОТ

ТРЕХ ПЕРЕМЕННЫХ.

 

Введем геометрическое представление интервалов при n=3.

Для этого каждой из 8 конституент, сопоставив вершину трехмерного куба и двоичный эквивалент. При этом расположим вершины так,чтобы их двоичные представления отличались лишь в одном разряде.

 

 

Сопоставим коституенты с их двоичным эквивалентом:

000 – ; 001 – C; 010 – В ; 011 – ВС; 100 – А ;

101 – А С; 110 – АВ ; 111 – АВС.

Рассмотрим более сложные интервалы:

È В =

О – О, где — - отсутствие разряда

Геометрически - сопоставляется ребро соединения вершины 000 и 010.

Запишем соответствие ребер интервала:

-00 = ; -01 = С; -10 = В ;

0-0 = ; 0-1 = С; 1-0 = А ;

00- = ; 01- = В; 10- = А ;

-11 = ВС; 1-1 = АС; 11- = АВ.

По аналогии ребра конституенты можно объеденить в грань.

АВ È В È В È ВС = В

Соответствия граней:

--0 = ; --1 = С

-0- = ; -1- = В;

0-- = ; 1-- = А.

Для представления функции на кубе,участвующие интервалы выделяются.

111 110

 

 

_{101 100}

 

001 000

f(A,В,С) = С È В

111 B 110

В этом примере видно,что конституенты В и

ВС покрытые В

^{101 100} и В и АВ покрытые В можно покрыть одним

_{001 000} интервалом В.

f(A,В,С) = С È В

и так как сложность уменьшилась с трех до двух, была произведена минимизация функции.

 

МИНИМИЗАЦИЯ ФУНКЦИИ ТРЕХ ПЕРЕМЕННЫХ

ГРАФИЧЕСКИМ СПОСОБОМ.

f(M₁,М₂,М₃) = _{1 2}М₃ + ₁М₂М₃ + М₁М₂М₃ + М_{1 2 3}

111 110

 

 

_{101 100}

 

001 000

f(M₁,М₂,М₃) = ₁М₃ + М₂М₃ + М_{1 2 3}

 

МИНИМИЗАЦИЯ ФУНКЦИИ С ПОМОЩЬЮ КАРТ

КАРНО.

 

Графический способ минимизации удобен для трех,четырех переменных, а для функции пяти переменных и выше применение графического метода невозможно.

Поэтому для использования принципа этого метода для большеге количества переменных предложена модернизация.

Идея: развернуть куб на плоскости

_{000 001 011 010 000}

^{100 101 111 100 100}

Исходя из развертки куба, строится таблица:

М₁ М₂М_{3 00 01} М_{3 11 10}

1

М₁

М₂

 

 

Построенная таблица – карта КАРНО.

В ней отмечены конституенты,присутствующие в функции, подобно тому, как отмеченные вершины куба объеденены в ребра и грани.

Объед. и еден. карты (интервалы).

Объединение единиц в интнрвалы в карте иначе называют склеиванием.

Этапы заполнения карты КАРНО.

1. Все конституенты, присутствующие в функции заносятся в карту с помощью единиц в соответствующие клетки.

2. Выделяют интервалы на карте по следующим принципам:

а) в один интервал объединяют только соседние единицы по вертикали или горизонтали;

б) в один интервал можно объеденить 2^к единиц, где k=0,1,2,3,4,….

в) карта циклически замкнута по вертикали и горизонтали.

г) в выделенный интервал объединено максимально возможное количество единиц.

Всего на карте выделено 3 интервала, в каждый входят те минитермы в которых он полностью находится.

Запишем минимальную функцию:

f(M₁,М₂,М₃) = М₁М₃ + М₂М₃ + М_{1 2 3}

Пример:

Минимизировать функцию:

f(M₁,М₂,М₃)= _{1 2 3} + М_{1 2 3} + _{1 2} М₃ + М_{1 2} М₃ + М₁М₂М₃ +

+ ₁М_{2 3} + М₁М_{2 3}

 

_{00 01} М_{3 11 10}

1

М₁

М₂

f(M₁,М₂,М₃) = ₂ + М₁ + ₃

При правильном объединении функцию больше минимизировать невозможно.

Карта Карно для 4-х переменных:

М₁М₂ М₃М_{4 00 01 11 10}

00
					М2
11
					М1

^М 3

М₄

f(M₁,М₂,М₃) = М₁М₄ + М₂М₄ + _{1 2 4}

 

Пример:

f(M₁,М₂,М₃,М₄) (3,4,5,7,9,11,12,13 конституенты)

М₁М₂ М₃М_{4 00 01 11 10}

 

3 - 0011 4 - 0100 5 - 0101 7 - 0111 9 - 1001

11- 1011 12 - 1100 13 - 1101

f(M₁,М₂,М₃,М₄)= М_{2 3}+ ₁М₃М₄ +М_{1 2}М₄

 

 

Карты Карно для 5-ти переменных:

М₄ М₅

М₁М₂ М₃М₄М_{5 001} М_{3 011 010 110 111 101 100}

01
М2 11
М1 10

 

При выделении интервалов необходимо соблюдать дополнительные правила:

1) Все интервалы должны быть симметричны относительно исходных размеров карт;

2) Если 2 единицы находятся симметрично границы раздела они считаются соседними.

f(М₁,М₂,М₃,М₄,М₅) = М_{2 3} М₅ + М_{1 3} М₄ М₅ + М_{1 2} М₃М_{4 5}

f(М₁,М₂,М₃,М₄,М₅) = ₁ М_{2 3 4}М₅ + ₁ М_{2 3} М₄ М₅ +

+ М₁М_{2 3 4} М₅ + М₁ М_{2 3} М₄ М₅ + М_{1 2 3 4} М₅ +

+ М_{1 2 3} М₄ М₅ + ₁ М_{2 3} М_{4 5} + М₁ М_{2 3} М_{4 5} +

+ ₁М₂М₃ М_{4 5} + М₁ М₂М₃ М_{4 5} + М_{1 2}М₃ М₄ М₅ +

+ М_{1 2}М_{3 4} М₅

М₁М₂ М₃М₄М_{5 001 011 010 110 111 101 100}

 

f(М₁,М₂,М₃,М₄,М₅) = М_{2 3} М₅ + М₂ М_{4 5} + М_{1 2} М₅

 

Аппарат работы с картами и их преимущество.

 

1) Простота применения.

2) Наглядность расположения интервалов.

 

Недостатки:

1) Сложность работы возростает намного быстрее, чем увеличивается число элементов функции.

2) Трудоемкость алгоритмизации.

Исходя из недостатков следует, что для работы с функциями большего числа переменных нужны иные методы, причем они должны быть не графическими а аналитическими.

Для компьюторной технологии существует отличный от рассмотренного метода минимизации множеств,который называется метод Квайна.

МИНИМИЗАЦИЯ ФУНКЦИИ МЕТОДОМ КВАЙНА.

Максимальный интервал I_a, который не содержится ни в каком другом интервале I_a Ë I_к

где I_к - все интервалы функции, кроме I_a.

Рассмотрим функцию, заданную в СНФК:

N	Ki	F

 

В левой части двоичный эквивалент конституент,а в правой присутствует ли она в функциональном представлении или нет.

Кроме интервалов,представленные конституентами выделим другие интервалы более крупные.

 

 

001 0х1

011 х11

100 1х0 - максимальные интервалы относительно конституент.

110 11х

 

Лемма.

Если в представление функции включен не максимальный интервал, то этот интервал может быть преобразован с помощью вычеркивания первичных термов.

Доказательство:

Исходя из определения, в функциональном представлении присутствует интервал, содержащий не максимум,а состоящий из некоторых первичных термов не максимальный интервал. Следовательно, максимальный интервал мажет быть получен вычеркиванием незначительных термов из немаксимального интервала.

М = А + В = А + В

В – максимальный интервал

В Ì В - не максимальный интервал

Вычеркиванием терма – получим максимальный интервал.

Тупиковой формой –называется нормальная форма Кантора, из которой не может быть вычеркнут ни один терм без изменения представления функции.

Минимальной формой – называется тупиковаяформа, минимальной сложности

Выражения для максимальных интервалов называются простыми импликантами.

ТЕОРЕМА.

Все тупиковые,а следовательно и минимальные формы содержатся в объединении всех простых импликант.

Доказательство:

Из определения следует,что если вНФК присутствует неминимальный интервал,то она не является тупиковой и не является минимальной.

Следовательно, тупиковой и минимальной формой есть объединение некоторых простых импликант из множества всех простых импликант.

Согласно вышеуказанной теореме 1-й шаг метода Квайна состоит в выделении простых импликант функции и составлении таблицы.

Строки соответствуют простым импликантам.

Столбцы – конституентам функции.

 

0х1
х11
1х0
11х

Если конституента содержится соответственном максимальном интервале, то в клетке ставится 1, если нет, то клетка остаётся пустой.

2-й шаг

Состоит в том, что из множества простых импликант составляются всевозможные подмножества, обладающие свойствами:

1. Элементы подмножества суммарно покрывают все конституенты функции.

2. При вычеркивании любого элемента подмножества свойство 1 не выполняется.

Подмножество, удовлетворяющее свойствам называется минимальными покрытиями таблицы Квайна.

 

ТЕОРЕМА

Возможные минимальные покрытия таблицы Квайна представляют все тупиковые формы функционального представления, среди которых содержатся и минимальные формы.

Доказательство:

Необходимость следует из того, что тупиковые и минимальные формы есть объединение простых импликант. Достаточность следует из того, что не возможно вычеркнуть простую импликанту, а следовательно любой первичный термин, без нарушения покрытия всех конституент функции.