Пример: из 2-й в 8-ю
110 100 101 =64510
6 4 5
ШЕСТНАДЦАТЕРИЧНАЯ СИСТЕМА.
Применяется для облегчения чтения записи двоичных кодов. Т.К. основанием является 16, что составляет 24, то для перевода из двоичной в шестнадцатеричную двоичное число разбивается на 4-х битовые группы, называемые тетрадами.
| b=10 | ||||||||||||||||
| b=16 | a | b | c | d | e | f |
Пример:
1011 1110 1111 1001 1101 1000 = bef9d8
b e f 9 d 8
ПОРЯДОК ПЕРЕВОДА ИЗ ОДНОЙ СИСТЕМЫ
СЧИСЛЕНИЯ В ДРУГУЮ (АЛГОРИТМ ПЕРЕВОДА). ПЕРЕВОД ЦЕЛЫХ ЧИСЕЛ.
1. Поделить данное число на основание новой системы.
2. Перевести остаток от деления в новую систему исчисления.
Получится младший разряд нового числа.
3. Если частное от деления больше основания системы, то продолжить
деление, второй остаток от деления даст 2-й разряд и т.д.
Перевести 256 из 10-й в 8-ую.
 256 8
256 8



 24 32 8
24 32 8

 16 32 4 25610=4008
16 32 4 25610=4008
16 0 4008=4*82=25610
 0
0
Перевести 397 из 10-й в 16-ую.
 397 16
397 16



 32 24 16
32 24 16
77 16 1 39710=18D16
64  8
8
 13
13
18*d=1*162+8*161+13*160=256+128+13=39710
Перевод дробной части
1.Умножить дробную часть на основание новой системы исчисления.
2.В полученном произведении выделить целую часть числа. Это будет старший разряд искомого числа.
3.Дробную часть произведения снова умножить на основание системы.
Целая часть будет следующим разрядом.
4.Выполнять умножение до получения необходимого количества разрядов.
Пример:
0,78410 перевести в двоичную
0,784
 2 0,78410=0,110012
2 0,78410=0,110012
1,568
 2
2
1,136
 2
2
0,272
 2
2
0,544
 2
2
1,088
Перевести:
0,6125 в 8-ую
0,6125
8 0,612510=0,471468
 4,9000
4,9000
 8
8
7,2000
 1,6000
1,6000
 4,8000
4,8000
Перевести: 0,378 в 16-ую
0,378
 16 0,37810=0,60c416
16 0,37810=0,60c416
2,268
 6,048
6,048
 288
288
 0,768
0,768
 12,288
12,288
 16
16
4,608
Для перевода из одной системы в другую смешанного числа, необходимо отдельно перевести целую и дробную части.
ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА
Образуется заменой каждого десятичного разряда 4-х битовым представлением.
Пример:
7 4 3 5 (743510)
0111 0100 0011 010110-2
Пример: перевести 01100101 в двоичный эквивалент.
Представим данное число через веса его разрядов:
0110*101 + 0101*100=0110(8+2)+0101
Для упрощения умножения выразим весовой коэффициент 10 в виде (8+2). Учитывая, что умножение на 8 есть сдвиг на 3 разряда влево, а
на 2 - на 2 разряда влево, то получим.
 1000001
1000001
1=1
2=21
8=23
АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ С ДВОИЧНЫМИ ЧИСЛАМИ (СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ, ДЕЛЕНИЕ)
Правило выполнения арифметических операций над двоичными числами задается соответствующими таблицами двоичного сложения, вычитания и умножения.
ТАБЛИЦА 2-ГО СЛОЖЕНИЯ.
0+0=0
0+1=1
1+0=1
1+1=0+1
ТАБЛИЦА 2-ГО ВЫЧИТАНИЯ.
0-0=0
1-0=1
1-1=0
0-1=1 с учетом из старшего разряда взяли единицу
ТАБЛИЦА 2-ГО УМНОЖЕНИЯ.
0*0=0
0*1=0
1*0=0
1*1=1
Двоичное сложение выполняется по тем же правилам, что и десятичное, за исключением того, что перенос в следующий разряд производится, как сумма достигнет 2-х.(1+1)
Пример:
11,25 1011,01
13,50 1101,10

 24,7510 11000,112
24,7510 11000,112
При вычитании 2-х чисел в данном разряде при необходимости
(когда цифра в разряде вычитаемого больше в том же разряде цифры уменьшаемого) занимается единица из следующего старшего разряда.
Эта занимаемая единица равна 2-м единицам данного разряда.
Пример:
13,50 1101,10
11,25 1011,01


 2,2510 0010,01
2,2510 0010,01
Умножение 2-х много разрядных чисел выполняется образованием частичных произведений и их последующим суммированием.
Согласно таблице двоичного умножения каждое частичное произведение равно нулю, если в соответствующем разряде множителя стоит ноль или равно множимому, сдвинутому на определенное число разрядов влево, если в разряде множителя записана еденица. Таким образом, операция умножения могоразрядных 2-х чисел сводится к операции сдвига и сложения. Положение запятой определяется также, как и при умножении десятичных чисел.
Пример:
11,5 10111

 5,25 10101
5,25 10101
60,37510 10111
 10111
10111
1111000112
Деление:
Производится аналогично десятичному делению.
Пример:


 12,375 2,25 1100,011 10,010
12,375 2,25 1100,011 10,010

 5,5 10010 101,1
5,5 10010 101,1
 10010
10010
 10010
10010
Двоичное дополнение числа.
Мы рассмотрим примеры арифметических операций, в которых используются прямые ходы. В персональных компьютерах при выполнении операции вычитания и сложения отрицательных чисел используются не прямые, а дополнительные коды, что позволяет заменить операцией сложения.
Чтобы получить дополнительный ход необходимо:
1) получить обратный код, который образуется инвертированием каждого разряда двоичного число.
прямой код: 010 110 101 011 обратный код: 101 001 010 100
2) образовать дополнительный код, который равен сумме обратного кода и еденице младшего разряда.
101 001 010 101
Пример вычитания чисел с помощью дополнительного кода.
7-3=4
0111 0111


 0011 1101
0011 1101
Единица переноса из старшего разряда отбрасывается.
Поскольку число 9 можно представить только в четырех битовым
двоичным числом, поэтому в операциях с дополнительным ходом числа всегда дополняются до четырех битового числа.
Над двоично-десятичными кодами также можно выполнять арифметические операции. При этом в результате выполнения арифметических операций получают значения запрещенных кодов, то используется прибавление или вычитание корректирующего кода.
Причем прибавление, если мы складывали, вычитание, если отнимали. Значение корректирующего кода в двоичной системе равно 0110.
ТАБЛИЦА ЗАПРЕЩЕННЫХ КОДОВ.
 2 10
2 10
1010 10
1011 11
1100 12
1101 13
1110 14
1111 15
Коды являются запрещенными, потому что в десятичной системе эти числа дают перенос в старший разряд, а двоично-десятичная система использует по четыре бита на каждый десятичный разряд, поэтому эти комбинации оказываются лишними и не используются.
Пример на сложение и вычитание
5+3=810 7+5=12
1001 0111
0011 0101

 1000 1100 – запр.
1000 1100 – запр.
0110 – коррект.код
 000100102
000100102
17+5=22 15-7=8
0001 0111 1111 0001 0101
 0101 0111 0111
0101 0111 0111

 0001 1100 10002 = 810 0000 1110
0001 1100 10002 = 810 0000 1110
 0110 0110
0110 0110
 0010 00102 0000 100010-2 = 8
0010 00102 0000 100010-2 = 8
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ.
Теория множеств является логической основой современного математического аппарата.
Основатель теории множеств Г.Кантор определял множество следующим понятием: «под множеством понимают всякую совокупность определенных элементов, которое может быть связано с помощью некоторого закона." Множество обозначают большими буквами латинского алфавита.
Объекты, составляющие множество называются его элементами и обозначаются маленькими латинскими буквами.
Для того чтобы указать, что множество состоит из элементов X применяют, вот такую форму записи:
A={X}
Если нужно указать характеристическое свойство согласно которого
объекты объединяются во множества применяется следующая запись: A={X:...} где... характеристическое свойство.
Например:
B={X:x2-1=0}
Элементами множества B является множество корней уравнения x2-1=0 КЛАССИФИКАЦИЯ МНОЖЕСТВ:
Условимся различать конечные и бесконечные множества.
Конечным множеством назовем множество, количество элементов которого
может быть выражено конечным числом, причем неважно, что это за число. Главное, что оно существует. Примерами конечных множеств может служить количество рук человека, количество букв на странице конспекта,
число букв во всех изданных книгах.
К конечным множествам мы также будем относить и пустое множество, не содержащее элементов.
К бесконечным множествам отнесем все множества, не являющиеся конечными. Примерами бесконечных множеств может служить множество
всех целых чисел, множество точек на плоскости.
Конечные множества могут быть заданы простым перечислением его
элементов.
Бесконечное множество может быть задано только указанием характеристического свойства элементов.
Пример: C={X1,X2,X3,X4}
Введем некоторые основные понятия и обозначения.
Для того чтобы указать, что X есть элемент множества A пишут: X  A
A
Чтобы указать, что X не принадлежит множеству A записывают таким образом: X  A
A
Если множества A и B совпадают, то пишут: A=B
Это означает, что элементы этих множеств одни и те же.
Пример:
B-множество всех студентов в аудитории.
A-множество всех студентов мужского пола (горный факультет).
Если элементы множества A содержатся во множестве B, то записывается это следующим образом:
A  B
B
и читается:"A содержится в B".
АКСИОМЫ ТЕОРИИ МНОЖЕСТВ
Существует 6 изначальных аксиом теории множеств:
1-Аксиома существования:
"существует хотя бы одно множество".
Все аксиомы мы будем сопровождать диаграммами Эйлера.
 |
2-Аксиома эквивалентности:
"если множество A и B состоят из одних и тех же элементов,
то они равны"
A=B
3-Аксиома объединения:
"Для двух произвольных множеств A и B существует такое множество
C, элементами которого является каждый элемент содержащийся хотя бы в одном из этих множеств".
 |
Аксиома обобщается на случай нескольких исходных множеств и звучит так:
"Для произвольных множеств Ai существует множество C, элементами которого является каждый элемент, содержащийся хотя бы в одном из этих множеств Ai".
Аналитическое выражение для двух множеств:
C =AÈB
Для операции объединения справедливы свойства:
1) AÈA=A
2) AÈI = I
3) A È Æ =A
Исходя из этих свойств бинарную операцию объединения обозначают следующим образом:
C=A+B
А множественную операцию обозначают:
M =  Mi
Mi
4-Аксиома пересечения:
"Для двух произвольных множеств A и B существует множество C элементами которого является каждый элемент, принадлежащий как множеству A, так и множеству B".
 |
Аналитически записывается C=A Ç B
читается множество C равно пересечению множеств A и B.
Для операции пересечения справедливы следующие соотношения:
1) A Ç A = A
2) A Ç I = I
3) A Ç Æ =Æ
Обобщенная аксиома на случай нескольких исходных множеств:
"Для произвольных множеств Ai существует множество C, элементами которого является каждый элемент, принадлежащий множествам Ai одновременно".
Далее бинарная операция будет обозначаться:
C=A*B
А множественная:
M=  Mi
Mi
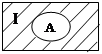
5-Аксиома универсального множества:
"Для произвольной группы множеств Ai всегда можно выбрать такое множество I, что Ai Ì I".
Множество I назовем единичным множеством универсальным.
6-Аксиома пустого множества:
"Всегда существует пустое множество - Æ, которому не принадлежит ни один элемент, иначе нулевое множество".
ДОПОЛНИТЕЛЬНЫЕ ОПЕРАЦИИ НАД МНОЖЕСТВАМИ.
1.Операция отрицания:
"Для произвольного множества A существует дополнение к единичному множеству, обозначаемое  (не A)".
(не A)".
Следствие:
1) A È  = I
= I
2) A Ç  = Æ
= Æ
Графически изображается следующим образом:
 |
2.Разность между множествами:
"Для произвольных множеств A,B существует множество C, определяемое как
1. C=A\B=A Ç 
2. C=B\A=B Ç 
Первая формула читается A без B, вторая - B без A.
Графически выглядит следующим образом:
 |
Бинарная операция выглядит следующим образом C=A-B
3.Симметрическая разность множеств A,B.
C=A \ B È B \ A
Графически выглядит следующим образом:

Бинарная операция может быть записана следующим образом:
C=(A-B)+(B-A)=A 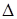 B
B
ЗАКОНЫ ДЛЯ ПЕРЕСЕЧЕНИЯ И ОБЪЕДИНЕНИЯ.
Исходя из формулировки объединения и пересечения:
1. Закон коммутативности
A È B = B È A
A Ç B = B Ç A
2. Закон ассоциативности
AÈ(BÈC)=(AÈB)ÈC
AÇ(BÇC)=(AÇB)ÇC
3. Закон дистрибутивности
- (AÈB)ÇC=(AÇC)È(BÇC)
Доказательство:
Рассмотрим выражение в левой части:
М=(AÈB)ÇC
Если х 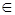 М, то значит, что х
М, то значит, что х 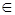 С и одновременно
С и одновременно 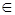 А или
А или 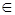 В
В
 Когда х
Когда х 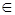 А, х
А, х 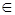 (АÇС), а когда х
(АÇС), а когда х 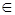 В х
В х 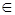 (ВÇС)
(ВÇС)
Объединение этих выражений даёт правую часть.
- (АÇВ)ÈС=(АÈС)Ç(ВÈС)
Доказательство:
Возьмем правую часть равенства. Согласно закону ассоциативности
раскроем скобки и получим:
(АÈС)Ç(ВÈС)=АÇВÈСÇВÈАÇСÈСÇС=АÇВÈС (упростили используя
закон поглощения). Из записи закона ассоциативности и закона
дистрибутивности видно, что один закон можно получить из другого,
заменив знаки “È” и “Ç”, следовательно, законы двойственны.
4. Закон поглощения
Если А содержится в В, то АÈB=В.
Согласно аксиоме объединения в результирующее множество входят элементы, принадлежащие хотябы одному А или В, а так как все А входят в В то справедливо:
АÈB=В
АÈАÇМ=А
Исходя из определения операции пересечения ясно, что АÇМ содержится в А.В итоге получаем А.
Следствие:
Если М=1, то АÈА=А
5. Свойство степени.
Если множество пересекается с самим собой, то из определения пересечения следует
АÇА=А
Законы де Моргана.
Эти законы позволяют выразить законы объединения и пересечения друг через друга с использованием операции дополнения:
 а) АÈВ=
а) АÈВ=  Ç
Ç 

Доказательство:
Обозначим через М: М=АÈВ и  =
=  Ç
Ç  . Если теперь объединение М и
. Если теперь объединение М и  даст единичное множество, то закон будет доказан.
даст единичное множество, то закон будет доказан.
М È  = А È В È
= А È В È  Ç
Ç  = АÈ(В È
= АÈ(В È  )Ç(В È
)Ç(В È  ). Используя определение дополнения получим:
). Используя определение дополнения получим:
М È  = АÈВÈ
= АÈВÈ  =1ÈВ=1=I
=1ÈВ=1=I
 б) АÇВ=
б) АÇВ=  È
È 

Доказательство:
Обозначим через М: М=АÇВ и  =
=  È
È  . Если теперь объединение М и
. Если теперь объединение М и  даст единичное множество, то закон будет доказан.
даст единичное множество, то закон будет доказан.
М È  = А Ç В È
= А Ç В È  Ç
Ç  =(
=( È А) Ç (В È
È А) Ç (В È  )È
)È  = ВÈ
= ВÈ  È
È  =1È
=1È  =1=I
=1=I
Законы де Моргана так же являются двойственными.
АÇВ=АВ.
ВЫВОДЫ ПО РАЗДЕЛУ.
1. АÌА
2. Если АÌВ и ВÌА, то А=В
3. Если АÌВ и ВÌС, то АÌС
4. Æ Ì A
5. А Ì I
6. А È В =В È А
7. А Ç В =В Ç А
8. АÈ(ВÈС)=(АÈВ)ÈС
9. АÇ(ВÇС)=(АÇВ)ÇС
10. А È А = А
11. А Ç(ВÈС)=(АÇВ)È(АÇС)
12. А È (ВÇС)=(АÈВ) Ç (АÈС)
13. А È Æ = А
14. А È I= I
15. А Ç I = A
16. А Ç A = A
17. А Ç Æ = Æ
18. Если АÌВ, то АÈВ=В, АÇВ=А
19. А È  = I
= I
20. A Ç  = Æ
= Æ
21.  =I
=I
22.  =Æ
=Æ
23.  = A
= A
24. Если АÌВ, то  Ì
Ì 
25. ( ) =
) =  Ç
Ç 
26. ( ) =
) =  È
È 






