ѕерва€ и основна€ задача кинематики - определение функции положени€. ƒл€ пространственных механизмов наиболее эффективными методами решени€ этой задачи €вл€ютс€ векторный метод и метод преобразовани€ координат. ѕри решении пр€мой задачи о положении схвата манипул€тора обычно используют метод преобразовани€ координат. »з множества методов преобразовани€ координат [ 1, 2 ], которые отличаютс€ друг от друга правилами выбора осей локальных систем координат, дл€ манипул€торов обычно используетс€ метод ƒенавита и ’артенберга.
ќпишем два вида матриц:
матрицы ћ, определ€ющие отношение между системами координат соседних звеньев;
матрицы “, определ€ющие положение и ориентацию каждого звена механизма в неподвижной или базовой системе координат.
¬оспользуемс€ однородными координатами трехмерного проективного пространства –R3, в которых движение евклидова пространства R3 можно представить линейным преобразованием
 где ћij - матрица 4x4 вида
где ћij - матрица 4x4 вида  .
.
Ёто преобразование эквивалентно преобразованию в эвклидовом пространстве  где
где  . “о есть преобразованию, которое включает поворот, определ€емый матрицей Uij размерностью 3х3, и параллельный перенос, задаваемый вектором
. “о есть преобразованию, которое включает поворот, определ€емый матрицей Uij размерностью 3х3, и параллельный перенос, задаваемый вектором  размерностью 3. ¬ однородном пространстве положение точки будут определ€ть не три x, y и z, а четыре величины x', y', z' и t', которые удовлетвор€ют следующим соотношени€м:
размерностью 3. ¬ однородном пространстве положение точки будут определ€ть не три x, y и z, а четыре величины x', y', z' и t', которые удовлетвор€ют следующим соотношени€м:
x = x'/t', y = y'/t', z = z'/t'.
ќбычно принимают t'=1. ” матрицы поворота Uij элементами uij €вл€ютс€ направл€ющие косинусы углов между новой осью i и старой осью j. ¬ектор  - трехмерный вектор, определ€ющий положение начала новой системы координат i в старой системе j. ¬ыбор расположени€ осей должен соответствовать решаемой задаче. ѕри решении задачи о положени€х необходимо: в пр€мой задаче определить положение выходного звена как функцию перемещений в приводах, в обратной - заданное положение выходного звена представить как функцию перемещений в приводах. ¬ыбор расположени€ и ориентации локальных систем координат должен обеспечивать выполнение этих задач. ѕри использовании метода ƒенавита и ’артенберга оси координат располагаютс€ по следующим правилам:
- трехмерный вектор, определ€ющий положение начала новой системы координат i в старой системе j. ¬ыбор расположени€ осей должен соответствовать решаемой задаче. ѕри решении задачи о положени€х необходимо: в пр€мой задаче определить положение выходного звена как функцию перемещений в приводах, в обратной - заданное положение выходного звена представить как функцию перемещений в приводах. ¬ыбор расположени€ и ориентации локальных систем координат должен обеспечивать выполнение этих задач. ѕри использовании метода ƒенавита и ’артенберга оси координат располагаютс€ по следующим правилам:
1. ƒл€ звена i ось zi направл€етс€ по оси кинематической пары, образуемой им со звеном (i+1). Ќачало координат размещают в геометрическом центре этой пары.
2. ќсь xi направл€етс€ по общему перпендикул€ру к ос€м zi-1 и zi с направлением от zi-1 к zi. ≈сли оси zi-1 и zi совпадают, то xi перпендикул€рна к ним и направлена произвольно. ≈сли они пересекаютс€ в центре кинематической пары, то начало координат располагаетс€ в точке пересечени€, а ось xi направл€етс€ по правилу векторного произведени€  (кратчайший поворот оси zi до совмещени€ с zi-1 при наблюдении с конца xi должен происходить против часовой стрелки).
(кратчайший поворот оси zi до совмещени€ с zi-1 при наблюдении с конца xi должен происходить против часовой стрелки).
3. ќсь yi направл€етс€ так, чтобы система координат была правой.
¬ пр€мой задаче необходимо определить положение схвата манипул€тора и св€занной с ним системы координат Mxnynzn по отношению к неподвижной или базовой системе координат Kx0y0z0. Ёто осуществл€етс€ последовательными переходами из системы координат звена i в систему координат звена i-1. —огласно прин€тому методу, каждый переход включает в себ€ последовательность четырех движений: двух поворотов и двух параллельных переносов, осуществл€емых в указанной последовательности (см. рис. 20.1):
|
|
|
- поворот i -ой системы вокруг оси xi на угол -qi до параллельности осей zi и zi-1 (положительное направление поворота при наблюдении с конца вектора xi против часовой стрелки);
- перенос вдоль оси xi на величину -ai до совмещени€ начала системы координат Oi с точкой пересечени€ осей xi и zi-1 (отсчет по оси xi от точки пересечени€ оси xi и оси zi-1);

|
| –ис. 20.1 |
- перенос вдоль оси zi-1 на величину -si, после которого начало системы координат Oi оказываетс€ в начале координат Oi-1 системы (i-1) (отсчитываетс€ по оси zi-1 от ее начала координат Oi-1 до точки ее пересечени€ с осью xi);
- поворот вокруг оси zi-1 на угол -ji, до тех пор пока ось xi не станет параллельной оси xi-1 (положительное направление поворота при наблюдении с конца вектора zi-1 против часовой стрелки).
Ќеобходимо отметить, что знак угла поворота не имеет значени€, так как в матрицах перехода используютс€ направл€ющие косинусы (четные функции). ÷елесообразно рассматривать угол, обеспечивающий кратчайший поворот оси старой системы i до совмещени€ (параллельности) с соответствующей осью новой (i-1). ѕеремещени€ начала координат определ€ютс€ как координаты начала старой системы Oi в новой Oi-1.
¬ манипул€торах обычно используютс€ одноподвижные кинематические пары или вращательные, или поступательные. ќба относительных движени€ как вращательное, так и поступательное, реализуютс€ в цилиндрических парах. ѕоэтому при общем представлении механизма используютс€ (рис.20.1) цилиндрические пары.
ћатрицы перехода их системы Oi в систему Oi-1 можно записать так:
 ,
,
| где: | 
| - матрица поворота вокруг оси xi на угол -qi, |

| - матрица переноса вдоль оси xi на -ai, | |

| - матрица переноса вдоль оси zi-1 на -si, | |

| - матрица поворота вокруг оси zi-1 на угол -ji. |
¬ этих матрицах переменные si и j i соответствуют относительным перемещени€м звеньев в кинематических парах и €вл€ютс€ обобщенными координатами манипул€тора, определ€ющими конфигурацию механизма в рассматриваемом положении. ѕеременные ai и q i определ€ютс€ конструктивным исполнением звеньев манипул€тора, в процессе движени€ они остаютс€ неизменными.
ѕоложение некоторой произвольной точки ћ в системе координат звена i определ€етс€ вектором rMi, а в системе координат звена (i-1) - вектором rMi-1. Ёти радиусы св€заны между собой через матрицу преобразовани€ координат ћi следующим уравнением:
 ,
,
| где: | 
| - матрица перехода из i -ой системы координат в (i - 1) -ю. |
–ассмотрим шестиподвижный манипул€тор в исходном или начальном положении (рис.20.2). «а начальное положение принимаетс€ такое, в котором все относительные обобщенные координаты равны нулю. ѕереход из системы координат любого i -го звена к неподвижной или базовой системе записываетс€ в виде
 или
или  ,
,
где  - матрица преобразовани€ координат i -ой системы в координаты базовой системы координат.
- матрица преобразовани€ координат i -ой системы в координаты базовой системы координат.

|
| –ис. 20.2 |
ƒл€ схемы, изображенной на рис.20.2, радиус rM6 = 0, а радиус rM0 определитс€ по формуле
 ,
,
то есть положение выходного звена манипул€тора определ€етс€ матрицей “n. Ёлементы этой матрицы определ€ют положение центра схвата точки ћ и ориентацию его в пространстве. „етвертый столбец определ€ет, декартовы координаты точки ћ (проекции вектора rM0 на оси координат). “ретий столбец содержит направл€ющие косинусы оси zn системы координат, св€занной со схватом, или вектора подхода  , который характеризует направление губок схвата (рис.20.3). ¬торой столбец определ€ет направление оси yn или вектора ориентации
, который характеризует направление губок схвата (рис.20.3). ¬торой столбец определ€ет направление оси yn или вектора ориентации  , который проходит через центр схвата по оси перпендикул€рной рабочим поверхност€м его губок. ¬ первом столбце содержатс€ направл€ющие косинусы оси xn или вектора
, который проходит через центр схвата по оси перпендикул€рной рабочим поверхност€м его губок. ¬ первом столбце содержатс€ направл€ющие косинусы оси xn или вектора 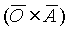 . ”глом подхода схвата
. ”глом подхода схвата  называетс€ угол между вектором подхода
называетс€ угол между вектором подхода  и базовым вектором
и базовым вектором
|
|
|
 ,
,
где  - орт вектора
- орт вектора  неподвижной или базовой системы координат. — учетом сказанного, матрица Tn может быть представлена в следующем виде
неподвижной или базовой системы координат. — учетом сказанного, матрица Tn может быть представлена в следующем виде
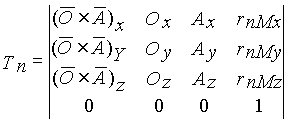

|
| –ис. 20.3 |
¬ результате матричных преобразований получаем радиус-вектор точки ћ схвата в функции обобщенных координат. ќбычно, за обобщенные координаты принимают линейные и угловые перемещени€ в кинематических парах или на выходных валах приводов манипул€тора. ¬ механизме с n подвижност€ми в общем виде функцию положени€ схвата можно записать так

где q1, q2,... qn - обобщенные координаты манипул€тора.
ѕри кинематическом анализе манипул€тора в пр€мой задаче необходимо определить линейные и угловые скорости и ускорени€ схвата при заданных угловых и линейных обобщенных скорост€х и ускорени€х (обычно относительных скорост€х и ускорени€х в кинематических парах механизма). ¬ обратной задаче по заданному закону изменени€ скоростей и ускорений схвата определ€ютс€ законы изменени€ скоростей и ускорений в ѕ или на выходных звень€х приводов. –ешение пр€мой задачи кинематики дл€ точки ћ схвата можно получить продифференцировав четвертый столбец матрицы “n по времени

|
”гловую скорость и угловое ускорение схвата можно определить векторным суммированием относительных угловых скоростей во вращательных ѕ механизма. “ак как вектора угловых скоростей, при данном выборе ориентации осей координат, совпадают с осью z, то углова€ скорость схвата

где  орт оси z системы координат, расположенной в центре ѕ, соедин€ющей звено i и звено i-1, m - число вращательных ѕ в механизме.
орт оси z системы координат, расположенной в центре ѕ, соедин€ющей звено i и звено i-1, m - число вращательных ѕ в механизме.
ƒифференциру€ это выражение по времени, получим формулу дл€ определени€ углового ускорени€ схвата:







