1. Определение закона движения. Если в задании на проектирование не дан закон движения, то конструктор должен выбрать его и набора типовых
Таблица 17.1
| №п.п. | Типовой закон движения | Параметры закона движения | ||||
| 1. | 
| с жесткими ударами
| ||||
| 2. | 
| с мягкими ударами aq1¹aq2; jур¹jур; aq1×jур = aq2×jут или aq1 = aq2; jур = jур; aq1×jур = aq2×jут | ||||
| 3. | 
| с мягкими ударами aq1 ¹ aq2; jур ¹ jут; aq3 ¹ aq4 ; (aq1+aq2)× jур = =(aq3+aq4)×jут | ||||
| 4. | 
| с мягкими ударами aq1 ¹ aq2; jур¹jут; 0.5× aq1×jур= 0.5× aq2×jут | ||||
| 5. | 
| безударный aq1 ¹ aq2; jур¹jут; 0.5× aq1×jур= 0.5× aq2×jут | ||||
| 6. | 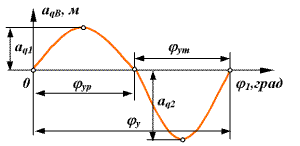
| безударный aq1 ¹ aq2; jур¹jут ;

|
законов движения (табл.17.1). Типовые законы движения делятся на законы с жесткими и мягкими ударами и законы безударные. С точки зрения динамических нагрузок, желательны безударные законы. Однако кулачки с такими законами движения технологически более сложны, так как требуют более точного и сложного оборудования, поэтому их изготовление существенно дороже. Законы с жесткими ударами имеют весьма ограниченное применение и используются в неответственных механизмах при низких скоростях движения и невысокой долговечности. Кулачки с безударными законами целесообразно применять в механизмах высокими скоростями движения при жестких требованиях к точности и долговечности. Наибольшее распространение получили законы движения с мягкими ударами, с помощью которых можно обеспечить рациональное сочетание стоимости изготовления и эксплуатационных характеристик механизма.
После выбора вида закона движения, обычно методом кинематических диаграмм, проводят геометро-кинематическое исследование механизма и определяют закон перемещения толкателя и закон изменения за цикл первой передаточной функции (см. лекцию 3 - метод кинематических диаграмм).
2. Определение основных размеров кулачкового механизма. Размеры кулачкового механизма определяются с учетом допустимого угла давления в высшей паре. При этом используется условие, доказанное выше, и названное нами вторым следствием основной теоремы зацепления.
Формулировка синтеза: Если на продолжении луча, проведенного из точки О2 через точку K, отложить от точки K отрезок длиной lKD = VK2 / w1 = VqK2 и через конец этого отрезка провести прямую параллельную контактной нормали, то эта прямая пройдет через центр вращения ведущего звена точку О1 .
Условие, которому должно удовлетворять положение центра вращения кулачка О 1, согласно этой теореме: углы давления на фазе удаления во всех точках профиля должны быть меньше допустимого значения. Поэтому графически область расположения точки О 1 может быть определена семейством прямых проведенных под допустимым углом давления к вектору возможной скорости точки центрового профиля, принадлежащей толкателю. Графическая интерпретация вышесказанного для толкателя и коромысла дана на рис. 17.5. На фазе удаления строится диаграмма зависимости S B = f(j1). Так как при коромысле точка В движется по дуге окружности радиуса lBC , то для механизма с коромыслом диаграмма строится в криволинейных координатах. Все построения на схеме, проводятся в одном масштабе, то есть ml= mVq= mS.

Рис.17.5
| Механизм с толкателем | Механизм с коромыслом |
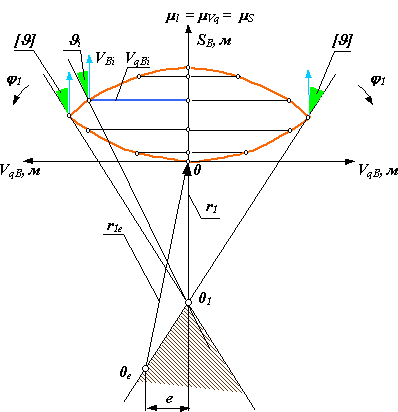
Выбор центра возможен в заштрихованных областях. Причем выбирать нужно так, чтобы обеспечить минимальные размеры механизма. Минимальный радиус r1* получим, если соединим вершину полученной области, точку О1*, с нача-лом координат. При таком выборе радиуса в любой точке профиля на фазе удаления угол давления будет меньше или равен допустимому. Однако кулачок необходимо при этом выполнить с эксцентриситетом е*. При нулевом эксцентри-ситете радиус начальной шайбы определится точкой Ое0. Величина радиуса при этом равна re0, то есть значительно больше минимального. При выходном звене - коромысле, минимальный радиус определяется аналогично. Радиус начальной шайбы кулачка r1aw при заданном межосевом расстоянии aw, определяется точкой О1aw, пересечения дуги радиуса aw с соответствующей границей области. Обычно кулачок вращается только в одном направлении, но при проведении ремонтных работ желательно иметь возможность вращения кулачка в противо-положном направлении, то есть обеспечить возможность реверсивного движения кулачкового вала. При изменении направления движения, фазы удаления и сближения, меняются местами. Поэтому для выбора радиуса кулачка, движуще-гося реверсивно, необходимо учитывать две возможных фазы удаления, то есть строить две диаграммы S В= f (j1) для каждого из возможных направлений дви-жения. Выбор радиуса и связанных с ним размеров реверсивного кулачкового механизма проиллюстрирован схемами на рис. 17.6.
На этом рисунке:
r1 - минимальный радиус начальной шайбы кулачка;
r1е - радиус начальной шайбы при заданном эксцентриситете;
r1aw - радиус начальной шайбы при заданном межосевом расстоянии;
aw0 - межосевое расстояние при минимальном радиусе.
 Механизм с толкателем
Механизм с толкателем
|
 Механизм с коромыслом
Рис.17.6
Механизм с коромыслом
Рис.17.6
|
Примечание: В некоторых методических указаниях диаграмма SВ= f( j1) называется фазовым портретом, а плоскость на которой она построена называется фазовой плоскостью. Правомерность применения этих терминов в данном случае сомнительна. Фазовая плоскость и фазовый портрет используются в теории колебаний для изучения процессов зависящих от времени (т.е. динамических процессов). При метрическом синтезе кулачка решается чисто геометрическая задача параметры в которой не зависят от времени. Поэтому рекомендуется воздерживаться от применения вышеуказанных терминов.
Выбор радиуса ролика (скругления рабочего участка толкателя).
При выборе радиуса ролика руководствуются следующими соображениями:
- Ролик является простой деталью, процесс обработки которой несложен (вытачивается, затем термообрабатывается и шлифуется). Поэтому на его поверхности можно обеспечить высокую контактную прочность. В кулачке, из-за сложной конфигурации рабочей поверхности, это обеспечить сложнее. Поэтому обычно радиус ролика rр меньше радиуса начальной шайбы конструктивного профиля r и удовлетворяет соотношению rр < 0.4× r0
,где r0 - радиус начальной шайбы теоретического профиля кулачка. Выполнение этого соотношения обеспечивает примерно равную контактную прочность как для кулачка, так и для ролика. Ролик обладает большей контактной прочностью, но так как его радиус меньше, то он вращается с большей скоростью и рабочие точки его поверхности участвуют в большем числе контактов. - Конструктивный профиль кулачка не должен быть заостренным или срезанным. Поэтому на выбор радиуса ролика накладывается ограничение
rр <0.7 ×rmin , где rmin - минимальный радиус кривизны теоретического профиля кулачка (см. рис. 17.7).

Рис.17.7
- Рекомендуется выбирать радиус ролика из стандартного ряда диаметров в диапазоне rp = (0.2... 0.35) × r0 . При этом необходимо учитывать, что увеличение радиуса ролика увеличивает габариты и массу толкателя, ухудшает динамические характеристики механизма (уменьшает его собственную частоту). Уменьшение радиуса ролика увеличивает габариты кулачка и его массу; частота вращения ролика увеличивается, его долговечность снижается.
- При выборе радиуса скругления рабочего участка толкателя подход к решению задачи несколько иной. Так как в этом случае нет местной подвижности, заменяющей скольжение качением, то на толкателе имеется очень небольшой рабочий участок, точки которого скользят относительно рабочей поверхности кулачка, то есть износ поверхности толкателя более интенсивный. Увеличение радиуса скругления не увеличивает габаритов и массы толкателя, а размеры конструктивного профиля кулачка уменьшаются. Поэтому этот радиус можно выбирать достаточно большим. Часто применяются толкатели с плоской рабочей поверхностью кулачка (радиус скругления равен бесконечности). В этом случае угол давления в высшей паре при поступательном движении толкателя есть величина постоянная и равная углу между нормалью к плоскости толкателя и вектором скорости его движения на фазе удаления. Определение размеров по углу давления при этом невозможно. Радиус кулачка при этом определяют по контактным напряжениям, а форму профиля проверяют по условию выпуклости (1).
3. Построение центрового и конструктивного профилей кулачка.
3.1. Для кулачкового механизма с внеосным толкателем.:
Построение профилей кулачка проводится в следующей последовательности:
- выбирается масштаб построения ml,мм/м
- из произвольного центра проводятся в масштабе окружности с радиусами r0 и е.
- из произвольной точки на окружности r0 в направлении - j1 откладываeтся рабочий угол, угол делятся на n интервалов.
- из каждой точки деления касательно к окружности радиусом е проводятся прямые.
- на этих прямых от точки пересечения с окружностью r0 откладываются в масштабе ml соответствующие перемещения толкателя SВi.
- полученные точки соединяются плавной кривой, образуя центровой профиль кулачка.
- проводятся из произвольных точек выбранных равномерно по центровому профилю кулачка дуги окружностей радиуса rp.
- конструктивный профиль кулачка получаем как огибающую к множеству положений ролика толкателя.
3.1. Для кулачкового механизма с коромыслом:
Построение профилей кулачка проводится в следующей последовательности:
- выбирается масштаб построения ml,мм/м,
- из произвольного центра проводятся в масштабе окружности с радиусами r0 и aw,
из произвольной точки на окружности aw в направлении - j1 откладываeтся рабочий угол, угол делится на n интервалов, из каждой точки деления радиусом lBC проводятся дуги.

Рис.17.8

Рис.17.9
- на этих дугах от точки пересечения с окружностью r0 откладываются в масштабе ml соответствующие перемещения толкателя SВi.
- полученные точки соединяются плавной кривой, образуя центровой профиль кулачка.
- проводятся из произвольных точек выбранных равномерно по центровому профилю кулачка дуги окружностей радиуса rр.
- конструктивный профиль кулачка получаем как огибающую к множеству положений ролика толкателя.
Проверка результатов синтеза по диаграмме углов давления
1. Построение диаграммы углов давления для механизма с геометрическим замыканием высшей пары.
Как отмечено выше, ведущим звено в течение всего цикла кулачок является только в механизме с геометрическим замыканием. Причем на фазе удаления рабочим является либо второй профиль кулачка (рис.17.1), либо другой участок поверхности толкателя, либо второй ролик. Поэтому на диаграмме угла давления необходимо четко различать фазы удаления и сближения. На рис. 17.10 дан пример диаграммы угла давления для механизма с коромыслом при геометрическом замыкании. При синтезе эта диаграмма позволяет проверить какие углы давления обеспечивают выбранные размеры механизма и полученный профиль кулачка. Угол давления определяем как острый угол между нормалью к профилю (прямая соединяющая точку контакта с центром ролика) и направлением перемещения точки В толкателя.

Рис.17.10
При построении диаграммы угла давления для механизма с силовым замыканием необходимо учитывать, что рассматриваемый при проектировании угол давления в высшей паре имеет смысл только на фазе удаления. На фазе сближения толкатель двигается под действием силы упругости пружины или сил веса. здесь угол давления - это угол между вектором этой силы и вектором скорости точки ее приложения на толкателе. Поэтому для механизмов с силовым замыканием диаграмма строится только на фазе удаления.

Рис.17.11
Для механизма с реверсивным вращением кулачка необходимо построить две диаграммы угла давления. При изменении направления движения фазы удаления и сближения меняются местами. Поэтому диаграммы угла давления строятся для фазы удаления при каждом направлении движения.
Профиль кулачка будет удовлетворять заданным условиям, если значения угла давления на фазах удаления по модулю будут меньше или равны допустимой величине угла давления.

Контрольные вопросы к лекции 17
1. Назовите особенности кулачковых механизмов, обусловившие их широкое применение в различных машинах и приборах.(стр.1-2)
2. Каковы недостатки кулачковых механизмов?(стр.2-4)
3. Изобразите схемы наиболее распространенных плоских и пространственных кулачковых механизмов.(стр.2-5)
4. Как подразделяются кулачковые механизмы по способу замыкания высшей пары? (стр.2)
5. Перечислите основные фазы движения толкателя кулачкового механизма и соответствующие им углы поворота кулачка.(стр.3)
6. Расскажите об основных этапах синтеза кулачковых механизмов.(стр.6-7)
7. Какие законы движения толкателя рационально применять в быстроходных кулачковых механизмах и почему?(стр.7-8)
8. Как определить положение центра вращения кулачка в механизме с поступательно двигающемся толкателем при заданном допустимом угле давления?(стр.8-10)
9. Как определить положение центра вращения кулачка в механизме с качающемся толкателем при заданном допустимом угле давления? (стр.8-10)
10. Из каких соображений выбирается величина радиуса ролика кулачкового механизма? (стр.11)
11. Как по теоретическому (центровому) профилю кулачка построить действительный(конструктивный) профиль? (стр.11-12)
Волновые передачи
Краткое содержание: Назначение и области применения.Преимущества и недостатки волновых передач.Классификация типовых структурных схем ВЗП.Структура волновой зубчатой передачи.Кинематика волнового механизма. Расчет геометрии волнового зубчатого зацепления.
Контрольные вопросы | Список дополнительной литературы
Назначение и области применения
Волновой передачей называется зубчатый или фрикционный механизм, предназначенный для передачи и преобразования движения (обычно вращательного), в котором движение преобразуется за счет волновой деформации венца гибкого колеса специальным звеном (узлом) - генератором волн. Основными элементами дифференциального волнового механизма являются: входной или быстроходный вал с генератором волн, гибкое колесо с муфтой, соединяющей его с первым тихоходным валом, жесткое колесо, соединенное со вторым тихоходным валом, корпус.

Рис. 18.1
Существует большое количество конструкций волновых механизмов. Обычно эти механизмы преобразуют входное вращательное движение в выходное вращательное или поступательное. Волновые механизмы можно рассматривать как одну из разновидностей многопоточных планетарных механизмов, так как они обладают многозонным, а в случае зубчатого механизма, и многопарным контактом выходного звена с гибким колесом. Многозонный контакт обеспечивается за счет формы генератора волн (кулачок чаще с двумя, редко с тремя выступами), многопарный - за счет податливости зубчатого венца гибкого колеса. Такое сочетание позволяет волновым механизмам передавать значительные нагрузки при малых габаритах. Податливость зубчатого венца обеспечивает достаточно равномерное распределение нагрузки по зубьям, находящимся в зоне зацепления. При номинальных нагрузках процент зубьев находящихся в зацеплении составляет 15-25% от общего их числа. Поэтому в волновых передачах применяется мелкомодульное зацепление, а числа зубьев колес лежат в пределах от 100 до 600. Зона зацепления в волновой зубчатой передаче совпадает с вершиной волны деформации. По числу зон или волн передачи делятся на одноволновые, двухволновые и так далее. Передачи с числом волн более трех применяются редко. Распределение передаваемых усилий по нескольким зонам уменьшает нагрузку на элементы пар и позволяет существенно уменьшать габаритные размеры и массу механизмов. Многозонный и многопарный контакт звеньев существенно увеличивает жесткость механизма, а за счет осреднения ошибок и зазоров, уменьшает мертвый ход и кинематическую погрешность механизма. Поэтому волновые механизмы обладают высокой кинематической точностью и, несмотря на наличие гибкого элемента, достаточно высокой жесткостью. Образующиеся в структуре волнового механизма внутренние контуры, увеличивают теоретическое число избыточных или пассивных связей в механизме. Однако гибкое колесо за счет податливости компенсирует ряд возникающих перекосов. Поэтому при изготовлении и сборке волновых механизмов число необходимых компенсационных развязок меньше чем в аналогичных механизмах с жесткими звеньями.
Гибкое колесо обеспечивает волновым передачам возможность передачи движения через герметичную стенку, которая разделяет две среды (например, космический аппарат и открытый космос). При этом гибкое колесо выполняется как элемент герметичной стенки, входной вал и генератор волн располагаются по одну сторону стенки (внутри космического аппарата), а выходное звено - по другую (в космическом пространстве). Схема герметичной волновой передачи приведена на рис. 18.2.

Рис. 18.2






