Соединением «треугольник» называется такое соединение, при котором конец фазы а соединяется с началом фазы b, конец фазы b - с началом фазы c и конец фазы с - с началом фазы а. К точкам соединения начал и концов фаз присоединяют линейные провода. На рис. 4.1. показана схема соединения приемников энергии «треугольником», а соединение обмоток (фаз) генератора «звездой».
Рис. 4.1. Схема соединения приемников энергии «треугольником» и обмоток генератора «звездой»
Положительные направления линейных токов IA, IB, и IC приняты от генератора к приемнику, и фазных токов Iab, Ibc и Ica от “ a ” к “ b ”, от “ b ” к “ c ” и от “ c ” к “ a ”. При соединении «треугольником», как это видно на рис. 4.1, линейное напряжение Uл равно фазному напряжению Uл = Uф. Следовательно, фазные напряжения приемника Uab, Ubc, Uca будут равны линейным напряжениям сети.
Соотношения между линейными и фазными токами найдем, применяя первый закон Кирхгофа для узлов а, b и с (рис. 4.1)
;
;
;
откуда
;
;
;
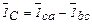т.е. линейные токи равны геометрическим разностям соответствующих фазных токов. Из этих формул видно, что геометрическая сумма линейных токов равна нулю:
;
1. Симметричная (равномерная) нагрузка фаз.
На рис.4.2, показана векторная диаграмма напряжений и токов для симметричной нагрузки фаз, т.е.
;
;
;
,
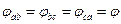Опустив перпендикуляр из конца вектора фазного тока Iab (рис.4.2.) на вектор линейного тока IA, получим прямоугольный треугольник ОЕД, из которого имеем:
,
откуда
,
т.е. линейный ток больше фазного тока 
раза. Фазный ток равен:
,
где z, R и X - полное, активное и реактивное сопротивления приемника энергии.
Коэффициент мощности приемника энергии 
.
Рис.4.2. Векторная диаграмма напряжений и токов при активно-индуктивной нагрузке фаз
На рис.4.3 показана векторная диаграмма напряжений и токов чисто активной (симметричной) равномерной нагрузки фаз.
Рис.4.3. Векторная диаграмма напряжений и токов при чисто активной симметричной нагрузке фаз
Из векторной диаграммы (рис.4.3) видно, что при неизменных линейных напряжениях фазные токи Iab, Ibc, Ica одинаковы, благодаря чему и линейные токи Ia, Ib, Ic также одинаковы.
2. Несимметричная (неравномерная) нагрузка фаз. При несимметричной нагрузке фаз токи в отдельных фазах равны:
;
;
;
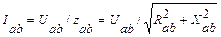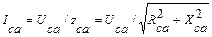где 
, 
, 
, 
, 
, 
, 
, 
, 
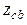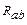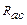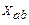- полные, активные и реактивные сопротивления фаз приемников.
Коэффициент мощности отдельных фаз приемников:
;
;
.
Для активной нагрузки:
;
;
.
Фазные токи совпадают по фазе c соответствующими напряжениями (рис.4.4)
Рис.4.4. Векторная диаграмма напряжений и токов при чисто активной несимметричной нагрузке фаз
3. Перегорание предохранителя или обрыв линейного провода.
При перегорании предохранителя в одном из линейных проводов, например, в проводе А (рис.4.5), или обрыве этого провода, лампы в фазе bc будут гореть нормально. Лампы в двух других фазах ab и ca будут соединены последовательно и находиться под линейным напряжением Uca. Если сопротивления ламп накаливания этих фаз будут одинаковы, то линейное напряжение распределится между ними поровну, т.е. лампы накаливания в этих фазах будут гореть в полнакала. В этом случае схема превращается в однофазную разветвленную цепь.
Ток в фазах ab и ca равен:
.
Ток в фазе bc равен:
.
Рис.4.5. Схема соединения приёмников электроэнергии «треугольником» при обрыве линейного провода А
Напряжение на лампах накаливания
,
,
.
Линейный ток
.
Векторная диаграмма напряжений и токов для рассматриваемого случая (рис.4.5) показана на рис.4.6.
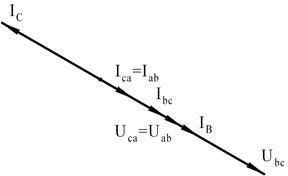
Рис.4.6. Векторная диаграмма напряжений и токов при обрыве линейного провода А
4. Обрыв фазы при несимметричной нагрузке фаз.
Если произойдет обрыв или разгрузка какой-либо фазы, например, фазы ab, то ее сопротивление будет равно бесконечности, и ток в ней будет равен нулю ( Iab= 0, рис.4.7). Фазные напряжения не изменяются.
Рис.4.7. Схема соединения приемников электроэнергии «треугольником» при обрыве фазы ab
Применим первый закон Кирхгофа к узлам а, b и с (рис.4.7). Тогда линейный ток в проводе А, будет равен току в фазе са с обратным знаком 
; линейный ток IB в проводе В равен фазному току Ibc;линейный ток в проводе С равен геометрической разности токов в фазах bc и са: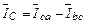 
или 
(рис.4.8).
Рис.4.8. Векторная диаграмма напряжений и токов при обрыве фазы аb
Активная мощность трехфазного тока при несимметричной (неравномерной) нагрузке фаз равна сумме активных мощностей всех фаз.
где 
, 
, 
- активные мощности отдельных фаз;
, 
, 
- коэффициенты мощности отдельных фаз;
, 
, 
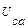- фазные напряжения;
, 
, 
- фазные токи.
При симметричной нагрузке фаз и симметричной системе напряжений
;
;
.
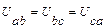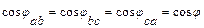Активная мощность трехфазного тока равна
.
Так как при соединении треугольником
и 
,
то
, Вт.
Аналогично определяют реактивную и полную мощности
, вар;
, в 
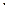а.
в случае чисто активной нагрузки 
(т.к. 
);
тогда 
; 
.
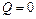ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с аппаратурой и приборами, необходимыми для выполнения работы, записать их технические данные в табл.4.1.
Таблица 4.1
Техническая характеристика приборов и аппаратов
| Наименование прибора | Система прибора | Класс точности | Пределы измерений | Цена деления |
2. Собрать схему, изображённую на рис.4.9, и дать её проверить преподавателю.
Рис. 4.9. Схема соединения приемников электроэнергии «треугольником»
3. Установить на приборах максимальные пределы измерения, включить схему.
4. Изменяя нагрузку в фазе аb включением ламп, снять показания приборов и записать их в таблицу 4.2.
5. Установить симметричную нагрузку фаз, отсоединить один из линейных проводов (например, лин. провод А) и записать показания приборов.
Таблица 4.2
Экспериментальные данные
| № | Кол-во эл.ламп в фазах | Режим нагрузки | Результаты измерений | ||||||||||
| ab | bc | ca |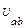 
| 
| 
| 
| 
| 
| 
| 
| 
| ||
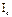
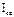
| В | В | В | А | А | А | А | А | А | |||||
| Несиммет-ричная | |||||||||||||
| Несиммет-ричная | |||||||||||||
| Симмет-ричная | |||||||||||||
| Несиммет-ричная | |||||||||||||
| Симмет-ричная |
6. Показать результаты опытов руководителю.
7. Разобрать схему, привести в порядок рабочее место.
8. Составить отчет о работе.
Отчет должен содержать следующие основные разделы:
- цель работы;
- схему опытной установки;
- техническую характеристику приборов и аппаратов;
- таблицу измерений;
- векторные диаграммы напряжений и токов для всех режимов нагрузки (табл.4.2);
- выводы.
контрольные вопросы
1. Что представляет собой трехфазная цепь с симметричными пассивными приемниками? Соединение «треугольником».
2. Что представляет собой трехфазная цепь с несимметричными пассивными приемниками? Соединение «треугольником», трехпроводная цепь.
3. Определить активную, реактивную и полную мощности приемников, соединенных «треугольником», при любом роде нагрузки.
4. Как изменяются электрические величины (напряжение, ток, мощность) при включении одной и той же трехфазной нагрузки по схеме «звезда» и «треугольник»?
5. Каковы будут напряжения на фазах приемников, если перегорит предохранитель в одном из линейных проводов или произойдет обрыв цепи линейного провода (нагрузка фаз симметричная)?
6. Построить векторную диаграмму токов и напряжений при симметричной нагрузке (табл.4.2, пункт 3).
7. Построить векторные диаграммы токов и напряжений при несимметричной нагрузке в случае обрыва цепи одной фазы
(табл.4.2, пункт 1).
8. Построить векторную диаграмму токов и напряжений при симметричной нагрузке, в случае обрыва цепи линейного провода (табл.4.2, пункт 5).
ЛАБОРАТОРНАЯ РАБОТА №5
