Поскольку данная функция элементарная и определена на всей числовой оси, то она непрерывна на всей числовой оси.
Для определения нулей функции решаем уравнение 
; 2x+3=0; 
.
Интервалы знакопостоянства функции.
Функция может изменить знак только в одной точке . Определим интервалы знакопостоянства функции.
| x | 
| 
|
| y | - | + |
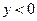при 
.
при 
.
Найдем точки пересечения с осями:
y=3 при x=0, следовательно 
- точка пересечения с осью 
.
при 
, следовательно 
- точка пересечения с осью 
Асимптоты графика функции.
А. Вертикальные асимптоты.
Поскольку функция непрерывна на всей числовой оси, то вертикальных асимптот нет.
Б. Наклонные асимптоты.
Учитывая разное поведение функции 
при 
и при 
, будем искать асимптоты по отдельности для и .
.
.
Отметим, что во втором пределе присутствует неопределенность вида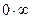 
, которую мы обратили в неопределенность вида 
. Далее предел вычисляется по правилу Лопиталя, в соответствии с которым предел отношения при наличии неопределенности равен пределу отношения производных числителя и знаменателя. Итак, при график исследуемой функции имеет горизонтальную асимптоту, совпадающую с осью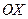 
: y=0.
Выясним, существует ли наклонная асимптота при .
Поскольку коэффициент k не имеет конечного значения, делаем вывод о том, что график не имеет наклонной асимптоты при .
Интервалы возрастания, убывания функции. Точки экстремума.
Находим производную:
, 
при 
.
Точек разрыва производная не имеет. Определяем интервалы знакопостоянства первой производной и интервалы возрастания и убывания функции. Производная может изменить знак в единственной точке . Составляем таблицу.
| x | 
| 
|
| y¢ | + | - |
| y | 
| 
|
Производная в точке меняет знак с плюса на минус. Следовательно точка является точкой максимума функции. Вычислим значение функции в этой точке. 
.
Выпуклость, вогнутость, точки перегиба графика функции.
Находим вторую производную
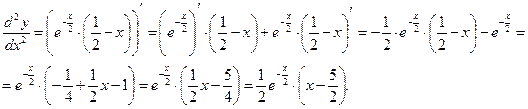
В области допустимых значений вторая производная точек разрыва не имеет. Вторая производная равна нулю при х=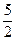 
.
Определяем интервалы знакопостоянства второй производной и интервалы выпуклости и вогнутости функции. Результаты сводим в таблицу.
| x |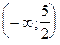 
| 
|
| y¢¢ | - | + |
| y | Ç | È |
Вторая производная меняет знак в точке х= 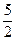, следовательно эта точка является точкой перегиба. Вычислим значение функции в этой точке. Имеем 
.
На основании проведенного исследования строим график функции.
ПРИЛОЖЕНИЕ
