Нули функции. Решаем уравнение y(x)=0. Имеем: 
=0; x=1. Следовательно, исследуемая функция обращается в ноль в единственной точке x=1.
Данная функция непрерывна на всей области допустимых значений.
Точка пересечения с осью Х, точка х=1.
Поскольку функция не определена при х=0, то ее график не пересекается с осью Y.
Интервалы знакопостоянства функции.
В области допустимых значений знак функции может меняться в единственной точке х=1. Точка х=1 разбивает область допустимых значений на два интервала (0;1) и (1; ¥). Определяем знак функции на каждом интервале и результаты сводим в таблицу:
| x | (0;1) | (1;+¥) |
| y | - | + |
Асимптоты графика функции.
А. Вертикальные асимптоты.
В своей области определения функция непрерывна. Поэтому асимптоты могут быть только на границе области определения.
. Итак, прямая х=0 – это вертикальная асимптота.
Б. Наклонные асимптоты.
. В этом пределе неопределенность вида 
. Применяем правило Лопиталя: 
. Поскольку k=0, то:
. (При вычислении предела использовано правило Лопиталя.)
Таким образом уравнение асимптоты при 
имеет вид
y=0.
Интервалы возрастания, убывания функции. Точки экстремума.
Находим производную:
= 
.
В области допустимых значений производная не имеет точек разрыва.
Нули производной находим, решая уравнение =0; 
; 
.
Точка разбивает область допустимых значений на два интервала 
и 
. Определяем знаки производной на каждом интервале и по знакам производной определяем интервалы возрастания и убывания функции. Результаты сводим в таблицу.
| x | (0;  )
| (;+¥)
|
| y¢ | + | - |
  y
|
В точке производная меняет знак с плюса на минус. Значит, точка является точкой максимума функции. Вычислим значение функции в этой точке. Имеем 
.
Выпуклость, вогнутость, точки перегиба графика функции.
Находим вторую производную
.
В области допустимых значений вторая производная точек разрыва не имеет. Для определения точек, в которых она равна нулю, решаем уравнение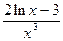 
=0; 
; 
; 
.
Определяем интервалы знакопостоянства второй производной и интервалы выпуклости и вогнутости функции. Результаты сводим в таблицу.
| x | (0;   )
| ( ;+¥)
|
| y¢¢ | - | + |
| y | Ç | È |
Вторая производная меняет знак в точке х= , следовательно, эта точка является точкой перегиба. Вычислим значение функции в этой точке. Имеем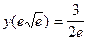 
.
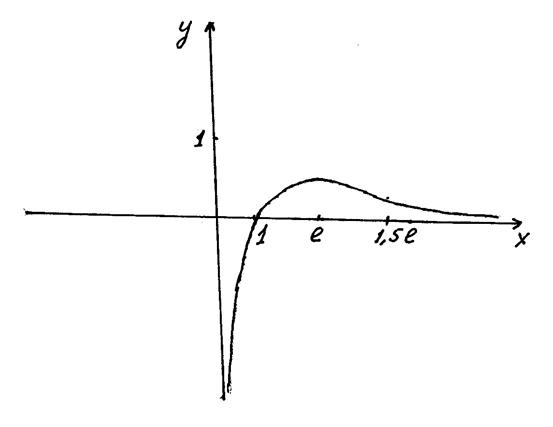
На основании проведенного исследования строим график функции.
Задача.
Методами дифференциального исчисления провести полное исследование функции и построить ее график: 
.
Решение.
1. Область определения данной функции – вся числовая ось.
Четность, нечетность функции.
Имеем 
. Данная функция не является ни четной, ни нечетной.
