Напомним некоторые понятия.
Функция называется выпуклой (вогнутой) на некотором интервале, если ее график лежит ниже (выше) касательной, проведенной в любой точке этого интервала.
Сформулируем достаточные условия. Если вторая производная функции отрицательна (положительна) на интервале, то данная функция является выпуклой (вогнутой) на этом интервале.
Точкой перегиба называется такая точка графика, в которой существует касательная, и в окрестности которой график функции лежит по разные стороны касательной. Точка перегиба отделяет выпуклую часть графика от вогнутой.
Достаточные условия точки перегиба формулируются следующим образом. Если в некоторой точке определена первая производная и при переходе через эту точку вторая производная меняет свой знак, то такая точка является абсциссой точки перегиба.
Находим вторую производную. 
= 
= 
.
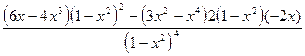Находим нули и точки разрыва второй производной, интервалы знакопостоянства второй производной. Определяем интервалы выпуклости и вогнутости функции.
Вторая производная равна нулю только в одной точке: х=0.
Вторая производная имеет точку разрыва в точках: х=-1, х=1.
Как и в предыдущем случае определяем интервалы знакопостоянства, и по знаку второй производной делаем вывод о выпуклости или вогнутости функции. Результаты удобно свести в таблицу. В таблице выпуклость функции будем обозначать символическим знаком Ç, вогнутость знаком È.
| х | (-¥;-1) | (-1;0) | (0;1) | (1;+ ¥) |
| у¢¢ | + | - | + | - |
| у | È | Ç | È | Ç |
Определим точки перегиба.
Вторая производная меняет знак в точках: х=-1; х=0; х=1.
Однако в точках х=-1 и х=1 функция не определена. Поэтому точкой перегиба является единственная точка х=0. Значение функции в этой точке у(0)=0.
С учетом исследования на выпуклость и вогнутость подправляем полученный ранее график плавной кривой. Таким образом, получаем окончательный вид графика функции.
В заключение заметим, что полученный график является лишь сжатой и наглядной формой сводки результатов исследования функции. Этот график можно еще уточнять. В тоже время, найденные асимптоты позволяют судить о поведении графика за пределами области изображения на приведенном рисунке.
Задача.
Методами дифференциального исчисления провести полное исследование функции и построить ее график: 
.
Область определения функции.
Функция определена при x>0.
Четность, нечетность функции.
Поскольку функция не определена при x 
0, то данная функция является функцией общего вида.
