На рис. 3.30 – 3.34 показаны результаты моделирования движения системы в двух случаях управления: (1) с помощью НР, БЗ которого была построена с использованием разработанного ОБЗ; и (2) с помощью классического ПИД-регулятора с постоянными коэффициентами усиления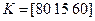 
, полученными усреднением коэффициентов усиления НР.
Примечание. На рис.3.30 – 3.34 использованы следующие обозначения: X – pendulum angle – угол отклонения маятника; Z – cart position – положение каретки; control error – ошибка управления; control force – управляющая сила; 
- производство энтропии в ОУ; 
- производство энтропии в регуляторе;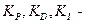 
коэффициенты усиления ПИД-регулятора.
Результаты моделирования показывают следующее
С точки зрения оптимизации ИСУ по критериям качества управления, таким как: минимум ошибки управления; минимум производства энтропии в объекте управления (т.е. минимум тепловых потерь, потерь полезной работы и энергии), а также с учетом ограничений на управляющую силу – ИСУ, разработанная на основе ОБЗ, эффективнее традиционных ПИД-регуляторов.
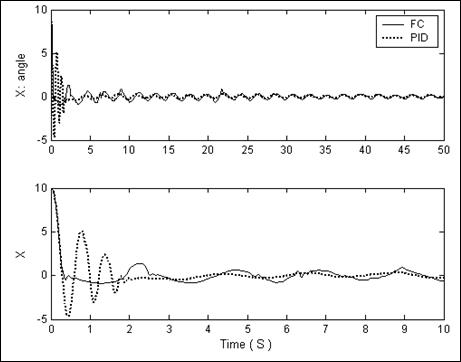
Рис. 3.30. Сравнение результатов моделирования управления ОУ с помощью НР (FC) и традиционного ПИД (PID)-регулятора. Движение маятника
Рис. 3.31. Сравнение результатов моделирования управления ОУ с помощью НР (FC) и традиционного ПИД (PID)-регулятора. Движение маятника и каретки
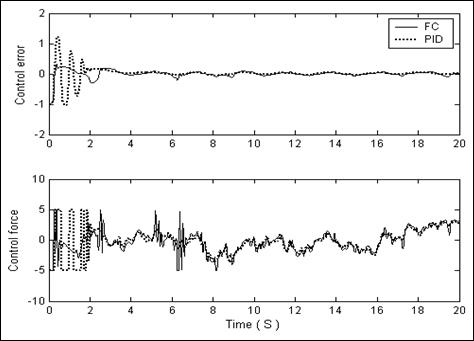
Рис. 3.32. Сравнение результатов моделирования управления ОУ с помощью НР (FC) и традиционного ПИД (PID)-регулятора. Ошибка управления и управляющая сила
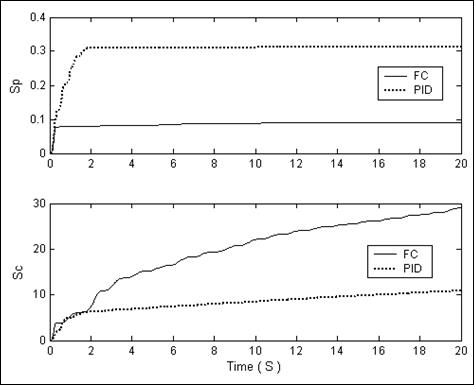
Рис. 3.33. Сравнение результатов моделирования производства энтропии в ОУ, НР (FC) и в традиционном ПИД (PID)-регулятора. Производство энтропии
Рис. 3.34. Законы управления коэффициентами усиления нечёткого и усреднённого ПИД (PID)-регулятора.
Исследование робастности построенной БЗ
Исследуем теперь свойство робастности построенной БЗ НР, управляющего движением перевернутого маятника.
Рассмотрим задачу управления с новыми условиями, отличную от первоначальной задачи управления, для которой подбирался оптимальный обучающий сигнал, и сравним результаты моделирования.
Задача управления с новыми условиями:
· другой шум, воздействующий на ОУ (отличный от обучающей ситуации): равномерно распределённый случайный процесс (рис. 3.35);
· другое время задержки в системе измерения = 0.002 сек.
На рис. 3.36 – 3.39 показаны результаты моделирования движения системы в новой (непредвиденной) ситуации управления.
Сравнение дается для двух случаев управления: (1) с помощью НР, БЗ которого была построена с использованием разработанного ОБЗ; и (2) с помощью классического ПИД-регулятора с коэффициентами усиления 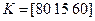, полученными усреднением коэффициентов усиления НР.
На рис. 3.36 дано сравнение результатов движения маятника и каретки перемещения; на рис. 3.37 показано сравнение управляющей силы; на рис. 3.38 сравниваются термодинамические характеристики ОУ и регуляторов (потери полезной работы) в соответствии с уравнением (2.3); и на рис.3.39 показаны законы управления коэффициентами усиления нечеткого и традиционного ПИД-регуляторов.
Рис. 3.35. Равномерно распределённый случайный процесс
Рис. 3.36. Сравнение результатов моделирования управления ОУ с помощью НР (FC) и традиционного ПИД (PID)-регулятора (новая ситуация управления). Движение маятника и каретки
Рис. 3.37 Сравнение результатов моделирования управления ОУ с помощью НР (FC) и традиционного ПИД (PID)-регулятора (новая ситуация управления).
Ошибка управления и управляющая сила
Рис. 3.38 Сравнение результатов моделирования производства энтропии в ОУ, НР (FC) и традиционном ПИД (PID)-регулятора (новая ситуация управления).
Производство энтропии
Рис. 3.39. Законы управления коэффициентами усиления нечёткого и усреднённогоПИД (PID)-регулятора (новая ситуация управления).
Результаты моделирования показывают:
· построенная БЗ НР, управляющего движением перевернутого маятника, является робастной;
· с точки зрения критериев качества управления таких, как минимум ошибки управления; минимум производства энтропии в объекте управления и системе управления (т.е. минимум тепловых потерь и потерь полезной работы и энергии), а также с учетом минимума управляющей силы разработанная на основе ОБЗ ИСУ эффективнее традиционных ПИД-регуляторов с постоянными коэффициентами усиления.
Общие выводы
· Разработанный инструментарий, основанный на мягких вычислениях и стохастическом моделировании, является эффективным инструментом для извлечения объективной БЗ НК (не зависящей от субъективных знаний эксперта). Он базируется на объективных физических и механических законах, описывающих динамическое поведение объекта управления.
· Такой подход с применением разработанного программного продукта в виде ОБЗ позволяет: (1) осуществить принцип проектирования оптимальной ИСУ с максимальным уровнем надежности и управляемости сложным ОУ в условиях неопределенности исходной информации; (2) сократить до требуемого минимума необходимое количество датчиков сбора и передачи информации, как в контуре управления, так и в измерительной системе без потери точности и качества управления. Робастность ИСУ, полученная на основе такого подхода, требует минимума исходной информации, как о поведении ОУ, так и о внешних возмущениях.
В главе 5 эффективность применения ОБЗ демонстрируется на конкретных типовых примерах (т.н. “ Benchmarks ”) моделей ОУ.
В частности, исследуемые модели физических ОУ имеют следующие (типовые для реальных динамических ОУ) особенности: (1) по части обобщённых координат обладают локальной и глобальной динамической неустойчивостью; (2) по обобщённым динамическим координатам имеют существенно нелинейные перекрёстные связи (стохастические нелинейности), которые взаимно (антагонистично) влияют на динамику, устойчивость и управляемость ОУ; и (3) работают в непредвиденных ситуациях управления.
Рекомендуемая дополнительная литература к Главе 3
1. Litvintseva L.V., Ulyanov S.V. Takahashi K., Ulyanov S.S. Intelligent robust control design based on new types of computations. Part 1: New soft computing technology of KB-design Benchmarks of smart control simulation for nonlinear dynamic systems. – Universita degli Studi di Milano, Polo Didattico e di Ricerca di Crema Publ. – 2004. – Vol. 60.
2. Литвинцева Л.В., Ульянов С.В., Ульянов С.С. Проектирование робастных баз знаний нечетких регуляторов для интеллектуального управления существенно-нелинейными динамическими системами. Ч. II // Изв. РАН. ТиСУ. – 2006. – № 5. – С. 69–97.
Контрольные вопросы к Главе 3
1. Этапы проектирования БЗ
2. Термодинамическое распределение критериев качества управления
3. Роль генетических алгоритмов в структуре ОБЗ
