Обсудим прикладные аспекты использования и обоснование разработки данной ИТП ИСУ. Рассмотрим некоторую компанию, у которой возникла необходимость повысить качество и надёжность своих изделий. Пусть, например, основными изделиями компании являются мотоциклы, катера, снегоходы, скутеры, беспилотные вертолёты, холодильные установки, и т.п. Эффективность данных изделий во многом зависит от экономичности и надёжности работы в различных климатических условиях различных подсистем таких как, двигатель, подвеска автомобиля, система управления навигацией и т.д. В задачах повышения качества и конкурентоспособности таких изделий основную роль играют встроенные в изделие интегрированные системы управления (например, двигателем, подвеской, системой навигации и др.).
Для эффективного управления подобными объектами требуется интегрированная ИСУ, позволяющая поддерживать необходимые критерии качества управления на требуемом уровне.
На рисунке 3.7 показан обобщённый конструктивный подход к построению возможных путей решения задачи по повышению качеств выпускаемой продукции некоторой компанией.
Как видно из рис. 3.7, одним из путей решения поставленной задачи является создание новой ИТП ИСУ, основанной на новых видах вычислений, и соответствующей аппаратно программной поддержки соответствующих этапов процесса проектирования.
С точки зрения разрабатываемой технологии выпускаемое изделие должно рассматриваться как физический ОУ с предъявляемыми к нему критериями качества управления, которые должны быть описаны и формализованы на языке теории систем управления. Следовательно, необходимо определить, какие критерии качества управления соответствуют требованиям поставленных задач компанией.
Рассмотрим следующие качества управления: управляемость, устойчивость, адаптация, робастность.
Выберем простую систему управления, которая объединяет в себе максимальное количество критериев качества управления, т.е. устойчивость, точность управления управляемость, гарантируя определённый уровень робастности. В качестве таковой системы (нижний уровень управления) выберем классический ПИД-регулятор.
Для того, что бы повысить уровень робастности системы нижнего уровня будем строить ИСУ в виде нечеткого контроллера (НК) с учетом принципа не разрушения нижнего уровня управления.
В теории автоматического регулирования известны два основных принципа управления:
1) Глобальная отрицательная обратная связь (ГООС);
2) Принцип минимума ошибки управления.
Первый принцип обеспечивает устойчивость динамического объекта управления (ОУ). Принцип минимума ошибки управления обеспечивает управляемость ОУ.
При этом критерии качества управления такие как, устойчивость и управляемость находятся в противоречии: а именно увеличение одного качества управления приводит к уменьшению другого качества управления.
Обеспечение равновесия между двумя противоречиями критерий качества управления осуществляется методами проектирования оптимального регулятора, позволяющие ввести в неявном виде критерии динамического поведения ОУ.
Аналитическое конструирование оптимального регулятора, обеспечивающее в общем виде требуемый уровень робастности существенно нелинейных ОУ, является алгоритмически неразрешимой проблемой.
Для решения этой проблемы был разработан новый принцип глобальной интеллектуальной обратной связи (ГИОС) для извлечения, обработки и формирования БЗ НК, с помощью которого осуществляется оптимальное управление коэффициентами усиления традиционного регулятора и достигается требуемый уровень робастности.
Таким образом, используя отрицательную обратную связь можно добиться только устойчивости и управляемости. Применив интеллектуальную обратную связь, мы добились возможности ввести новый критерий качества управления – робастность - и контролировать уровень робастности за счёт формирования (проектирования) соответствующего уровня интеллектуальности БЗ.
Данный комбинированный принцип управления (сочетание двух обратных связей [ГООС и ГИОС]), позволяет реализовать принцип не разрушения нижнего уровня системы управления, используя его достоинства на верхнем уровне управления.
Важнейшим элементом в данной структуре управления является понятие ГИОС.
1) Введение понятия ГИОС позволяет извлекать ценную информацию об индивидуальном поведении регулятора и ОУ, формируя тем самым процесс извлечения знаний о динамическом поведении регулятора (сигнал управления) и динамическом поведении ОУ.
2) Введение новых типов вычислений (таких как мягкие, квантовые и квантовые мягкие вычисления) позволяют осуществить процесс обработки извлечённых знаний.
3) Введение процессов оптимизации обработанных знаний позволяет осуществить процесс формирования знаний в виде робастных БЗ НК.
Таким образом, извлечение, обработка и формирование знаний (как основная проблема теории искусственного интеллекта) отражены и включены в ИТП ИСУ.
Поскольку как отмечалось выше, понятие ГИОС позволяет ввести такой критерий качества как робастность, то на конечном этапе формирования обработанных знаний имеется возможность спроектировать требуемый уровень интеллектуальности БЗ, обеспечивающий необходимый уровень робастности управления.
3.2.1.1 Особенности инструментария ОБЗ
Для проектирования робастных БЗ ИСУ был разработан инструментарий на мягких и квантовых вычислениях, позволяющий проектировать необходимый уровень робастности.
Подробно он описывается во всех последующих главах, а здесь мы обсудим его особенности.
Для ускоренного интегрирования существенно нелинейных уравнений высокого порядка, описывающих динамическое поведение ОУ с большим числом степеней свободы, потребовался ускоренный метод интегрирования таких уравнений без потери точности численного интегрирования по сравнению с традиционными алгоритмами (таких как Рунга- Кутта, Адамса и т.д.).
Это также связано с необходимостью формировать функцию пригодности для ГА осуществляющего обработку извлечённых знаний.
Оптимизация по функции пригодности (сформированная с данным поведением регулятора и ОУ) позволяет, как результат обработки сформировать обучающий сигнал.
Дополнительная обработка обучающего сигнала на основе оптимизаторов с новыми видами вычислений, позволяет сформировать БЗ НК с требуемым уровнем интеллектуальности, который в свою очередь обеспечивает достижение проектируемого уровня робастности управления.
Важнейшими компонентами ИТП ИСУ являются различные структуры ГА с дискретными ограничениями и Оптимизатор Знаний на новых видах вычислений.
Совместные действия этих компонент обеспечивают извлечение, обработку и формирование знаний, решая одну из актуальных проблем теории искусственного интеллекта, как базиса проектирования ИСУ.
В заключение перечислим ключевые факторы ИТП ИСУ:
1. Вводится новый критерий качества управления – робастность.
2. Взаимодействие двух связей ГООС и ГИОС даёт принцип не разрушения нижнего уровня системы управления.
3. В случае необходимости учета дополнительного критерия качества управления при существующих критериях (например, устойчивости и управляемости), то необходимо использовать новые виды вычислений.
Введение ГИОС позволило реализовать три этапа работы со знаниями:
1. извлекать информацию из динамического поведения традиционного регулятора и ОУ;
2. обрабатывать полученную информацию с помощью ГА и функции пригодности, вырабатывая на выходе обучающий сигнал;
3. формировать знания в виде робастной БЗ с помощью соответствующего класса ГА, использующих различные типы функций пригодности.
Выполнение этих трёх этапов работы со знаниями позволяет через спроектированный уровень интеллектуальности БЗ задать соответствующий уровень робастности. Таким образом, вся проблема сконцентрирована в разработке технологии проектирования БЗ с соответствующим уровнем интеллектуальности.
Этапы ИТП ИСУ
В этом разделе мы подробно опишем шаги информационной технологии проектирования ИСУ на основе разработанного инструментария ОБЗ. Как было показано выше, такие ИСУ входят в класс интеллектуальных нечетких регуляторов (НР) с различным нижним исполнительным уровнем.
На рис. 3.9 показаны основные этапы проектирования в разработанной нами ИТП ИСУ на основе мягких вычислений.
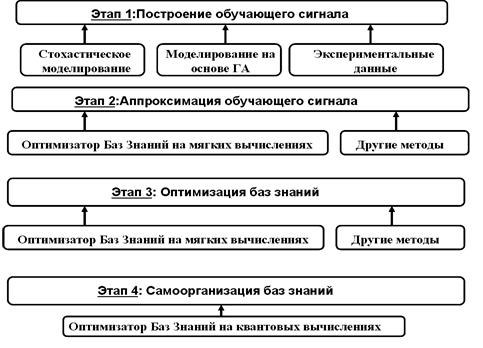
Рис. 3.9. Основные стадии ИТП ИСУ
Примечание. Этап 4 на рис.3.9 изложен в Части 2 данной книги.
3.2.2.1. Извлечение, обработка и формирование объективных знаний на основе технологий мягких вычислений и стохастического моделирования
Опишем основные этапы технологии, основанные на методах мягких вычислений и стохастического моделирования, для построения НР и их БЗ. Вначале опишем кратко стадии 1-3 (рис.3.9), а затем рассмотрим их более подробно на примерах выбранных ОУ.
В соответствии со схемой на рис.3.10 процесс построения БЗ может быть реализован следующими этапами.
Этап 0. Пользователь формирует адекватную для его задачи управления модель нечеткого вывода. Для этого он должен выбрать: тип нечеткой модели и интерпретацию используемых в ней нечетких операций; а также число входных и выходных переменных.
Рис. 3.10. Этапы проектирования БЗ НР
Например, пользователь конкретизирует тип нечеткой модели вывода как Сугено 0, операцию нечеткой конъюнкции как произведение, и задает число входных и выходных переменных. Пусть 
есть количество функций принадлежности, описывающих ошибку управления е, ее скорость и интеграл, тогда общее число нечетких правил будет 
.
Само нечеткое (продукционное) правило в БЗ выглядит следующим образом:
где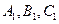 
- функции принадлежности, описывающие ошибку управления е, ее скорость и интегральную часть, 
– числа.
Тогда конечный результат нечеткого вывода в заданной БЗ будет вычисляться по следующим формулам:
;
,
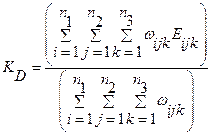где 
, «∙» - символ операции нечеткого умножения.
На данном этапе определяются один (или несколько) типовых ситуаций обучения, в которые входят следующие факторы:
· параметры модели объекта управления;
· начальные данные;
· задающий сигнал;
· внешний шум;
· наличие или отсутствие времени задержки в канале измерения состояния ОУ.
Для построения робастных БЗ мы будем использовать систему стохастического моделирования для того, чтобы найти робастныйобучающий сигнал.
Этап 1. Система стохастического моделирования для построения обучающего сигнала
Стохастическое моделирование основано на процессе извлечения информации из исследования индивидуальных информативных траекторий, описывающих динамическое поведение ОУ при воздействии на него случайных процессов (внешних и внутренних шумов).
В рамках корреляционной теории различные по своей статистической природе случайные процессы (т.е. имеющие различные функции плотности распределения вероятности) могут быть неразличимыми по своим корреляционным свойствам. Полной статистической характеристикой случайных процессов является функция плотности распределения вероятностей.
Поэтому выходной процесс формирующего фильтра, моделирующего внешнюю среду, должен быть представительной информативно значимой выборочной траекторией случайного процесса, позволяющий исследовать индивидуальные траектории динамических нечётких систем. Этому требованию удовлетворяют выборочные траектории случайных процессов, если известна их функция плотности распределения вероятностей.
Моделирование случайных процессов с требуемой функцией плотности распределения вероятностей осуществляется методом формирующих фильтров. В данном разделе используется методология проектирования структур ИСУ функционирующих во внешней среде при наличии случайных процессов, имеющих одинаковую автокорреляционную функцию и различные функции распределения плотности вероятностей.
Метод формирующих фильтров для описания случайных процессов с требуемой функцией плотности распределения вероятностей на основе уравнений Фоккера-Планка-Колмогорова описан в Приложении к данной Главе 3.
На рис. 3.11 показаны примеры внешних шумов с различной стохастической природой (функциями плотности распределения вероятностей).
Рис. 3.11 Вид функций плотности распределения вероятностей и результаты моделирования выходных случайных процессов от соответствующих формирующих фильтров: (1) – Гауссовский случайный процесс; (2)– Рэлеевский случайный процесс; (3)– равномерно распределённый случайный процесс.
Система стохастического моделирования предназначена для извлечения объективных знаний об управлении динамическим поведением ОУ с использованием сгенерированных внешних стохастических шумов и ГА с выбранной функцией пригодности (ФП) для поиска оптимального управления
Рис. 3.12. Структура системы стохастического моделирования
На рис. 3.12 указаны основные факторы, влияющие на чувствительность и надёжность точности управления. К ним относятся: внешние и внутренние шумы, задержки по времени и шумы в измерительной системе, а также неточности в определении параметров модели, неполнота обучающих факторов и др.
Входом в систему стохастического моделирования является вектор ошибки управления, а выходом системы является обучающий сигнал (ОС), представляющий собой таблицу следующих входных/выходных данных:
где 
- вектор, компонентами которого является ошибка управления, ее производная и интеграл соответственно,
а 
– параметры ПИД регулятора в момент времени 
.
3.2.2.1 Методология стохастического моделирования для этапа 1 ИТП ИСУ
Задачей на данном этапе является исследование динамического и термодинамического поведения ОУ в присутствии различных факторов: внешние и внутренние шумы; погрешности в каналах измерения состояния объекта, неполнота и неточность модельных параметров и др. Исследование состоит из следующих шагов.
1) Исследование свободного движения ОУ
На первом шаге исследуется свободное движение ОУ, его динамическое и термодинамической поведение при различных начальных данных и различных параметрах модели в отсутствии внешних воздействий. В результате этого шага определяется тип поведения динамического объекта (устойчивый или неустойчивый глобально или локально).
2) Исследование стохастического движения ОУ
На данном шаге рассматривается динамическое и термодинамической поведение ОУ при стохастическом внешнем воздействии различной природы (рис.3.11). При этом исследуется влияние типа шума на локальную или глобальную неустойчивость ОУ.
3) Исследование стохастического движения ОУ при классическом управлении на основе П(И)Д регуляторов
На данном этапе изучается динамическое и термодинамической поведение ОУ при стохастическом внешнем воздействии и при заданном типе классического управления на основе ПИД регуляторов с постоянными коэффициентами усиления в типовых условиях функционирования ОУ.
Примечание. Напомним формулу вычисления силы управления при ПИД управлении:
,
где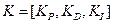 
- постоянные коэффициенты усиления.
На данном шаге находятся области изменения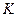 
, исследуется влияние различных шумов и других факторов, таких как, задержка по времени в канале системы измерения на качество управления и определяются физические ограничения классических регуляторов в решении задачи управления выбранным ОУ. В результате мы выбираем структуру управления нижнего уровня (ПИД- или ПД- или П-регулятор) для дальнейшего проектирования ИСУ на основе нечеткого регулятора (НР).
4) Построение обучающего сигнала
Для заданной типовой ситуации с помощью ГА, выбранной функции пригодности и выбранной области поиска для значений 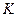, мы находим близкое к оптимуму решение 
где - моменты времени управления.
Функция пригодности (ФП) описывает выбранный физический критерий оптимизации, например, минимум ошибки управления, или минимум ошибки управления и ее скорости, или минимум обобщенного производства энтропии и т.д. В некоторых более сложных случаях ФП может включать некоторую взвешенную сумму различных характеристик движения ОУ, например его скорость, ускорение или термодинамические характеристики.
Система стохастического моделирования реализована в среде Матлаб/ Симулинк, ее структура показана на рисунке 3.13 и состоит из следующих компонент:
1. Подсистема с уравнениями движения динамического ОУ (на рисунке это «Control Object»:
2. Подсистема моделирования качества управления (на рисунке это «Simulation system of control quality» (SSCQ)), которая представляет собой С++ реализацию ГА;
3. Блок генерации задающего сигнала управления. В зависимости от задач управления это может быть некоторый статичный сигнал (константа) или переменный сигнал, описывающий заданную траекторию;
4. Блок ПИД регулятора (на рисунке это «PID controller») с переменными коэффициентами усиления. Данный блок имеет два выхода: сила управления и вектор ошибки управления;
5. Блок «Селектор» (Selector) для выбора той переменной движения ОУ, которая находится под управлением.
Блок SSCQ реализован как C++ Simulink S-Function, содержащий:
· Уравнения движения ОУ;
· ГА;
· Интегратор на основе метода Рунге-Кутта с фиксированным шагом (Fixed step Runge-Kutta (R-K) integrator);
· Описание области поиска для ГА;
· Блок описания ФП.
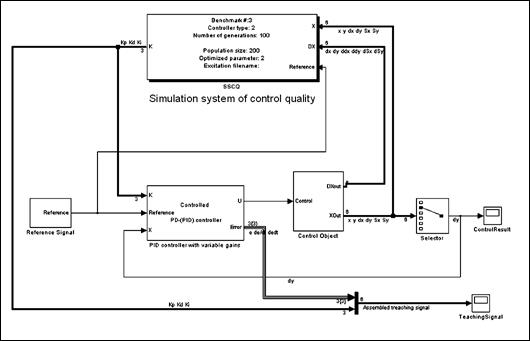
Рис 3.13. Матлаб-Симулинк структура системы стохастического моделирования
Выходом системы стохастического моделирования является обучающий сигнал в виде:
,
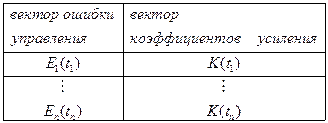где 
и 
.
Обучающий сигнал поступает на вход следующего этапа 2, на котором используется инструментарий ОБЗ.
В заключение подчеркнем основные черты системы стохастического моделирования:
· для генерации стохастических внешних шумов мы используем метод формирующих фильтров с требуемой функцией плотности распределения вероятностей на основе уравнений Фоккера-Планка-Колмогорова;
· для построения ОС оптимального управления используется ГА с выбранной ФП и математическая модель (или физическая модель) ОУ;
· в качестве ФП используются различные функции: минимум ошибки управления, или минимум ошибки управления и ее скорости; кроме того могут использоваться термодинамические характеристики ОУ такие, как его скорость, ускорение или минимум производства обобщенной энтропии системы «ОУ+ система управления».
· с помощью стохастического моделирования создается ансамбль выборочных траекторий «рандомизированного» поведения ОУ, а с помощью принципов нечеткого моделирования на основе мягких вычислений осуществляется качественный анализ и извлечение знаний из выборочной траектории с целью формирования БЗ нечеткого контроллера в соответствии с заданным функционалом качества (функции пригодности ГА).
3.2.2.2. Аппроксимация обучающего сигнала с помощью ОБЗ
Этап 2. Обучающий сигнал, сформированный на этапе 1, подается на вход ОБЗ, который аппроксимирует его с помощью заданной пользователем (этап 0) модели нечеткого вывода, используя разработанный инструментарий.
ОБЗ на мягких вычислениях является новым эффективным программным инструментарием построения БЗ робастных ИСУ с использованием новых критериев оптимизации (в виде новых типов функций пригодности ГА). В качестве таковых используются термодинамические и информационно-энтропийные критерии, представленные в Таблице 3.2.
Таблица 3.2.
Типы и роль функции пригодности ГА в ОБЗ
| Тип ГА | Критерии | ФП | Роль ФП |
| ГА1: Оптимизация лингвистических переменных | Максимумсовместной информационной энтропии. Минимуминформации о сигналах в отдельности |  где 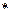 выбранная операция нечёткой конъюнкции.
| Выбор оптимальной мощности терм-множеств лингвистических переменных компонент ОС. Устранение избыточности ОС; |
| |||
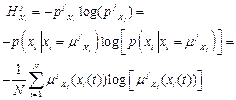
| ГА2: Оптимизация базы правил | Минимумошибки аппроксимации |  ,
где 
| Выбор оптимальных параметров правых частей правил |
| ГА3: Настройка БЗ | Минимум ошибки аппроксимации или Максимумсовместной информационной энтропии |
| «Тонкая» настройка параметров функций принадлежности |
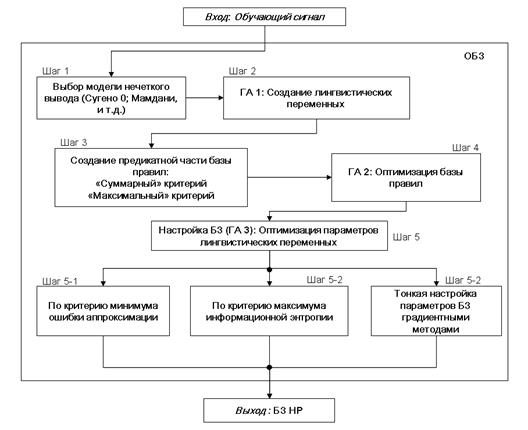
Рис. 3.14. Структура ОБЗ и шаги оптимизации БЗ
Примечание. В Таблице 3.2 представлены функции пригодности для трех ГА алгоритмов, использующихся в ОБЗ. Каждая функция пригодности ФП представляет соответствующий критерий. В таблице описывается также роль выбранной ФП на данном шаге вычисления.
ОБЗ состоит из взаимосвязанных генетических алгоритмов (ГА1, ГА2, ГА3), оптимизирующих отдельные компоненты БЗ.
Структура и шаги оптимизации представлены на рис. 3.14.
Входом ОБЗ является обучающий сигнал (ОС), который может быть получен либо на этапе стохастического моделирования поведения ОУ (с использованием его математической модели), либо экспериментально, т.е. непосредственно из измерений динамических параметров физической модели ОУ.
Специфицируем шаги алгоритма оптимизации.
Шаг 1: Выбор модели нечёткого вывода. Пользователь определяет тип нечёткой модели вывода (Сугено, Мамдани, и т.д.), и число входных и выходных переменных.
Шаг 2: Создание лингвистических переменных. С помощью ГА1 определяется оптимальное число функций принадлежности для каждой входной лингвистической переменной, а также выбирается оптимальная форма представления ее функций принадлежности (треугольная, Гауссовская и т.д.).
Шаг 3: Создание базы правил. На данном этапе используется специальный алгоритм отбора наиболее «робастных правил» в соответствии со следующими двумя критериями:
1) «суммарный» критерий: выбрать только те правила, которые удовлетворяют следующему условию:
,
где TL (threshold level) - заданный (вручную или выбранный автоматически) уровень активации правила, и
, 
,
где 
моменты времени, 
,
N равно числу точек в управляющем сигнале;
- функции принадлежности входных переменных,
- индекс правила в БЗ; символ «
» обозначает операцию нечеткой конъюнкции (в частности, может интерпретироваться как произведение).
2) «максимальный» критерий: выбрать только те правила, которые удовлетворяют условию:
.
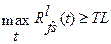Шаг 4: Оптимизация базы правил. С помощью ГА2 оптимизируются правые части правил БЗ, определенной на шаге 3. На данном этапе находится решение, близкое к глобальному оптимуму (минимум ошибки аппроксимации ОС). С помощью следующего шага это решение может быть локально улучшено.
Шаг 5: Настройка базы правил. С помощью ГА3 оптимизируются левые и правые части правил БЗ, т.е. подбираются оптимальные параметры функций принадлежности входных/выходных переменных (с точки зрения заданной функции пригодности ГА). В данном процессе оптимизации используются различные функции пригодности, выбранные пользователем (шаги 5-1, 5-2 на рис. 3.14). На данном этапе имеется также возможность настройки БЗ с помощью традиционного метода обратного распространения ошибки (см. шаг 5-3 на рис.3.14).
Результатом аппроксимации ОС является построенная БЗ НР (база знаний нечеткого регулятора), включающая множество правил и оптимально сформированные параметры функции принадлежности входных и выходных переменных НР.
Верификация (тестирование) построенной БЗ. Построенные БЗ ИСУ тестируются с точки зрения робастности и качества управления. Для дальнейшего использования выбирается функционально наилучшая БЗ, которая апробируется в режиме функционирования в реальном времени.
Этап 3. Разработанный на этапе 2 НР тестируется с помощью системы моделирования движения ОУ (или в реальном приложении). Если результаты тестирования удовлетворяют требованиям качества проектирования, то разработанный НР может использоваться в режиме реального времени. Если результаты моделирования не удовлетворительны, этапы 0-3 должны быть повторены с другими ФП в ГА.
Рассмотрим более подробно алгоритмы указанных шагов проектирования и оптимизации БЗ.
