ГА1 алгоритм генерации лингвистических переменных при построении баз знаний нечетких систем

В данном разделе рассматривается метод построения терм-множеств лингвистических переменных, по заданному обучающему сигналу, основанный на информационном анализе совместной плотности распределения элементов терм-множества лингвистической переменной. Предложенный способ позволяет определить тип и необходимое количество терм-множества, что позволяет применить к полученной структуре известные методы оптимизации.

Построение терм-множеств лингвистических переменных является важным этапом формирования БЗ нечетких систем, и в особенности, НР. Структура терм-множества лингвистической переменной характеризуется числом и типом функций принадлежности входящих характеризующих элементы терм-множества данной переменной.

В практике создания БЗ нечетких систем, построение терм- множества осуществляется экспертом на основании личного опыта, либо их структура итеративно подбирается, до достижения ее оптимальной структуры. Обычно в качестве критерия оптимальности выступает значение ошибки аппроксимации, вычисляемое как разница между желаемым значением выходного сигнала и значением, полученным в результате нечеткого вывода на заключительном этапе оптимизации параметров структуры нечеткой системы.

Таким образом, известные алгоритмы оптимизации должны быть применены итеративно к разным (изначально заданным) структурам лингвистических переменных. Затем полученные результаты сравниваются и выбирается наилучший вариант. Данный процесс требует больших вычислительных затрат, связанных с применением алгоритмов оптимизации, и во многих случаях (особенно при сложной структуре проектируемого регулятора) остается значительная вероятность появления ошибки второго рода, связанной с неоптимальной изначальной структурой терм-множеств лингвистических переменных.

Рассмотрим обучающий сигнал и его лингвистическое описание, представленные на рис. 3.15.

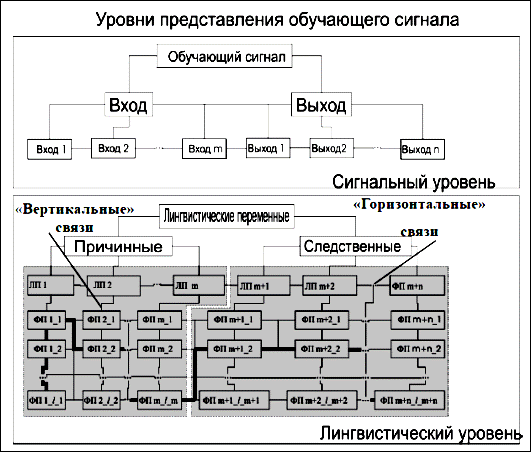
Рис. 3.15. Структура обучающего сигнала и его лингвистическое описание

На рис.3.15 зависимости между сигналами представлены графически горизонтальными и вертикальными линиями. Каждой из компонент сигнала соответствует некоторая лингвистическая переменная, описывающая сигнал с помощью лингвистические значения сигнала с помощью соответствующего терм-множества. Мощность терм множества и параметры составляющих его элементов (класс и параметры функции принадлежности) неизвестны. Полноту" лингвистического описания сигнала можно описать на уровне взаимосвязи терм-множеств, входящих в лингвистические переменные.

На рис.3.15 эти взаимосвязи представлены вертикальными и горизонтальными линиями, соединяющими терм-множества лингвистических переменных. Увеличение мощности терм-множеств ведет к увеличению числа возможных линий связи между элементами терм-множества лингвистических переменных. В результате этого большему числу состояний сигнала будут соответствовать более точные лингвистические значения. В пределе, если мощность терм множеств бесконечно, лингвистическое описание будет точно соответствовать числовым значениям. Меньшее число терм-множеств и соответственно вертикальных связей, огрубляет лингвистическое описание, что в большинстве случаев предпочтительнее с точки зрения увеличения робастности системы.

Определение требуемого соотношения между точностью описания и необходимой робастностью является очень важной задачей и на практике решается экспертными методами. Важно также отметить, что горизонтальные линии, соединяющие элементы терм-множеств разных лингвистических переменных, по сути являются компонентами продукционных правил, на основании которых лингвистическое описание связывается в систему нечеткого вывода.

Таким образом, выбор структуры лингвистических переменных косвенно влияет на объем и адекватность получаемой базы продукционных правил.

Рассмотрим информационный подход к оптимизации структуры лингвистических переменных. Данный подход является развитием результатов применительно к оптимизации нечетких систем.

Постановка задачи для шага 2.

Рассмотрим типичное продукционное правило системы нечеткого вывода Сугено, нулевого порядка:

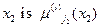IF AND AND … AND THEN ,

Результирующий вывод по нечетким правилам указанного типа, вычисляется по формуле:

(3.5)

Рассмотрим обучающий сигнал, представленный выборкой:

где: - порядковый номер элемента выборки; - число элементов в выборке; - компоненты входной составляющей обучающего сигнала; - компоненты выходной составляющей обучающего сигнала; , - число входных и выходных компонент сигнала соответственно.

Задача состоит в определении оптимального лингвистического описания сигналов. В качестве критерия оптимальности используется функция максимума вероятности вхождения компонент сигнала в различные элементы терм-множества лингвистической переменной. При минимальной мощности терм-множества, описывающего каждую компоненту сигнала.

Перейдем к формальному описанию задачи.

Для представления всех элементов, входящих в обучающую выборку, необходимо определить лингвистических переменных.

Пусть , и , есть набор лингвистических переменных, соответствующих входным и выходным составляющим обучающего сигнала. Тогда для каждой лингвистической переменной можно задать некоторое терм-множество. В результате вход-выход системы может быть представлен в следующем виде:

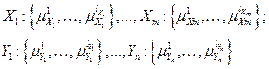Здесь терм-множество, соответствующее -й компоненте входного сигнала; терм-множество, соответствующее -й компоненте выходного сигнала.

На первоначальном этапе формирования БЗ, класс функций принадлежности и их параметры неизвестны. Неизвестны также мощности терм-множеств соответствующих лингвистических переменных.

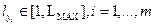Предположим, что является параметром, оптимизируемым некоторым генетическим алгоритмом, с диапазоном поиска: , . является максимально допустимым числом элементов терм-множества. На практике значение L_MAX определяется экспертным путем. Имея в результате оптимизации значения , можно построить равновероятностное распределение 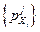характеризующее принятие -й компонентой обучающего значение в соответствующем терм множестве.

При этом выполняется условие:

(3.6)

Данное ограничение подобно разделению гистограммы сигнала на криволинейные трапеции одинаковой площади. При этом основания криволинейных трапеций задают носители соответствующих функций принадлежности. Пересечение двух соседних элементов терм-множества может задаваться некоторым коэффициентом, который является результатом работы генетического алгоритма. Этот коэффициент принимает значение 0 при пустом пересечении и большим нуля, когда пересечение не пусто.

На рис. 3.16 представлены варианты размещения треугольных функций принадлежности согласно введенному ограничению, для одного компонента обучающего сигнала, представленного на рис. 3.17.

(а)
(б
(в)
(г)

Рис. 3.16. Терм-множество лингвистической переменной для различных значений коэффициентов перекрытия пересечения элементов терм-множества: 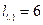; а) =0; б) =0.5; в) =1; г) Гистограмма сигнала, использованного при построении терм-множества.

Рис. 3.17. Обучающий сигнал, использованный для построения терм-множеств, представленных на рис. 3.16.

Модальные значения несимметричных нечетких множеств помещаются в наиболее вероятную точку, попадающую в основание криволинейной трапеции.

Примечание. - параметр, характеризующий область пересечения соседних терм-множеств.

Взаимосвязь между возможностью активации нечеткого множества в зависимости от значений его параметров можно выразить через вероятность его активации:

(3.7)

Исходя из геометрических соображений, совместную вероятность активации одновременно двух нечетких множеств можно рассчитать по формуле:

, (3.8)

где 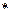обозначает выбранную логическую операцию нечеткого «И», или T-норму; - индексы соответствующих функций принадлежности.

Если , и , выражение (3.8) определяет “вертикальные связи”; если 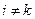- выражение (3.8) определяет “горизонтальные связи”. Мерой “вертикальных” и “горизонтальных” связей является совместная вероятность попадания значений сигнала в нечеткие множества, определяющие соответствующую связь.

Набор значений лингвистических переменных оптимален, если суммарная мера горизонтальных связей максимальна, при минимальном значении суммарной меры вертикальных связей.

Таким образом, можно определить функцию пригодности генетического алгоритма, оптимизирующего число и параметры функций принадлежности, как максимум меры (3.8) с учетом ограничения (3.6).

Для формирования системы оптимизации была принята следующая структура хромосомы:

, (3.9)

В формуле (3.9), – гены, кодирующие мощности терм множеств лингвистических переменных; - гены, кодирующие коэффициенты характеризующие пересечения носителей функций принадлежности соответствующей лингвистической переменной ; - гены, кодирующие класс функций принадлежности нечетких множеств.

Другой способ задания функций пригодности (3.7) и (3.8) может быть основан на энтропии Шеннона. В этом случае формулы (3.7) и (3.8) могут быть представлены в следующем виде:

(3.7a)

(3.8a)

В некоторых приложениях можно использовать комбинацию информационных и вероятностных мер. Результатом работы ГА является оптимизированная структура терм-множеств лингвистических переменных.