МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение
Высшего образования
«Севастопольский государственный университет»
МОРСКОЙ КОЛЛЕДЖ
ПРАКТИЧЕСКАЯ РАБОТА №3
«Определение площади смоченной поверхности судна методом трапеций»
Подготовил: ст. гр. СВ-
(Фамилия и инициалы студента)
Проверил: преподаватель
Погодаева А.С.
Севастополь – 2016
Строевые по шпангоутам и ватерлиниям. Метод трапеций.
Для характеристики распределения сил водоизмещения по длине судна строят специальную эпюру, называемую строевой по шпангоутам (рис.3). Для построения этой эпюры горизонтальная линия, выраженная в принятом масштабе теоретическую длину судна, делится на n одинаковых частей, равных числу шпаций на теоретическом чертеже судна.
Рис. 3.1 - Строевая по шпангоутам
На перпендикулярах, восстановленных в точках деления, откладывают в определенном масштабе величины площадей погруженных частей соответствующих шпангоутов, и концы этих отрезков соединяют плавной линией. Площадь строевой по шпангоутам равна объему водоизмещения судна.
Так как ЦВ судна находится в ЦТ подводной части судна, а площадь строевой выражает собой объем подводной части, то абсцисса ЦТ строевой по шпангоутам равна абсциссе ЦВ судна.
Аналогичная эпюра, характеризующая распределение сил водоизмещения по высоте судна, называется строевой по ватерлинии (рис.4).
Рис. 3.2 – Строевая по ватерлиниям
Площадь строевой по ватерлиниям также равна объемному водоизмещению судна, а ордината ее центра тяжести определяет положение центра величины судна по его высоте.
Если учесть свойства строевых по шпангоутам и ватерлиниям, то определение местоположения центра величины судна сведется к вычислению абсциссы центра тяжести строевой по шпангоутам и ординаты центра тяжести строевой по ватерлиниям.
Воспользовавшись известным из статики определением для статического момента площади, можно написать формулы для определения координат ЦВ судна:
, 
,
где 
- площади частей строевых, заключенных между двумя смежными шпангоутами или ватерлиниями; 
, 
, 
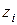- координаты ЦТ соответствующих площадей.
При ориентировочных расчетах можно воспользоваться приближенными формулами для определения местоположения ЦТ, ЦВ и метацентра по высоте судна.
Ордината ЦТ судна определяется по выражению:
,
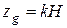где k - практический коэффициент, значение которого, например, для катеров лежит в пределах 0,68 - 0,73; 
- высота борта судна.
Для вычисления ординаты ЦВ рекомендуется формула академика В.Л. Поздюнина:
,
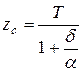где Т – осадка судна; 
- коэффициент полноты водоизмещения;
- коэффициент полноты ГВЛ.
При вычислении координат ЦT судна используется известная из теоретической механики теорема о статическом моменте равнодействующей силы: если данные силы приводятся к одной равнодействующей, то момент равнодействующей относительно какой-либо оси (плоскости) равен сумме моментов составляющих сил относительно той же оси (плоскости).
Применительно к судну на основании этой теоремы можно написать уравнения статических моментов относительно основных координатных плоскостей.
Относительно пл-ти XOZ (ДП): 
Относительно пл-ти УОZ (
): 
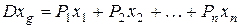
Относительно плоскости XОY (ОП): 
Учитывая, что масса судна 
, из приведенных уравнений получим расчетные формулы для определения координат ЦТ судна:
;
;
,
где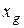 
, 
, 
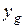- координаты ЦТ судна; P1, P2,... Pn - массы элементов самого судна и перевозимых на нем грузов; 
, 
, 
- координаты ЦТ элементов самого судна и перевозимых грузов.
При использовании этих формул координаты ЦТ элементов самого судна и перевозимых на нем грузов берутся с положительным или отрицательным знаком, в зависимости от положения этих точек по отношению к выбранным координатным плоскостям. Поскольку подводный объем судна симметричен относительно ДП (
), ордината центра тяжести 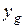также должна быть равна нулю. В противном случае условия равновесия судна не будут удовлетворены, и судно будет плавать с креном.
Для вычисления координат ЦТ судна, с помощью приведенных выше уравнении необходимо просуммировать массы всех элементов судна и находящихся на нем грузов, входящих в состав водоизмещения судна. Вычисление координат ЦТ судна принято производить с помощью таблицы нагрузки масс.
Запас плавучести – это объем надводной водонепроницаемой части корпуса судна или то дополнительное кол-во грузов или воды (после допустимой нагрузки), которое судно может принять до утраты способности держаться на плаву.
Запас плавучести судна можно определить по следующей формуле:
,
где 
– запас плавучести; 
– площадь грузовой ватерлинии;
Н – высота борта; T – осадка судна; k – эмпирический коэффициент, учитывающий развал бортов, седловатость палубы, наличие водонепроницаемых надстроек и рубок.
Степень непотопляемости судна тем выше, чем выше относительный запас плавучести судна, который определяется как отношение запаса плавучести к расчетному водоизмещению судна.
Запас плавучести выражается в процентах от водоизмещения судна в полном грузу и составляет около 80% на пассажирских, 50% на транспортных, сухогрузных и промысловых, 15-25% на наливных судах.
Запас плавучести непосредственно связан с высотой надводного борта.
Расчёта площади погруженной части судна по правилу трапеции:
Si = (ai + bi) / h, м2
a – i-шпангоут, м
b – (i+1)-шпангоут, м
h – шпация, м
Sобщ = S1 + S2 + … + Sn
