Груз массой m = 4кг,получив в точке А начальную скорость V0, движется в изогнутой трубе АВС, расположенной в вертикальном положении. На участке АВ на груз кроме силы тяжести G действует сила сопротивления R=μV, пропорциональная скорости (где μ – коэффициент пропорциональности). В положении В груз, не изменяя значения своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести и силы трения, действует переменная сила Q.
Зная время движения t=2с на участке АВ и скорость груза в точке В, определить:
1) начальную скорость груза V0, которую имел груз в положении А;
2) закон движения груза на участке АВ х = f(t);
3) длину участка l АВ;
4) закон движения груза на участке ВС х = f(t).
При окончательных расчетах принять коэффициент трения f = 0,2, g = 10 м/с2. Другие необходимые для расчета данные приведены в табл. Д1.
Таблица Д1 Исходные данные для задачи Д1.
| Вариант | ||||||||||||||||||||
| µ | 0,2 | 0,4 | 0,6 | 0,8 | 0,2 | 0,4 | 0,6 | 0,8 | 0,2 | 0,4 | ||||||||||
| VВ (м/с) | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 2,0 | 2,5 | 3,0 | 4,0 | 2,0 | ||||||||||
| Q (H) | -sin2t | 6t2-1 | cos2t | 1-2t | 2t2 | e-2t | -cos2t | 2sin3t | e2t | sin2t | ||||||||||

Рисунок D1
Решение
1. Считая груз материальной точкой, рассмотрим его движение на участке АВ. На груз действует сила тяжести G, сила сопротивления R и нормальная реакция N. Проводим координатные оси ху и составляем дифференциальное уравнение движения груза в проекции на ось х:
 . (1)
. (1)
Учитывая, что  , а R=µV, получим
, а R=µV, получим


 Разделяя переменные V и t и принимая g=10 м/с2,получим
Разделяя переменные V и t и принимая g=10 м/с2,получим
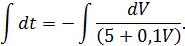
Введем новую переменную
 , тогда
, тогда  ; откуда
; откуда  .
.
Следовательно:

Постоянную C1 находим из (2) при начальных условиях (t =0, V = V0:



 Когда через время τ = 2 с груз переместится в точку В, скорость его равна:
Когда через время τ = 2 с груз переместится в точку В, скорость его равна:
 2. Начальную скорость V0, сообщенную грузу в точке А, определяем из уравнения (5) при VB = 2 м/с и τ = 2 с:
2. Начальную скорость V0, сообщенную грузу в точке А, определяем из уравнения (5) при VB = 2 м/с и τ = 2 с:
 (6)
(6)
3. Определяем длину участка АВ. Для этого сначала найдем уравнение движения груза на этом участке, подставляя в уравнение (3) V=dx/dt. Разделяя переменные х и t, получим
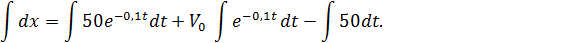 В результате интегрирования
В результате интегрирования
 Постоянную С2 находим из уравнения (7) при начальных условиях (t = 0, х = х0 = 0):
Постоянную С2 находим из уравнения (7) при начальных условиях (t = 0, х = х0 = 0):
 Тогда уравнение движения груза на участке АВ будет иметь вид
Тогда уравнение движения груза на участке АВ будет иметь вид
 Длина участка АВ при τ =2с равна:
Длина участка АВ при τ =2с равна:
 (9)
(9)
4. Рассмотрим движение груза на участке ВС. Скорость VВ = 2 м/с на этом участке будет начальной. Изображаем груз в произвольном положении и действующие на него силы Fx, G, F тp, а также нормальную реакцию плоскости N. Составляем дифференциальное уравнение движения груза на этом участке в проекции на ось х:


где сила трения  .
.
Для определения нормальной реакции плоскости N составим уравнение равновесия сил в проекции на ось у:
 ;
;  , откуда
, откуда 
Следовательно: 
 Откуда, разделив на массу, получим
Откуда, разделив на массу, получим
 .
.
После интегрирования:

Заменив 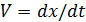 , имеем
, имеем
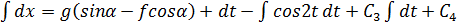 .
.
После повторного интегрирования:

Постоянные С3 и С4 находим из уравнений (8) и (9) при начальных условиях (t = 0, х0 = 0, V0 = VB):
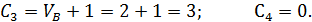
Тогда закон движения груза на участке ВС будет иметь вид

Ответ:

6.8. Задача Д2. Применение основных теорем динамики к исследованию движения материальной точки
Груз массой m, получив начальную скорость в точке А, движется внутри полой трубки, расположенной в вертикальной плоскости под действием силы тяжести G и силы трения F тр. Зная скорость груза в точке В и время движения τ на участке АВ, а также величину коэффициента трения f на этом участке трубки, определить:
1) скорость груза в точках А, C и D;
2) силу давления груза на стенку трубки в точке С.
При окончательных расчетах принять f = 0,2; m = 2 кг; R = 6 м; g =10 м/с2. Другие необходимые для решения данные приведены в табл. Д2.
Таблица Д2 Исходные данные для задачи Д2.
| Вариант | ||||||||||
| τ (с) | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| VВ (м/с) |

Пример Д2. Дано: VB =1 м/с; m = 2 кг; α = 300; τ = 0,7 с; R = 6 м; f = 0,2. Определить: скорость груза в положениях А,С и D и силу давления груза на стенку трубки в положении С.
Решение
| Рисунок Д2 |
2. Для определения начальной скорости груза в точке А применим теорему об изменении количества движения материальной точки:
 .
.
Для нашего случая:

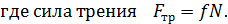
Нормальную реакцию определяем, проецируя силы на ось y:

Следовательно: 
Из уравнения (1) скорость груза в точке A равна:
 .
.
3. Определяем скорость груза в точке С, применяя теорему об изменении кинетической энергии для материальной точки:
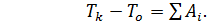
Для нашего случая:
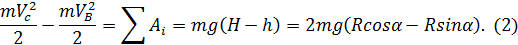 Откуда скорость груза в точке С:
Откуда скорость груза в точке С:
 .
.
4. Определяем силу давления N груза на стенку трубки в точке С, применяя принцип Даламбера для материальной точки:
 (3)
(3)
Составляем сумму проекций этих сил на нормаль:
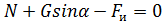 (4)
(4)
и определяем силу инерции, условно приложенную к грузу:
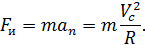
Откуда реакция стенки трубки равна


А сила давления груза на стенку трубки в точке С, по закону равенства действия и противодействия, равна реакции стенки:

5. Определяем скорость груза в точке D, применяя теорему об изменении кинетической энергии для материальной точки:

Откуда скорость груза в точке D равна:
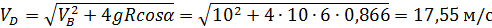 .
.
Ответ:

ЛИТЕРАТУРА
Основная
1. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики: Учебник. Т.1.: Статика. Кинематика. - М.: Наука, 1985.- 240 с.
2. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики: Учебник. Т. 2.: Динамика. - М.: Наука, 1985.- 496 с.
3. Гернет М.М. Курс теоретической механики.– М.: Высш. шк., 1981. -303 с.
4. Тарг С.М. Краткий курс теоретической механики: Учебник. -М.: Высш. шк., 2002. - 416 с.
5. Яблонский А.А., Никифорова В.М. Курс теоретической механики. Статика. Кинематика. Динамика: Учебник.– СПб.:Издательство «Лань», 2001. - 768 с.
Дополнительная
1. Айзенберг Т.Б., Воронков Н.М., Осецкий В.М. Руководство к решению задач по теоретической механике./Под редакцией проф. И.М. Воронкова. – М.: Высш. шк., 1968.- 419 с.
| Луганский национальный аграрный университет Кафедра сопротивления материалов и теоретической механики РАСЧЕТНО – ГРАФИЧЕСКАЯ РАБОТА ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ Студента (ки) _____ курс ______ группа Направление подготовки__________________ Специальность_______________________ _ _________________________________ (Фамилия и инициалы) Руководитель___________________________ _______________________ _ ____________ (должность, ученое звание, научная степень,фамилия и инициалы) Национальная шкала ________________ Количество балов: ______ Оценка: ECTS ____ Луганск – 2015 |
ПРИЛОЖЕНИЯ
Образец выполнения титульного листа
Приложение 1
Приложение 2 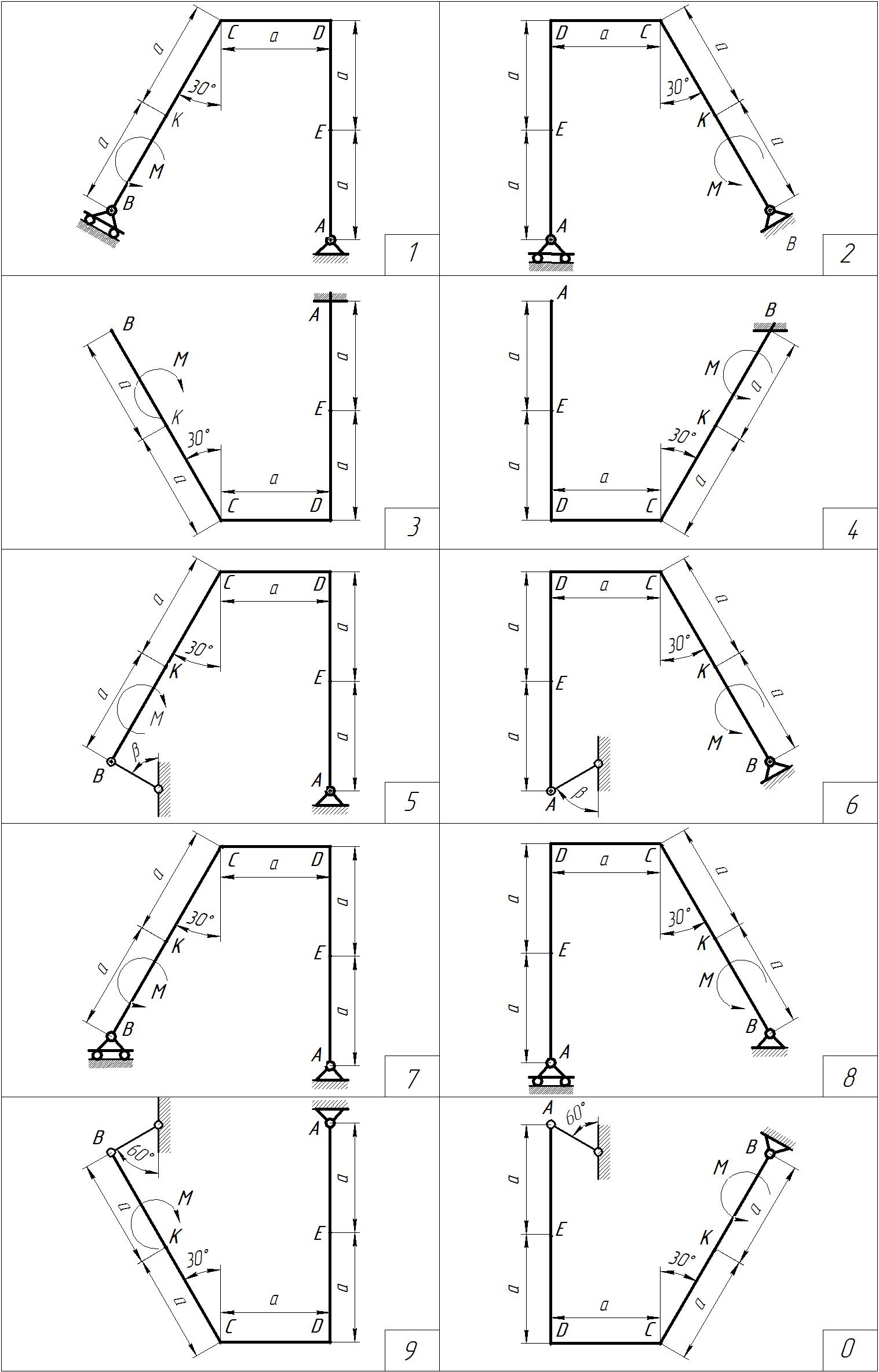
Рисунок С1
Приложение 3
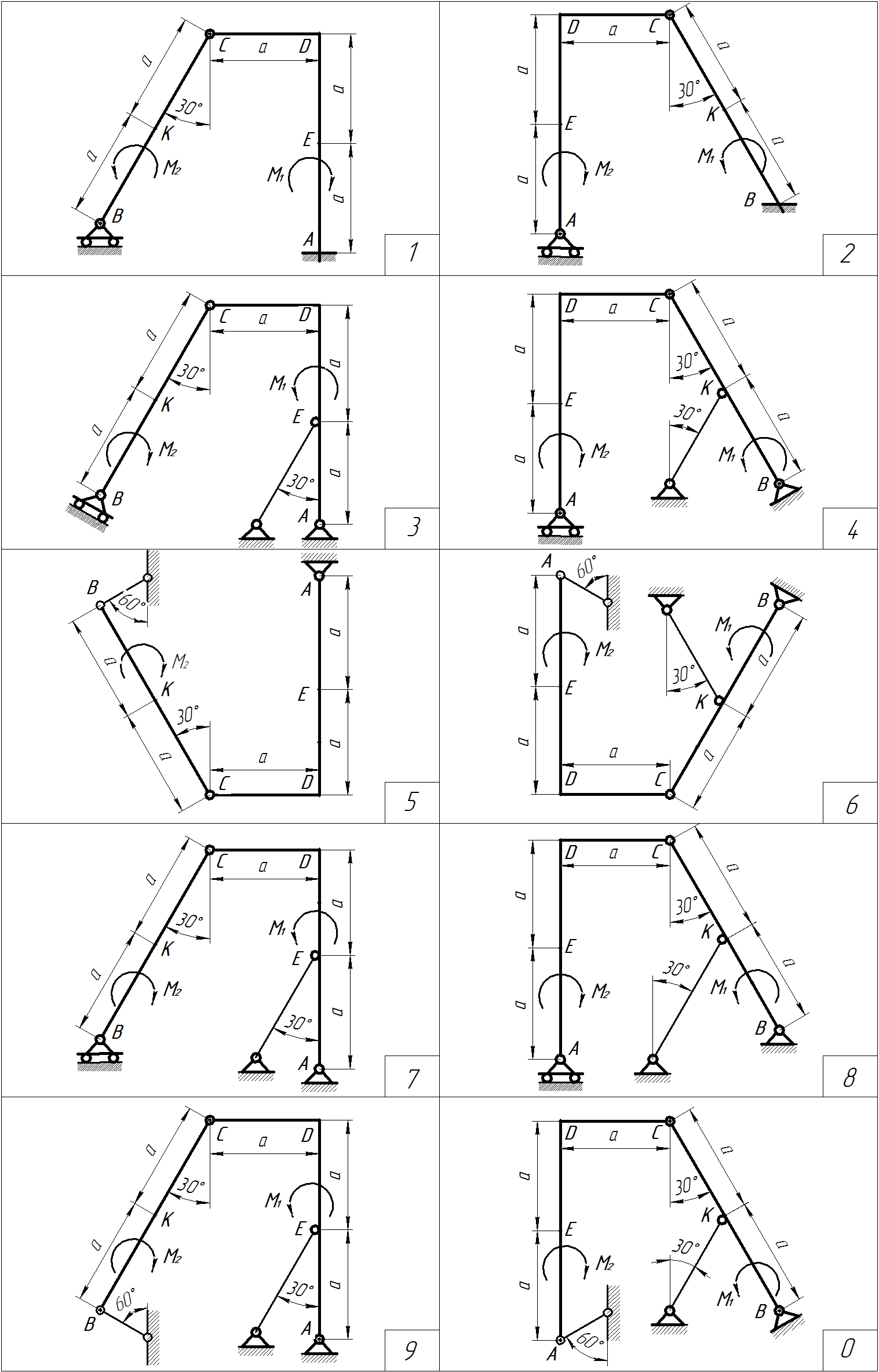
Рисунок С2
Приложение 4

Рисунок С3
Приложение 5

Рисунок С4
Приложение 8

Рисунок Д1
Приложение 9

Рисунок Д2




