На простую плоскую конструкцию могут быть наложены связи:
1) заделка (защемление);
2) неподвижный цилиндрический шарнир;
3) шарнирная опора на катках;
4) прямолинейный невесомый стержень с шарнирами на концах.
На конструкцию действует нагрузка:
1) пара сил с моментом: М = 10 Нм;
2) сосредоточенные силы: F1 = 10 Н, F2 = 20 Н, F3 = 30 Н, F4 = 40 Н.
Определить реакции связей в точках А и В, вызываемые действующими нагрузками, и сделать проверку полученных результатов, составив уравнение моментов относительно точки D. При окончательных расчетах принять:  а = 0,4 м.
а = 0,4 м.
Направление и точки приложения сил указаны в табл. С1.
Таблица С1 Исходные данные для задачи С1.
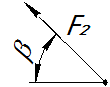
| Силы | 
| 
|
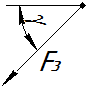
|

| ||||
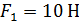
| 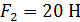
| 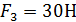
| 
| |||||
| Вариант | Точка прило-жения | α, град. | Точка прило-жения | β, град. | Точка прило-жения | γ, град. | Точка прило-жения | φ, град. |
| Е | - | - | - | - | C | |||
| - | - | E | K | - | - | |||
| C | - | - | - | - | E | |||
| - | - | C | E | - | - | |||
| K | - | - | - | - | D | |||
| - | - | K | D | - | - | |||
| D | - | - | - | - | K | |||
| - | - | D | K | - | - | |||
| E | - | - | - | - | C | |||
| - | - | Е | C | - | - |
Пример С1. Дано: α = 300; β=600; F1 = 10 Н; F2 = 20 Н; М = 10 Нм;
а = 0,4 м. Определить реакции связей RA и MA, вызванные заданной нагрузкой. (рис. С1).
 Решение
Решение
1. Проводим координатные оси xy и изображаем действующую на конструкцию нагрузку: силы F1, F 2 и пару сил с моментом М.
2. Изображаем реакции связей, действующие в жесткой заделке (точка А):  ,
, 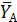
и реактивный момент МА.
| Рисунок С1 |
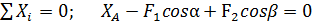 ; (1)
; (1)
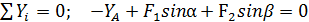 ; (2)
; (2)
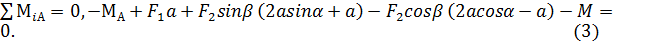 .
.
Реакцию ХА определяем из уравнения (1):
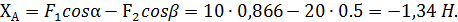
Реакцию YА определяем из уравнения (2):
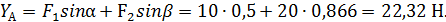
Реактивный момент МА определяем из уравнения (3):
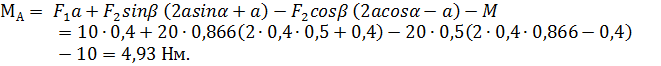
Модуль реакции определяем по формуле

Проверка. Для проверки результатов составляем сумму моментов относительно точки D:
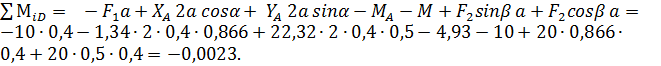
Полученное значение соответствует точности проведенных вычислений и подтверждает достоверность полученных результатов.
Ответ: 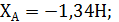
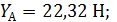
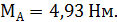
Задача С2. Определение реакций связей составной конструкции
На плоскую конструкцию, состоящую из двух частей и соединенных в точке С шарниром, могут быть наложены связи:
1) заделка (защемление);
2) неподвижный цилиндрический шарнир;
3) шарнирная опора на катках.
На конструкцию действует нагрузка:
1) пара сил с моментом: М = 10 Нм;
2) сосредоточенные силы: F1 = 10 Н, F2 = 20 Н, F3 = 30 Н, F4 = 40 Н.
Определить реакции связей в точках А, В и С, вызываемые действующими нагрузками и сделать проверку полученных результатов, составив уравнение моментов относительно точки D. При окончательных расчетах принять:  а = 0,4 м.
а = 0,4 м.
Направление и точки приложения сил указаны в табл. С2.
Таблица С2Исходные данные для задачи С2.
| Силы | 
| 
|

|

| ||||
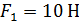
| 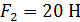
| 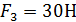
| 
| |||||
| Вариант | Точка прило-жения | α, град. | Точка прило-жения | β, град. | Точка прило-жения | γ, град. | Точка прило-жения | φ, град. |
| Е | - | - | - | - | К | |||
| - | - | E | K | - | - | |||
| K | - | - | - | - | D | |||
| - | - | К | D | - | - | |||
| D | - | - | - | - | К | |||
| - | D | K | - | - | ||||
| Е | - | - | - | - | K | |||
| - | - | E | K | - | - | |||
| К | - | - | - | - | D | |||
| - | - | K | D | - | - |
Пример С2. Дано: α = 300; β = 600; F1 = 10 Н; F2 = 20 Н; М = 10 Нм; а = 0,4 м. Определить реакции связей RA RB и RC, вызванные заданными нагрузками (рис. С2).

Рисунок С2
Решение
1. Для определения реакций расчленим конструкцию (рис. С2, а) на две части и рассмотрим сначала равновесии стержня ВС. Проводим координатные оси xy и изображаем действующую на стержень нагрузку: силу F2 и момент М. Изображаем реакции связей. Направление реакции связи RB в точке В известно, а в точке С неизвестно. Поэтому эту реакцию раскладываем на составляющие по осям координат XC,YC, произвольно выбирая направление.
2. Для произвольной плоской системы сил составляем три уравнения равновесия, предварительно разложив силы на составляющие (рис. С2,б):
 ; (1)
; (1)
 ; (2)
; (2)
 . (3)
. (3)
Реакцию ХС определяем из уравнения (3):

Реакцию RB определяем из уравнения (1):
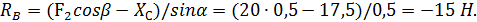
Реакцию  определяем из уравнения (2):
определяем из уравнения (2):
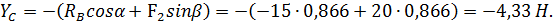
2. Для определения реакций в точке А рассмотрим равновесие угольника ADC, изображая нагрузку (силу F2) и реакции связей RA и МА, произвольно выбирая их направление. Составляем уравнения равновесия сил и моментов для угольника ADC. (рис. С2, в):
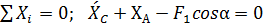 ; (4)
; (4)
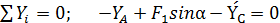 ; (5)
; (5)
 (6)
(6)
Реакцию ХА определяем из уравнения (4):
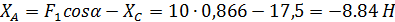 .
.
Реакцию 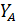 определяем из уравнения (5):
определяем из уравнения (5):
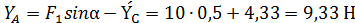 .
.
Реактивный момент определяем из уравнения (6):


Модули реакций определяем по формулам:


Проверка. Составляем уравнение моментов относительно точки D для всей конструкции (рис.2 a):

Полученное значение соответствует точности проведенных вычислений и подтверждает достоверность полученных результатов.
Ответ: 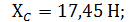
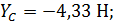
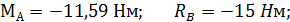
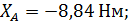
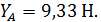
Знак (-) показывает, что реакция направлена в обратную сторону.






