ЗНАНИЯ И УМЕНИЯ, НЕОБХОДИМЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧ
Разложение силы на составляющие по осям координат
Чтобы разложить силу F на составляющие (Fx и Fy)по осям координат, необходимо через точку приложения А силы провести прямые, параллельные осям координат (x и y), и на эти прямые опустить перпендикуляры из конца (рис.1, a)или начала вектора силы F (рис.1, б).
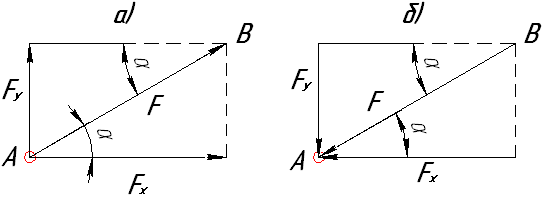
Рисунок 1
Проекция силы на ось
Проекция силы на ось - это скалярная величина, равная произведению модуля силы на косинус угла α между вектором силы и положительным направлением оси (рис. 2). Обозначим α угол, образованный вектором силы с положительным направлением оси. Тогда получим
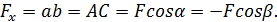 Если этот угол острый - проекция положительна, если тупой – отрицательна. Проекция силы на ось равна нулю, если сила перпендикулярна оси (рис.2 в).
Если этот угол острый - проекция положительна, если тупой – отрицательна. Проекция силы на ось равна нулю, если сила перпендикулярна оси (рис.2 в).
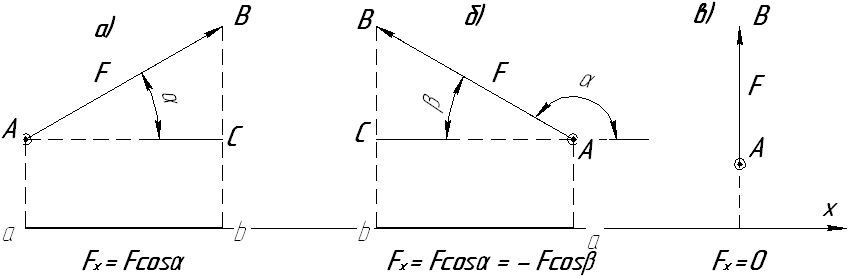
Рисунок 2
Момент силы относительно точки
Момент силы относительно точки (центра) это векторная величина численно равная произведению модуля силы на ее плечо:
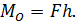
Плечо силы - это длина перпендикуляра, опущенного из центра момента (точка О) на линию действия силы (рис.3).
Линия действия силы -это прямая, по которой направлена сила.
Если сила 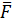 стремится вращать плоскость ее действия вокруг данной точки О против часовой стрелки (рис.3 а), то момент силы относительно этой точки считается положительным, в противном случае – отрицательным (рис.3 б). Если линия действия силы
стремится вращать плоскость ее действия вокруг данной точки О против часовой стрелки (рис.3 а), то момент силы относительно этой точки считается положительным, в противном случае – отрицательным (рис.3 б). Если линия действия силы 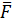 проходит через центр момента (точку О) (рис.3 в), то момент силы относительно этой точки равен нулю.
проходит через центр момента (точку О) (рис.3 в), то момент силы относительно этой точки равен нулю.
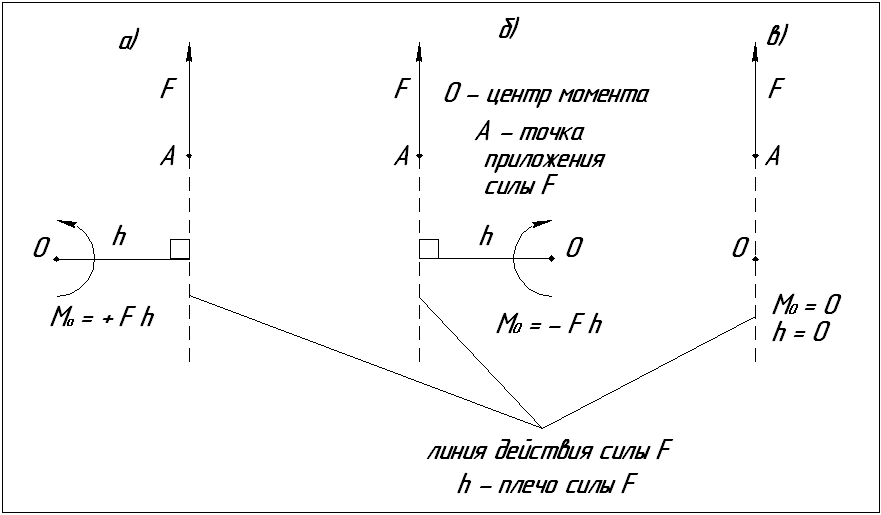
Рисунок 3
Момент силы относительно оси
Момент силы относительно оси – это скалярная величина, которая численно равна моменту проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью (точка О):
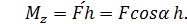
Таким образом, для определения момента силы относительно любой оси (например оси z, рис. 4,а), следует спроецировать силу 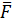 на плоскость Q, перпендикулярную данной оси и определить момент полученной проекции
на плоскость Q, перпендикулярную данной оси и определить момент полученной проекции 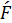 относительно точки пересечения О оси с плоскостью Q.
относительно точки пересечения О оси с плоскостью Q.
Момент силы относительно оси считается положительным, если при наблюдении с положительного направления оси видно, что проекция 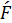 стремится вращать плоскость ее действия против хода часовой стрелки (рис. 4 а), в противном случае – отрицательным.
стремится вращать плоскость ее действия против хода часовой стрелки (рис. 4 а), в противном случае – отрицательным.
Момент силы относительно оси равен нулю в двух случаях (рис. 4б):
1) если сила 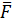 параллельна оси (проекция
параллельна оси (проекция 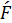 равна нулю);
равна нулю);
2) линия действия силы пересекает ось (плечо h проекции силы равно нулю).
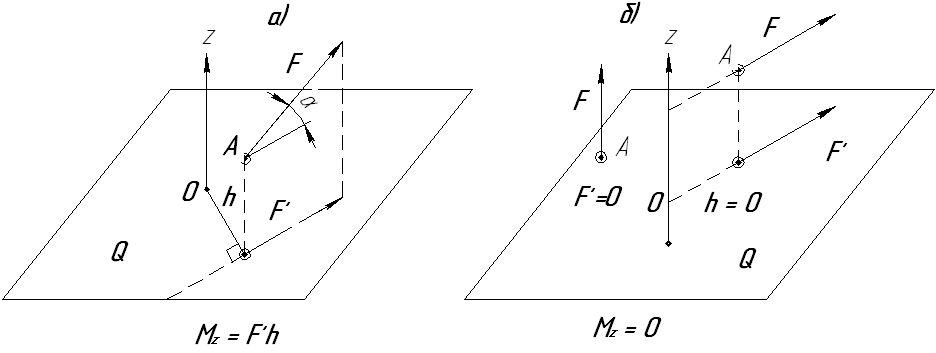
Рисунок 4
Пара сил и ее момент
Пара сил – это система двух равных по модулю, параллельных и противоположных по направлению сил (рис. 5).
Основными характеристиками пары сил являются:
1) плоскость действия пары сил – это плоскость, в которой находятся линии действия пары сил (на рис. 5 – это плоскость Q);
2) плечо пары (d) – это кратчайшее расстояние между линиями действия пары сил. Для определения плеча пары необходимо из любой точки линии действия одной силы пары опустить перпендикуляр на линию действия другой силы.
Момент пары сил - это векторная величина, численно равная произведению модуля одной силы на расстояние между линиями действия этих сил:
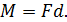
При этом момент считается положительным, когда пара сил стремится вращать плоскость ее действия против хода часовой стрелки (рис. 5, а), в противном случае – отрицательным (рис. 5,б).
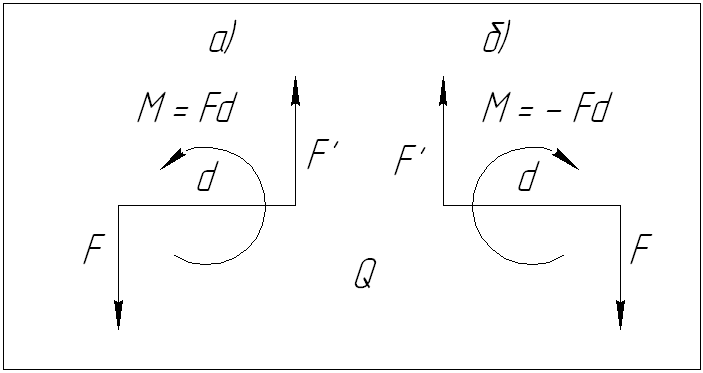
Рисунок 5
Связи. Реакции связей
Связь – это ограничение, налагаемое на движение материального объекта в пространстве.
Например, движение книги, лежащей на столе, ограничено поверхностью стола. Поверхность стола для книги является связью.
Реакция связи – это сила или система сил, с которой связь действует на рассматриваемый объект.
Величина реакции связи и ее направление зависит от сил, действующих на материальный объект, на который наложена данная связь, поэтому реакции связей называют пассивными силами.
Основные типы связей без трения, наложенных на некоторое тело, и их реакции приведены в табл.1. Если проанализировать данные табл.1, то можно сформулировать следующее правило:
Реакция связи направлена в сторону, противоположную тому направлению, по которому связь препятствует двигаться телу. Данное правило облегчает определение направлений реакций связей. Оно также дает возможность определить направление реакций других, не приведенных в табл.1, связей.
Таблица1 Схемы реакций связей
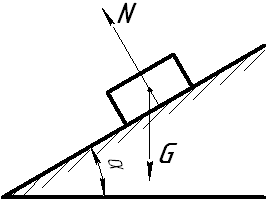 реакция идеально гладкой поверхности реакция идеально гладкой поверхности
| 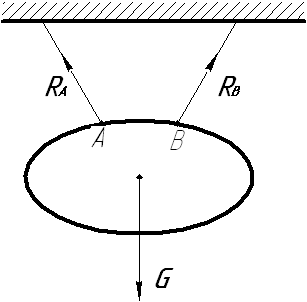 реакция гибкого тела (нить,трос, канат, цепь) реакция гибкого тела (нить,трос, канат, цепь)
|
реакция шарнирно-подвижной опоры 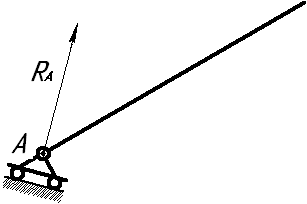
| 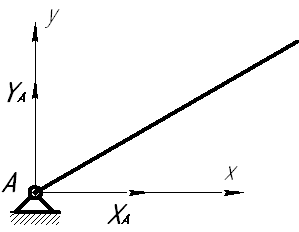 реакция шарнирно-неподвижной опоры реакция шарнирно-неподвижной опоры
|
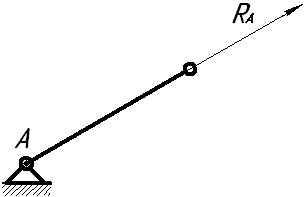 реакция невесомого стержня с шарнирами на концах реакция невесомого стержня с шарнирами на концах
| 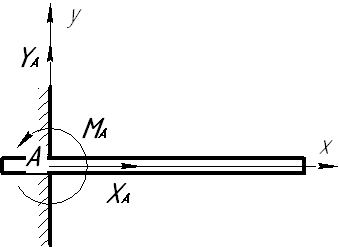 реакция в заделке (балка жестко заделана в стену) реакция в заделке (балка жестко заделана в стену)
|
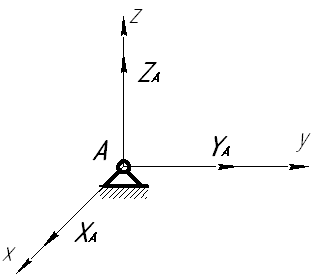 реакция сферического шарнира реакция сферического шарнира
| 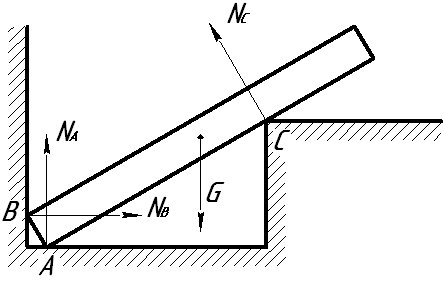 реакция идеально гладкой поверхности и точечной опоры реакция идеально гладкой поверхности и точечной опоры
|
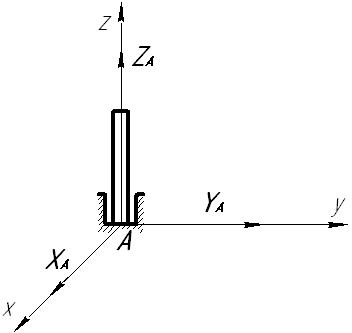 реакция подпятника (упорного подшипника) реакция подпятника (упорного подшипника)
| 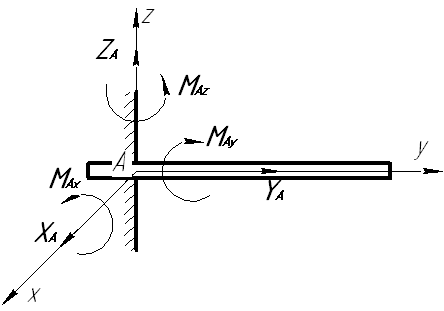 реакция пространственной заделки реакция пространственной заделки
|
5. ОБЩИЕ ПОЛОЖЕНИЯ И ПРАВИЛА ОФОРМЛЕНИЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ
5.1. Цель и задачи расчетно-графической работы.
Основной целью расчетно-графической работы является закрепление, углубление и обобщение теоретических знаний, полученных студентами при изучении курса, развитие навыков при решении практических задач.
5.2. Выбор вариантов контрольных заданий.
Выбор вариантов осуществляется по шифру (две последние цифры зачетной книжки): вариант рисунка - по первой цифре шифра, а условие в таблице – по второй цифре. Например, при двух последних цифрах зачетной книжки 49: вариант рисунка – 4, условие к задачам – 9. Рисунки к задачам приведены в приложениях в конце методических указаний.
5.3. Требования к оформлению расчетно-графической работы
Расчетно-графическая работа выполняется на листах формата А4. Титульный лист контрольного задания оформляется согласно приложению 12. Решение каждой задачи необходимо начинать с новой страницы.
Рисунки к решениям задач должны быть выполнены в масштабе, с применением чертежных принадлежностей. На рисунке должны быть приведены обозначения всех используемых в решении величин, размеры, координатные оси, векторы сил, скоростей, ускорений и т.д. Обязательно должны быть указаны единицы измерения физических величин в системе СИ.
Решение задач должно сопровождаться краткими текстовыми пояснениями (какие формулы или теоремы применяются, как получаются те или иные результаты и т.п.) и подробным изложением всех выполняемых расчетов. Текст работы выполняется чернилами синего или черного цвета на листах формата А4. Разрешается выполнять текст путем компьютерного набора. При компьютерном наборе рекомендуется использовать шрифт Times New Roman, размер - 14 пунктов, межстрочный интервал – одинарный. Все листы нумеруются.
Условные буквенные обозначения (символы) физических, математических и других величин должны соответствовать установленным стандартам.
Математические формулы должны быть расположены отдельными строками. Обозначение единицы физической величины в математическую формулу следует помещать только после конечного результата вычисления.
Работы, не отвечающие вышеперечисленным требованиям, возвращаются студенту для исправления. Все исправления по замечаниям рецензента должны быть выполнены в конце той же работы с соответствующими ссылками - что исправляется и в какой задаче. При полном переоформлении работы или выполнении исправлений в отдельной работе первоначальное решение должно обязательно прилагаться.
Расчетно-графическая работа должна быть зачтена до начала экзаменационной сессии.
ЗАДАНИЯ ДЛЯ РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ И ПРИМЕРЫ ИХ ВЫПОЛНЕНИЯ
(Исходные данные к задачам приведены в таблицах, а рисунки в приложениях в конце методических указаний).






