Лекция 8. Данные, их типы, структуры и обработка

Рассматриваются основные понятия о данных к алгоритмам, их базовые типы и структуры, вопросы их использования в алгоритмизации задач.

Любая актуализация информации опирается на какие-то данные, любые данные могут быть каким-то образом актуализированы.

Данные – это некоторые сообщения, слова в некотором заданном алфавите.

Пример. Число 123 – данное, представляющее собой слово в алфавите из десяти натуральных цифр; число 12,34 – данное, представляющее собой слово в алфавите из десяти натуральных цифр и десятичной запятой; текст "математика и информатика – нужные дисциплины", – данное в алфавите из символов русского языка и знаков препинания, включая пробел.

Текущее (то есть рассматриваемое в данный момент времени) состояние данных называют текущим значением данных или просто значением.

Тип данных характеризует область определения значений данных.

Задаются типы данных простым перечислением значений типа, например как в простых типах данных, либо объединением (структурированием) ранее определенных каких-то типов – структурированные типы данных.

Пример. Зададим простые типы данных "специальность", "студент", "вуз" следующим перечислением:

специальность = (филолог, историк, математик, медик);

студент = (Петров, Николаев, Семенов, Иванова, Петрова);

вуз = (МГУ, РГУ, КБГУ).

Значением типа "студент" может быть Петров.

Пример. Опишем структурированный тип данных "специальность_студента":

специальность_студента=(специальность, студент).

Значением типа "специальность_студента" может быть пара (историк, Семенов).

Для обозначения текущих значений данных используются константы – числовые, текстовые, логические.

Часто (в зависимости от задачи) рассматривают данные, которые имеют не только "линейную" (как приведенные выше), но и иерархическую структуру.

Пример. Структуру "вуз" можно задать иерархической структурой, состоящей, например, из следующих уровней: "Ректорат", "Деканаты и подразделения", "Кафедры", "Отделы", "Преподаватели и сотрудники".

В алгоритмических языках есть стандартные типы, например, целые, вещественные, символьные, текстовые и логические типы. Они в этих языках не уточняются (не определяются, описываются явно) и имеют соответствующие описания с помощью служебных слов.

Пример. В школьном алгоритмическом языке (ШАЯ), например, целые, вещественные, символьные, текстовые (литерные, стринговые) и логические типы данных описываются ключевыми словами цел, вещ, сим, лит, лог. В языке Паскаль – аналогичными ключевыми словами integer, real, char, string, boolean.

Каждый тип данных допускает использование определенных операций со значениями типа ("с типом").

Пример. Для целого типа данных назовем операции ":=", "+", "–", "*", "=" (сравнение на равенство), " ", "<", ">", " ", " "..

Для вещественного типа данных еще и операция "/" (деление).

Для символьного типа данных – только ":=", "=", " ", "<", ">", " ", " ". Например, сравнение "а"<"b" означает, что символ "а" предшествует символу "b" то есть код буквы "a" меньше кода буквы "b" (коды символов приводятся, например, в таблице ASCII – Аmerican Standard Code for Information Interchange, американский стандарт кодирования для обмена данными).

Для текстового (литерного) типа данных можно использовать еще и операцию конкатенации (присоединения справа) текстов "+". Например, "аб"+"ба" даст новый текст "абба".

Для данных логического типа определены логические операции и отношения сравнения. Например, на Паскале для логических переменных a, b, c можно записать корректное выражение: a and b or (c not a).

Для описания переменных, значениями которых могут быть лишь символы, тексты, используются соответствующие ключевые слова: на ШАЯ – сим, лит, на Паскале – char, string.

Текстовые (символьные) константы обычно заключают в апострофы.

Пример. Составим алгоритм подсчета числа несовпадающих символов (на одинаковых позициях текстов) в двух заданных текстах a и b. Метод решения: "вырезаем" и сравниваем символы на одинаковых позициях в текстах на совпадение.

Program EquSimb;Uses Crt;Var i, k, j: integer; a, b: string;Begin ClrScr; WriteLn('Введите строку a = '); { приглашение к вводу входного параметра } ReadLn(a); { ввод первого входного параметра } WriteLn('Введите строку b='); { приглашение к вводу второго параметра } ReadLn(b); { ввод второго входного параметра } k:=abs(length(a)–length(b)); { вычисление разницы длин текстов } if (length(a)<length(b)) { если текст b длиннее текста a,} then j:=length(a) { то проверять нужно до длины a, } else j:=length(b); { иначе – до длины b } for i:=1 to j do { цикл проверки на совпадение символов } if (a[i]<>b[i]) { если символы тестов на одинаковых позициях не равны, } then k:=k+1; { то увеличиваем счетчик количества таких символов } WriteLn('k = ',k); { вывод результата }End.

Наиболее часто используемая структура данных – массив.

Одномерный массив (вектор, ряд, линейная таблица) – это совокупность значений некоторого простого типа (целого, вещественного, символьного, текстового или логического типа), перенумерованных в каком-то порядке и имеющих общее имя. Для выделения конкретного элемента массива необходимо указать его порядковый номер в этом ряду.

Пример. Последовательность чисел 89, –65, 9, 0, –1.7 может образовывать одномерный вещественный массив размерности 5, например, с именем x вида: x[1] = 89, x[2] = –65, x[3] = 9, x[4] = 0, x[5] = –1.7.

Значение порядкового номера элемента массива называется индексом элемента.

Пример. Можно ссылаться на элемент х[4], элемент х[i], элемент x[4+j] массива х. При текущих значениях переменных i = 2 и j = 1 эти индексы определяют, соответственно, 4-й, 2-й и 5-й элементы массива.

Для обозначения (нового типа объектов) массивов в алгоритмических языках обычно вводится специальное служебное слово.

Пример. На Паскале имеется соответствующее слово array. На Паскале (в рамках рассматриваемого нами его ядра) необходимо указывать предельную величину размерности:

x: array [1..100] of real;.

Двумерный массив (матрица, прямоугольная таблица) – совокупность одномерных векторов, рассматриваемых либо "горизонтально" (векторов-строк), либо "вертикально" (векторов-столбцов) и имеющих одинаковую размерность, одинаковый тип и общее имя.

Матрицы, как и векторы, должны быть в алгоритме описаны служебным словом (например, таб или array), но в отличие от вектора, матрица имеет описание двух индексов, разделяемых запятыми: первый определяет начальное и конечное значение номеров строк, а второй – столбцов.

Пример. Если матрица x описана в виде

x: array [1..5, 1..3] of real;,

то определяется таблица из 5 строк (от 1-й до 5-й строки) и 3 столбцов (от 1-го до 3-го столбца) вида:

(столбец 1)	(столбец 2)	(столбец 3)
x₁₁	x₁₂	х₁₃	(строка 1)
x₂₁	x₂₂	х₂₃	(строка 2)
х₃₁	х₃₂	х₃₃	(строка 3)
х₄₁	x₄₂	х₄₃	(строка 4)
х₅₁	x₅₂	х₅₃	(строка 5)

Для актуализации элемента двумерного массива нужны два его индекса – номер строки и номер столбца, на пересечении которых стоит этот элемент.

Пример. Элемент х[3,2] – элемент на пересечении 3-й строки и 2-го столбца массива х.

Рассмотрим ряд задач, решаемых с помощью массивов.

Пример. Составим алгоритм (программу) нахождения суммы и произведения всех элементов одномерного массива. Метод решения: начиная с нулевого значения суммы, добавляем поочередно новый элемент ряда и находим значение искомой суммы; начиная с начального, единичного произведения, находим искомое произведение, умножая текущее значение произведения на очередной элемент ряда. Алгоритм (программа) имеет вид

Program SPM1;Uses Crt;Var x: array [1..100] of real; n, i: integer; s, р: real;Begin ClrScr; WriteLn('Введите размерность массива:'); { приглашение к вводу входного параметра } ReadLn(n); { ввод входного параметра } WriteLn('Введите элементы массива:'); { приглашение к вводу массива } for i:=1 to n do { цикл ввода элементов массива } begin write('x[',i,']='); { приглашение к вводу текущего элемента массива} readln(x[i]) { ввод текущего элемента массива } end; s:=0; { начальное значение суммы – нуль } p:=1; { начальное значение произведение – единица [u1]} for i:=1 to n do { цикл вычисления суммы и произведения } begin s:=s+x[i]; { добавление к сумме очередного слагаемого } p:=p*x[i] { домножение произведения на очередной множитель } end; WriteLn('Полученная сумма равна ', s: 3:3); { вывод полученной суммы } WriteLn('Полученное произведение равно ', p: 3:3); { вывод полученного произведения }End.

Пример. Составим алгоритм вычисления суммы бесконечного ряда чисел а[1], а[2], а[3],... с точностью е, при условии, что точность всегда достигается для номера члена ряда не более 1000000 (это "неестественное" ограничение нужно для того, чтобы в Паскале было проще объявить размерность массива а). Метод решения: сравниваем две суммы – одна сумма была получена на предыдущем шаге суммирования, а вторая – добавлением к ней очередного слагаемого (то есть их разность и равна очередному добавленному элементу ряда); процесс суммирования продолжается до тех пор, пока разность по модулю не станет меньше точности суммирования. Алгоритм (программа) имеет вид

Program SumND;Uses Crt;Var a: array [1..1000000] of real; i: integer; e, p, s: real;begin ClrScr; WriteLn('Введите точность:'); { приглашение к вводу входного параметра } ReadLn(e); { ввод входного параметра } i:=1; { начальный номер члена ряда } WriteLn(‘введите первые два элемента:’); { приглашение к вводу входных параметров } ReadLn(a[1], a[2]); { ввод входных параметров } р:=а[1]; { запоминаем начальную сумму – сумму одного элемента } s:=р+a[2]; { запоминаем начальную следующую сумму – сумму двух элементов } while (abs(s–p)>e) do { цикл суммирования, пока слагаемые влияют на сумму } begin i:=i+1; { переход к следующему элементу } p:=s; { "старую" сумму заменяем "новой", полученной добавлением еще одного } s:=s+а[i]; { вычисляем "новую" сумму } WriteLn(‘введите a[‘, i, ‘]=’); { приглашение к вводу очередного элемента ряда } ReadLn(a[i]); { ввод очередного элемента ряда } end; WriteLn('Полученная сумма равна ', s: 3:3); { вывод результата }End.

Пример. Составим алгоритм вычисления значения полинома P_n(x) = а₀хⁿ + а₁х^n–1 +... + а_n для заданного значения x. Метод решения – метод (схема) Горнера. Опишем его. Заметим, что:

1) при n = 0, P₀(x) = a₀;

2) при n = 1, P₁(x) = a₀x + a₁ = P₀(x) x + a₁;

3) при n = 2, P₂(х) = a₀x² + a₁x + a₂ = (a₀x + a₁)x + a₂ = P₁(x)x + a₂;

...

n) P_n(x) = a₀xⁿ + a₁x^n–1 +... + a_n–1x + a_n = (a₀x^n–1 + a₁x^n–2 +... + a_n–1)x + a_n = P_n–1(x)x + a_n.

Таким образом, всегда верно рекуррентное соотношение Горнера:

Текущее Р:= Предыдущее Р*x + Текущий коэффициент полинома.

Эту схему реализуем в алгоритме (программе) вида:

Program Gorner;Uses Crt;Var a: array [0..100] of real; n, i: integer; p, x: real;Begin ClrScr; WriteLn('Введите порядок полинома:'); { приглашение к вводу входного параметра } ReadLn(n); { ввод первого входного параметра } WriteLn('Введите число x:'); { приглашение к вводу второго входного параметра } ReadLn(x); { ввод второго входного параметра } for i:=0 to n do { цикл схемы Горнера } begin WriteLn('a[',i,']='); { приглашение к вводу очередного коэффициента полинома} ReadLn(a[i]); { ввод очередного коэффициента полинома } end; p:=a[0]; { начальное (для n=0) значение полинома – см. схему Горнера} for i:=1 to n do { цикл накапливания значения полинома по схеме Горнера } p:=p*x+a[i]; { находим полином текущей степени i используя предыдущий } WriteLn('Полученнoe значение p = ', p:3:3); { вывод результата }End.

Пример. Составим алгоритм вычисления суммы и произведения всех элементов a[i,j], i = 1, 2,..., n; j = 1, 2,..., m заданной матрицы. Метод решения: построчно проходя все элементы массива, добавляем к предыдущему значению суммы новый элемент матрицы и умножаем предыдущее значение произведения на этот же элемент. Алгоритм (программа) имеет вид

Program SPM2;Uses Crt;Var a: array [1..100,1..100] of real; n, m, i, j: integer; s, p: real;Begin ClrScr; WriteLn('Введите количество строк:'); { приглашение к вводу входного параметра } ReadLn(n); { ввод первого входного параметра } WriteLn('Введите количество столбцов:'); { приглашение к вводу второго параметра } ReadLn(m); { ввод второго входного параметра } for i:=1 to n do { цикл ввода – перебора строк } for j:=1 to m do { цикл перебора элементов текущей строки } begin WriteLn('a[',i,',',j,']='); { приглашение к вводу очередного элемента массива } ReadLn(a[i,j]); { ввод очередного элемента массива } end; s:=0; { начальное значение суммы – нуль } p:=1; { начальное значение произведения – единица } for i:=1 to n do { цикл перебора строк для суммирования } for j:=1 to m do { цикл перебора элементов строки (столбцов) для суммирования } begin s:=s+a[i,j]; { добавление очередного элемента к текущему значению суммы} p:=p*a[i,j]; { умножение текущего значения произведения на новый элемент } end; WriteLn('Сумма равно: ', s:3:3); { вывод первого результата } WriteLn('Произведение равно: ', p:3:3); { вывод второго результата }End.

Введение в базы данных

Что такое база данных

Можно с большой степенью достоверности утверждать, что большинство приложений, которые предназначены для выполнения хотя бы какой-нибудь полезной работы, тем или иным образом используют структурированную информацию или, другими словами, упорядоченные данные. Такими данными могут быть, например, списки заказов на тот или иной товар, списки предъявленных и оплаченных счетов или список телефонных номеров ваших знакомых. Обычное расписание движения автобусов в вашем городе - это тоже пример упорядоченных данных.

При компьютерной обработке информации упорядоченные каким либо образом данные принято хранить в базах данных

База данных - это набор информации, сохраненный в особых файлах, использование которых вместе со специальными программными средствами позволяет пользователю как просматривать необходимую информацию, так и, по мере необходимости, манипулировать ею, например, добавлять, изменять, копировать, удалять, сортировать и т.д.

Пожалуй, одним из самых банальных примеров баз данных может быть записная книжка с телефонами ваших знакомых. Наверное, у вас есть сейчас или когда-либо была эта полезная вещь. Этот список фамилий владельцев телефонов и их телефонных номеров, представленный в вашей записной книжке в алфавитном порядке, представляет собой, вообще говоря, проиндексированную базу данных. Использование индекса - в данном случае фамилии (или имени) позволяет вам достаточно быстро отыскать требуемый номер телефона.

Структура базы данных

Телефонный справочник представляет собой так называемую “плоскую” базу данных, в которой вся информация располагается в единственной таблице. Каждая запись в этой таблице содержит идентификатор конкретного человека - имя и фамилию и его номер телефона. Таким образом таблица состоит из записей, информация в которых разделена на несколько частей - полей. В данном случае полями являются “ФИО” и “Номер телефона”, как показано на рис.1.1.

Рис.1.1. Таблица, запись и поле.

В отличие от плоских, реляционные базы данных состоят из нескольких таблиц, связь между которыми устанавливается с помощью совпадающих значений одноименных полей.

Здесь следует отметить, что использование реляционной модели баз данных не является единственно возможным способом представления информации. В настоящее время существует несколько различных моделей представления данных, которые, однако, пока не получили такого широкого распространения среди разработчиков и пользователей, как реляционная модель. То есть при разработке систем управления базами данных реляционная модель практически является стандартом.

В качестве примера реляционной базы данных можно привести поставляемую вместе с Visual Basic базу данных BIBLIO.MDB, содержащую библиографическую информацию о книгах по программированию, их авторах и издательствах, эти книги опубликовавших.

Так как Visual Basic использует ту же систему управления базами данных (MS Jet Engine), что и MS Access, то несмотря на наличие в Visual Basic средств работы со многими форматами БД, все таки в приложениях предпочтительно использовать файлы баз данных в формате MS Access. Эти файлы имеют расширение MDB и здесь в основном будут описаны приемы работы с файлами именно такого формата.

Перейдем теперь к исследованию базы данных с библиографией. Для этого откройте файл BIBLIO.MDB при помощи MS Access или VisData.

Содержимое файла базы данных BIBLIO.MDB показано на рис.1.2. В базу данных входят таблицы (Tables), запросы (Queries), формы (Forms), отчеты (Reports), макросы (Macros) и модули (Modules). Макросы, формы и модули нам не интересны, так как это вотчина разработчиков, применяющих Visual Basic for Applications или, сокращенно, VBA.

Рис.1.2. Содержимое файла BIBLIO.MDB

Из рисунка видно, что база данных состоит из таблиц: PUBLISHERS, AUTHORS и TITLES. Каждая из таблиц содержит информацию об объектах одного типа. Из названий таблиц становиться понятно, что данные в каждой таблице принадлежат одной и той же группе объектов. Каждая строка в этих таблицах однозначно определяет один объект из соответствующей группы. Вообще, база данных может состоять из одной или нескольких таблиц. Запись, в свою очередь, состоит из нескольких полей, каждое из которых содержит элемент данных об объекте.

Типы данных, которые можно поместить в таблицу, зависят от формата файла базы данных. В таблице 1.1 приведены некоторые типы данных, которые поддерживаются системой управления базами данных Visual Basic для файлов MS Access.

Таблица 1.1

Название	Описание
Text	Строки алфавитно-цифровых символов. Например, адрес, номер телефона, почтовый индекс и т.п. Текстовое поле может содержать от 0 до 255 символов.
Memo	Длинные строки. Например, комментарии. Максимальный размер ограничен 1.2 Гбайт.
Yes/No	Yes/No, True/False, On/Off, 0 или 1.
Byte	Целые числа в диапазоне от 0 до 255.
Integer	Целые числа в диапазоне от -32768 до +32767.
Long	Целые числа в диапазоне от -2147483648 до 2147483647.
Single	Вещественные числа в диапазоне от -3.4? 10³⁸ до 3.4? 10³⁸.
Double	Вещественные числа в диапазоне от -1.8? 10³⁰⁸ до 1.8? 10³⁰⁸.
Date/Time	Дата и время.
Currency	Используется для обозначения денежных сумм. Запоминаются 11 знаков слева от десятичной точки и 4 знака справа от десятичной точки.
Counter	Длинные целые с автоматическим приращением.
OLE	OLE-объекты, созданные в других программах с использованием протокола OLE. Размер ограничен 1.2 Гбайт.
Binary	Любой двоичный объект размером до 1.2 Гбайт. Этот тип обычно используется для хранения рисунков и двоичных файлов.

Таблица PUBLISHERS (Издатели) содержит информацию об издательствах (имя компании, ее адрес, телефон, факс и др.). На рис. 1.3 и 1.4 показаны структура таблицы PUBLISHERS и ее содержимое в табличном виде.

Рис.1.3. Структура таблицы PUBLISHERS

Рис.1.4. Содержимое таблицы PUBLISHERS

Таблица AUTHORS (Авторы) содержит информацию о авторах - ФИО и год рождения. Структура этой таблицы и ее содержимое показаны на рис.1.5 и 1.6 соответственно.

Рис.1.5. Структура таблицы AUTHORS

Рис.1.6. Содержимое таблицы AUTHORS

Таблица TITLES (Заголовки) содержит данные о самих книгах - название книги, год издания, код ISBN, издатель, краткое описание и др. Структура таблицы TITLES и ее содержимое показаны на рис.1.7 и 1.8 соответственно.

Рис.1.7. Структура таблицы TITLES

Рис.1.8. Содержимое таблицы TITLES

Из рис.1.2 видно, что в базе данных BIBLIO.MDB присутствует еще и таблица TITLE AUTHOR. На первый взгляд непонятно зачем она нужна. Ведь в базе данных есть таблица TITLES с заголовками книг и таблица AUTHORS с данными об авторах. Однако все же эта таблица нужна и для чего она так необходима станет понятно, когда в дальнейшем будем рассматривать отношения между таблицами.

Отношения между таблицами

Отношения между таблицами устанавливают связь между данными находящимися в разных таблицах базы данных.

Отношения между таблицами определяются отношением между группами объектов соответствующего типа. Например, один автор может написать несколько книг и издать их в разных издательствах. Или издательство может опубликовать несколько книг разных авторов. Таким образом, между авторами и названиями книг существует отношение один-ко-многим, а между издательствами и авторами существует отношение много-ко-многим.

Отношения между таблицами базы данных BIBLIO.MDB показаны на рис.1.9.

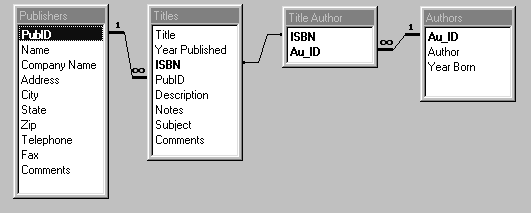
Рис.1.9. Отношения между таблицами базы данных BIBLIO.MDB.

Отношение один-к-одному

Если между двумя таблицами существует отношение один-к-одному, то это означает, что каждая запись в одной таблице соответствует только одной записи в другой таблице.

Примером такого отношения может служить отношение между таблицами. Таблица AUTHORS (Авторы) рассмотрена выше (рис. 1.5 и 1.6) и содержит краткую информацию о авторах (ФИО и год рождения). Таблица PERSON (Личность) содержит персональную информацию о авторах (домашний адрес, телефон, образование и др.) Структура таблицы PERSON показана на рис.1.10. Следует отметить, что в базе данных BIBLIO.MDB никакой таблицы PERSON нет и мы упоминаем о ней только как о иллюстрации отношения между таблицами - один-к-одному.

Рис.1.10. Структура таблицы PERSON

Между таблицами AUTHORS и PERSON существует отношение один-к-одному, так как одна запись, идентифицирующая автора, однозначно соответствует только одной записи в таблице PERSON, содержащей персональные данные об авторе.

Связь между таблицами определяется с помощью совпадающих полей: Au_ID в таблице AUTHORS и в таблице PERSON.

Отношение один-ко-многим

Хорошим примером отношения между таблицами один-ко-многим является отношение между авторами и названиями книг (таблицы AUTHORS и TITLES), так как каждый автор может иметь отношение к созданию нескольких книг. Связь между таблицами AUTHORS и TITLES осуществляется с помощью совпадающих полей Au_ID в обеих таблицах.

Аналогичное отношение существует между издательствами и названиями изданных книг, организацией и работающими в ней сотрудниками, автомобилем и деталями, из которых он состоит и т.п. Понятно, что подобный тип отношения между таблицами наиболее часто встречается при проектировании структуры баз данных.

Отношение много-к-одному

Отношение много-к-одному полностью аналогично рассмотренному выше отношению один-ко-многим.

Отношение много-ко-многим

При отношении между двумя таблицами много-ко-многим каждая запись в одной таблице связана с несколькими записями в другой таблице и наоборот. Иллюстрацией такого отношения может служить отношение между таблицами PUBLISHERS и AUTHORS. С одной стороны, каждое издательство может публиковать книги разных авторов и с другой стороны - каждый автор может публиковаться в разных издательствах.

Для удобства работы с таблицами, имеющими отношение много-ко-многим, обычно в базу данных добавляют еще одну таблицу, которая находится в отношении один-ко-многим и много-к-одному к соответствующим таблицам. В случае базы данных BIBLIO.MDB такой таблицей является TITLE AUTHOR.

Нормализация баз данных

Рассмотрим процесс нормализации базы данных на примере базы данных BIBLIO.MDB. Вообще говоря, все данные о книгах, авторах и издательствах можно разместить в одной таблице, названной, например, BIBLIOS. Структура этой таблицы показана на рис. 1.11. В принципе, можно работать и с такой таблицей. С другой стороны понятно, что такая структура данных является неэффективной. В таблице BIBLIOS будет достаточно много повторяющихся данных, например сведения об издательстве или авторе будут повторяться для каждой опубликованной книги. Такая организация данных приведет к следующим проблемам, с которыми столкнется конечный пользователь вашей программы:

Наличие повторяющихся данных приведет к неоправданному увеличению размера файла базы данных. Кроме нерационального использования дискового пространства, это также вызовет заметное замедление работы приложения.

Ввод пользователем большого количества повторяющейся информации неизбежно приведет к возникновению ошибок.

Изменение, например, номера телефона издательства потребует значительных усилий по корректировке каждой записи, содержащей данные об издателе.

Рис.1.11. Структура таблицы BIBLIOS.

Если, при проектировании приложения для работы с базами данных, вы организуете свои данные таким нерациональным образом, то в дальнейшем вам, скорее всего, больше не поручат решение аналогичных задач.

Чтобы избежать всех этих проблем, надо стремиться максимально уменьшить количество повторяющейся информации. Процесс уменьшения избыточности информации в базе данных посредством разделения ее на несколько связанных друг с другом таблиц и называется нормализацией данных.

Вообще говоря, существует строгая теория нормализации данных, в рамках которой разработаны алгоритмы уменьшения избыточности информации, определены несколько уровней нормализации и установлены критерии, определяющие соответствие данных определенному уровню нормализации. Знакомство с теорией нормализации данных выходит за рамки этих уроков и тем читателям, которым интересно побольше узнать об этом, можно посоветовать обратиться к специальной литературе.

Для того, чтобы построить достаточно эффективную структуру данных, достаточно придерживаться нескольких простых правил:

1. Определите таблицы таким образом, чтобы записи в каждой таблице описывали объекты одного и того же типа. В нашем случае библиографические данные можно разместить в трех таблицах:

PUBLISHERS - содержит информацию об издательствах;
AUTHORS - содержит информацию об авторах книг;
TITLES - содержит информацию об изданных книгах.

2. Если в вашей таблице появляются поля, содержащие аналогичные данные, разделите таблицу.

3. Не запоминайте в таблице данных, которые могут быть вычислены при помощи данных из других таблиц.

4. Используйте вспомогательные таблицы. Например, если в вашей таблице есть поле Страна, то может быть стоит ввести вспомогательную таблицу Country, которая будет содержать соответствующие записи (Россия, Украина, США и т.п.). Этот прием также поможет уменьшить количество ошибок при вводе данных, допускаемых пользователями.

Ключи и индексы

Как было отмечено выше при описании отношений между таблицами, в реляционных базах данных таблицы связываются друг с другом посредством совпадающих значений ключевых полей. Ключевым полем может быть практически любое поле в таблице. Ключ может быть первичным (primary) или внешним (foreign).

Первичный ключ однозначно определяет запись в таблице. В примере с базой данных BIBLIO.MDB таблицы PUBLISHERS, AUTHORS и TITLES имеют первичные ключи PubID, Au_ID и ISBN соответственно. Таблица TITLES также имеет два внешних ключа PubID и Au_ID для связи с таблицами PUBLISHERS и AUTHORS. Таким образом, первичный ключ однозначно определяет запись в таблице, в то время как внешний ключ используется для связи с первичным ключом другой таблицы.

Ключевой поле может иметь определенный смысл, как например ключ ISBN в таблице TITLES. Однако, очень часто ключевое поле не несет никакой смысловой нагрузки и является просто идентификатором объекта в таблице. Во многих случаях удобно использовать в качестве ключа поле счетчика (Counter field). При этом вся ответственность по поддержанию уникальности ключевого поля снимается с пользователя и перекладывается на процессор баз данных. Поле счетчика представляет собой четырехбайтовое целое число (Long) и автоматически увеличивается на единицу при добавлении пользователем новой записи в таблицу.

Данные запоминаются в таблице в том порядке, в котором они вводятся пользователем. Это, так называемый, физический порядок следования записей. Однако, часто требуется представить данные в другом, отличном от физического, порядке. Например может потребоваться просмотреть данные об авторах книг, упорядоченные по алфавиту. Кроме того, часто необходимо найти в большом объеме информации запись, удовлетворяющую определенному критерию. Простой перебор записей при поиске в большой таблице может потребовать достаточно много времени и поэтому будет неэффективным.

Одними из основных требований, предъявляемым к системам управления базами данных, являются возможность представления данных в определенном, отличном от физического, порядке и возможность быстрого поиска определенной записи. Эффективным средством решения этих задач является использование индексов.

Индекс представляет собой таблицу, которая содержит ключевые значения для каждой записи в таблице данных и записанные в порядке, требуемом для пользователя. Ключевые значения определяются на основе одного или нескольких полей таблицы. Кроме того, индекс содержит уникальные ссылки на соответствующие записи в таблице. На рис.1.12 показан фрагмент таблицы CUSTOMERS, содержащей информацию о покупателях, и индекс IDX_NAME, построенный на основе поля Name таблицы CUSTOMERS. Индекс IDX_NAME содержит значения ключевого поля Name, упорядоченные в алфавитном порядке, и ссылки на соответствующие записи в таблице CUSTOMERS.

Рис.1.12. Связь между таблицей и индексом.

Каждая таблица может иметь несколько различных индексов, каждый из которых определяет свой собственный порядок следования записей. Например, таблица AUTHORS может иметь индексы для представления данных об авторах, упорядоченные по дате рождения или по алфавиту. Таким образом, каждый индекс используется для представления одних и тех же данных, но упорядоченных различным образом.

Вообще говоря, таблицы в базе данных могут и не иметь индексов. В этом случае для большой таблицы время поиска определенной записи может быть весьма значительным и использование индекса становиться необходимым. С другой стороны, не следует увлекаться созданием слишком большого количества индексов, так как это может заметно увеличить время необходимое для обновления базы данных и значительно увеличить размер файла базы данных.

При разработке приложений, работающих с базами данных, наиболее широко используются простые индексы. Простые индексы используют значения одного поля таблицы. Примером простого индекса в базе данных BIBLIO.MDB может служить код ISBN, идентификатор автора Au_ID или идентификатор издательства PubID.

Хотя в большинстве случаев для представления данных в определенном порядке достаточно использовать простой индекс, часто возникают ситуации, где не обойтись без использования составных индексов. Составной индекс строится на основе значений двух или более полей таблицы. Хорошей иллюстрацией использования составных индексов может служить база данных родственников при генеалогических исследованиях какой-либо фамилии. Понятно, что использование в качестве простого индекса фамилии человека в данном случае недопустимо. Даже использование составного индекса, основанного на полях имени, фамилии и отчества может быть неэффективным, так как и в этом случае все равно возможно существование достаточно большого числа однофамильцев. Выходом из положения может быть использование составного индекса, основанного, например, на следующих полях таблицы: имя, фамилия, отчество, город и номер телефона.