2.6.1 Коэффициент детерминации. Для оценки качества построенной модели регрессии можно использовать коэффициент детерминации  . Коэффициент детерминации может быть вычислен по формуле:
. Коэффициент детерминации может быть вычислен по формуле:
 .
.
С другой стороны, для парной линейной регрессии верно равенство:
 .
.
При близости значения коэффициента детерминации к 1 говорят, что уравнение регрессии статистически значимо и фактор  оказывает сильное воздействие на результирующий признак
оказывает сильное воздействие на результирующий признак 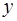 .
.
При анализе модели парной линейной регрессии по значению коэффициента детерминации можно сделать следующие предварительные выводы о качестве модели:
¾ Если  , то будем считать, что использование регрессионной модели для аппроксимации зависимости между переменными
, то будем считать, что использование регрессионной модели для аппроксимации зависимости между переменными 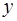 и
и  статистически необоснованно.
статистически необоснованно.
¾ Если  , то использование регрессионной модели возможно, но после оценивания параметров модель подлежит дальнейшему многостороннему статистическому анализу.
, то использование регрессионной модели возможно, но после оценивания параметров модель подлежит дальнейшему многостороннему статистическому анализу.
¾ Если  , то будем. считать, что у нас есть основания для использования регрессионной модели при анализе поведения переменной
, то будем. считать, что у нас есть основания для использования регрессионной модели при анализе поведения переменной 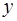 .
.
Средняя ошибка аппроксимации.
Другой показатель качества построенной модели –– среднее относительное отклонение расчетных значений от фактических или средняя ошибка аппроксимации:
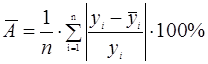 .
.
Построенное уравнение регрессии считается удовлетворительным, если значение 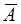 не превышает 10% – 12%.
не превышает 10% – 12%.
Пример.
По 21 региону страны изучается зависимость розничной продажи телевизоров (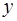 ) от среднедушевого денежного дохода в месяц (
) от среднедушевого денежного дохода в месяц ( ).
).
| Номер региона | Среднедушевой денежный доход в месяц, тыс. руб., 
| Объем розничной продажи телевизоров, тыс. шт., 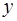
|
| 2,4 | 21,3 | |
| 2,1 | ||
| 2,6 | 23,3 | |
| 1,7 | 15,8 | |
| 2,5 | 21,9 | |
| 2,4 | ||
| 2,6 | ||
| 2,8 | 23,9 | |
| 2,6 | ||
| 2,6 | 24,6 | |
| 2,5 | ||
| 2,9 | ||
| 2,6 | ||
| 2,2 | ||
| 2,6 | ||
| 3,3 | 31,9 | |
| 3,9 | ||
| 35,4 | ||
| 3,7 | ||
| 3,4 |
Необходимо найти зависимость, наилучшим образом отражающую связь между переменными  и
и 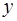 .
.
Рассмотрим вопрос применения модели линейной регрессии в этой задаче.
Построим поле корреляции, т.е. нанесем исходные данные на координатную плоскость. Для этого воспользуемся, например, возможностями MS Excel 2003.
Подготовим таблицу исходных данных.
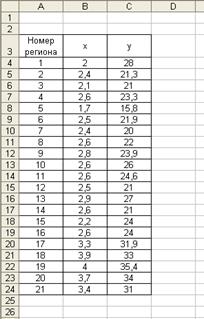
Нанесем на координатную плоскость исходные данные:

Характер расположения точек на графике дает нам основание предположить, что искомая функция регрессии линейная:  . Для оценки коэффициентов уравнения регрессии необходимо составить и решить систему нормальных уравнений ().
. Для оценки коэффициентов уравнения регрессии необходимо составить и решить систему нормальных уравнений ().
По исходным данным рассчитываем необходимые суммы:
| Номер региона | 
| 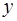
| 
| 
| 
|
| 2,4 | 21,3 | 51,12 | 5,76 | 453,69 | |
| 2,1 | 44,1 | 4,41 | |||
| 2,6 | 23,3 | 60,58 | 6,76 | 542,89 | |
| 1,7 | 15,8 | 26,86 | 2,89 | 249,64 | |
| 2,5 | 21,9 | 54,75 | 6,25 | 479,61 | |
| 2,4 | 5,76 | ||||
| 2,6 | 57,2 | 6,76 | |||
| 2,8 | 23,9 | 66,92 | 7,84 | 571,21 | |
| 2,6 | 67,6 | 6,76 | |||
| 2,6 | 24,6 | 63,96 | 6,76 | 605,16 | |
| 2,5 | 52,5 | 6,25 | |||
| 2,9 | 78,3 | 8,41 | |||
| 2,6 | 54,6 | 6,76 | |||
| 2,2 | 52,8 | 4,84 | |||
| 2,6 | 62,4 | 6,76 | |||
| 3,3 | 31,9 | 105,27 | 10,89 | 1017,61 | |
| 3,9 | 128,7 | 15,21 | |||
| 35,4 | 141,6 | 1253,16 | |||
| 3,7 | 125,8 | 13,69 | |||
| 3,4 | 105,4 | 11,56 | |||
| Сумма | 57,4 | 530,1 | 1504,46 | 164,32 | 13926,97 |
Составляем систему уравнений:

Имеем систему линейных алгебраических уравнений, которая может быть решена, например, по формулам Крамера. Для этого вычислим следующие определители:



Тогда, согласно теореме Крамера,
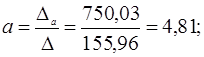

Получаем уравнение регрессии:

Величина коэффициента регрессии  означает, что увеличение среднедушевого месячного дохода на 1 тыс. руб. приведет к увеличение объема розничной продажи в среднем на 7 540 телевизоров. Коэффициент
означает, что увеличение среднедушевого месячного дохода на 1 тыс. руб. приведет к увеличение объема розничной продажи в среднем на 7 540 телевизоров. Коэффициент  в данном случае не имеет содержательной интерпретации.
в данном случае не имеет содержательной интерпретации.
Оценим тесноту линейной связи между переменными и качество построенной модели в целом.
Для оценки тесноты линейной зависимости рассчитаем коэффициент детерминации. Для этого необходимо провести ряд дополнительных вычислений.
Прежде всего, найдем выборочное среднее  по формуле:
по формуле:
 .
.
Для рассматриваемого примера имеем:

Теперь произведем расчет остальных вспомогательных величин:
| Номер региона | 
| 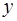
| 
| 
| 
| 
| 
|
| 19,76 | 8,24 | 67,89 | 2,76 | 7,60 | |||
| 2,4 | 21,3 | 22,75 | -1,45 | 2,11 | -3,94 | 15,55 | |
| 2,1 | 20,51 | 0,49 | 0,24 | -4,24 | 18,00 | ||
| 2,6 | 23,3 | 24,25 | -0,95 | 0,90 | -1,94 | 3,77 | |
| 1,7 | 15,8 | 17,52 | -1,72 | 2,95 | -9,44 | 89,17 | |
| 2,5 | 21,9 | 23,50 | -1,60 | 2,56 | -3,34 | 11,17 | |
| 2,4 | 22,75 | -2,75 | 7,57 | -5,24 | 27,49 | ||
| 2,6 | 24,25 | -2,25 | 5,04 | -3,24 | 10,52 | ||
| 2,8 | 23,9 | 25,74 | -1,84 | 3,39 | -1,34 | 1,80 | |
| 2,6 | 24,25 | 1,75 | 3,08 | 0,76 | 0,57 | ||
| 2,6 | 24,6 | 24,25 | 0,35 | 0,13 | -0,64 | 0,41 | |
| 2,5 | 23,50 | -2,50 | 6,24 | -4,24 | 18,00 | ||
| 2,9 | 26,49 | 0,51 | 0,26 | 1,76 | 3,09 | ||
| 2,6 | 24,25 | -3,25 | 10,54 | -4,24 | 18,00 | ||
| 2,2 | 21,26 | 2,74 | 7,53 | -1,24 | 1,54 | ||
| 2,6 | 24,25 | -0,25 | 0,06 | -1,24 | 1,54 | ||
| 3,3 | 31,9 | 29,48 | 2,42 | 5,86 | 6,66 | 44,32 | |
| 3,9 | 33,96 | -0,96 | 0,93 | 7,76 | 60,17 | ||
| 35,4 | 34,71 | 0,69 | 0,47 | 10,16 | 103,17 | ||
| 3,7 | 32,47 | 1,53 | 2,34 | 8,76 | 76,69 | ||
| 3,4 | 30,23 | 0,77 | 0,60 | 5,76 | 33,14 | ||
| Сумма | 57,4 | 530,1 | 130,68 | 545,73 |
Здесь столбец « » – это значения
» – это значения  ,
,  рассчитанные с помощью построенного уравнения регрессии, столбцы «
рассчитанные с помощью построенного уравнения регрессии, столбцы « » и
» и  – это столбцы, так называемых, «остатков»: разностей между исходными значениями
– это столбцы, так называемых, «остатков»: разностей между исходными значениями  ,
,  и рассчитанными с помощью уравнения регрессии
и рассчитанными с помощью уравнения регрессии  , а также их квадратов, а в последних двух столбцах – разности между исходными значениями
, а также их квадратов, а в последних двух столбцах – разности между исходными значениями  , выборочным средним
, выборочным средним  , а также их квадраты.
, а также их квадраты.
Для вычисления коэффициента детерминации воспользуемся формулой ():

Значение коэффициента детерминации позволяет сделать предварительный вывод о том, что у нас имеются основания использовать модель линейной регрессии в данной задаче, поскольку  .
.
Построим линию регрессии на корреляционном поле, для чего добавим на координатной плоскости точки, соответствующие уравнению регрессии ( ).
).

Нанесем теперь уравнение регрессии на диаграмму, используя специальные средства Excel. Для этого необходимо выделить правой кнопкой мыши исходные точки и выбрать опцию Добавить линию тренда.

В открывшемся меню Параметры линии тренда выбрать Линейную аппроксимацию. Далее поставить флажок напротив полей Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации  .
.
Нажав на ОК, получаем еще одну прямую на диаграмме, которая совпадает с построенными ранее точками линии регрессии:
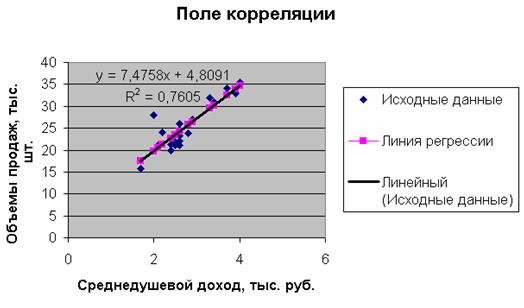
Сплошная черная линия на диаграмме – это линия регрессии, рассчитанная средствами Excel. Линия регрессии, построенная нами ранее, совпала с данной линией регрессии. Нетрудно убедиться, что уравнение регрессии и коэффициент детерминации тоже совпадают с полученными ранее вручную.
Найдем теперь среднюю ошибку аппроксимации для оценки погрешности модели. Для этого нам потребуется вычислить еще ряд промежуточных величин:
| Номер региона | 
| 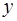
| 
| 
| 
|
| 19,76 | 8,24 | 0,29 | |||
| 2,4 | 21,3 | 22,75 | -1,45 | 0,07 | |
| 2,1 | 20,51 | 0,49 | 0,02 | ||
| 2,6 | 23,3 | 24,25 | -0,95 | 0,04 | |
| 1,7 | 15,8 | 17,52 | -1,72 | 0,11 | |
| 2,5 | 21,9 | 23,50 | -1,60 | 0,07 | |
| 2,4 | 22,75 | -2,75 | 0,14 | ||
| 2,6 | 24,25 | -2,25 | 0,10 | ||
| 2,8 | 23,9 | 25,74 | -1,84 | 0,08 | |
| 2,6 | 24,25 | 1,75 | 0,07 | ||
| 2,6 | 24,6 | 24,25 | 0,35 | 0,01 | |
| 2,5 | 23,50 | -2,50 | 0,12 | ||
| 2,9 | 26,49 | 0,51 | 0,02 | ||
| 2,6 | 24,25 | -3,25 | 0,15 | ||
| 2,2 | 21,26 | 2,74 | 0,11 | ||
| 2,6 | 24,25 | -0,25 | 0,01 | ||
| 3,3 | 31,9 | 29,48 | 2,42 | 0,08 | |
| 3,9 | 33,96 | -0,97 | 0,03 | ||
| 35,4 | 34,71 | 0,69 | 0,02 | ||
| 3,7 | 32,47 | 1,53 | 0,05 | ||
| 3,4 | 30,23 | 0,77 | 0,02 |
Здесь столбец « » – это значения
» – это значения  ,
,  рассчитанные с помощью построенного уравнения регрессии, столбец «
рассчитанные с помощью построенного уравнения регрессии, столбец « » – это столбец так называемых «остатков»: разностей между исходными значениями
» – это столбец так называемых «остатков»: разностей между исходными значениями  , и рассчитанными с помощью уравнения регрессии
, и рассчитанными с помощью уравнения регрессии  ,
,  и, наконец, последний столбец «
и, наконец, последний столбец « » – это вспомогательный столбец для вычисления элементов суммы по формуле (). Просуммируем теперь элементы последнего столбца и разделим полученную сумму на 21 – общее количество исходных данных:
» – это вспомогательный столбец для вычисления элементов суммы по формуле (). Просуммируем теперь элементы последнего столбца и разделим полученную сумму на 21 – общее количество исходных данных:
 .
.
Переведем это число в проценты и запишем окончательное выражение для средней ошибки аппроксимации:
 .
.
Итак, средняя ошибка аппроксимации оказалась около 8%, что говорит о небольшой погрешности построенной модели. Данную модель, с учетом неплохих характеристик ее качества, вполне можно использовать для прогноза – одной из основных целей эконометрического анализа. Предположим, что среднедушевой месячный доход в одном из регионов составит 4,1 тыс. руб. Оценим, каков будет уровень продаж телевизоров в этом регионе согласно построенной модели? Для этого необходимо выбранное значение фактора  подставить в уравнение регрессии ():
подставить в уравнение регрессии ():
 (тыс. руб.),
(тыс. руб.),
т.е. при таком уровне дохода, розничная продажа телевизоров составит, в среднем, 35 480 телевизоров.






