На рис. 3 приведены энергетические диаграммы трех потенциальных барьеров прямоугольного типа, туннелирование через которые будут рассмотрены в данной главе. С целью получения высоких интенсивностей туннелирования будем исследовать тонкие барьеры с 
= 1 нм. Аналитическое выражение для расчета коэффициента туннелирования через барьер первого вида хорошо известно, и может быть записано в виде
, (2.1)
где 
– величина волнового вектора электрона, 
– его энергия, 
, – ширина барьера, 
и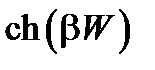 
– соответственно, функции гиперболических синуса и косинуса.
| Случай 1 |
| E |
| U |
| W |
| Случай 3 |
| E |
| U 2 |
| U 1 |
| W |
| W2 |
| W1 |
| Случай 2 |
| E |
| U 2 |
| U 1 |
| W |
| W2 |
| W1 |
Рис. 3. Исследуемые потенциальные барьеры.
Получим аналитические выражения для расчета коэффициента прохождения для остальных двух рассматриваемых барьеров. Следует учесть, что процесс туннелирования через любой потенциальный барьер определяется условием непрерывности волновых функций электрона и их первых производных в областях как перед барьером 
и после него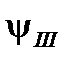 
, так и внутри самого барьера 
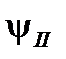. Это условие обычно можно записать в виде
, (2.2)
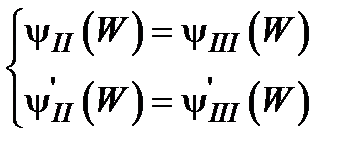. (2.3)
Волновая функция электрона перед барьером 
состоит из падающей и отраженной волны и записывается как 
. Волновая функция электрона после барьера состоит только из прошедшей волны и может быть записана как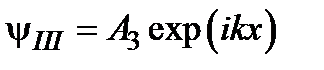 
. Коэффициент прохождения (туннелирования) электрона через потенциальный барьер легко рассчитывается с помощью следующего выражения
. (2.4)
Что же касается волновой функции электрона внутри барьера 
, то она может быть найдена только с помощью решения уравнения Шредингера.
Для барьеров случаев 2 и 3 волновую функцию внутри барьера необходимо разбить на две самостоятельные функции 
и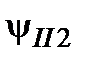 
для каждой из частей барьера со своей высотой и шириной – U 1, W 1 и U 2, W 2. Для них условия (2.2) – (2.3) перепишутся следующим образом
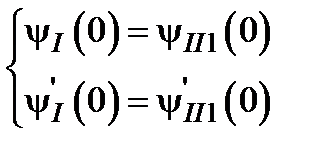, (2.5)
, (2.6)
. (2.7)
Так как части барьера в целом прямоугольные и прохождение над барьерами не рассматривается, то волновые функции в них и 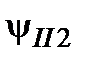можно искать в следующем виде: для барьера случая 2 
при любых условиях, а 
при 
и 
при 
и для барьера случая 3 
при и 
при , а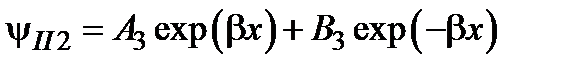 
при обоих условиях. В этих выражениях 
, а 
, если , и 
, если .
Подставив эти решения в системы (2.5) – (2.7), можно найти коэффициенты 
и 
, а подставив их в (2.4), получим выражения для коэффициента туннелирования. Общий их вид оказался одинаковым для обоих барьеров и может быть записан согласно следующему соотношению
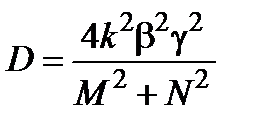. (2.8)
Однако в этом соотношении коэффициенты 
и 
для и различаются, при чем для каждого из барьеров они отличаются только перестановкой отдельных параметров.
При для барьера случая 2 имеем
, (2.9)
, (2.10)
а для барьера случая 3, соответственно,
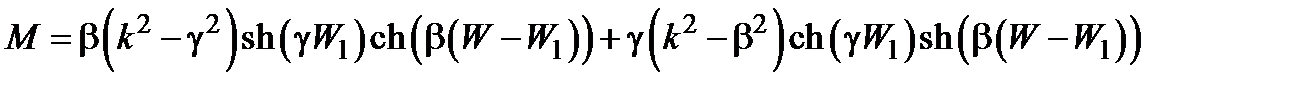, (2.11)
. (2.12)
При для барьера случая 2 имеем
, (2.13)
, (2.14)
а для барьера случая 3, соответственно,
, (2.15)
, (2.16)
