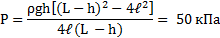При решении аналитических задач на газовые законы надо:
1. Убедиться, что при изменении состояния масса газа остается постоянной.
2. Сделать схематический чертеж, на котором условно отметить состояния газа параметрами Р, V, Т. Записать закон Клапейрона для данных двух состояний.
3. Если какой-либо параметр при переходе газа из одного состояния в другое остается неизменным (могут меняться все три параметра), то уравнение Клапейрона перевести в закон Бойля — Мариотта, Гей-Люссака или Шарля.
4. В случае, когда газ заключен в цилиндрический сосуд и объем газа меняется только за счет изменения высоты его столба h, уравнение Клапейрона можно сразу записывать в виде:
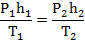
5. Используя условия задачи, определить термодинамические параметры, выразив их через заданные величины. И если газ граничит с жидкостью, то особое внимание следует обратить на определение давления. Для его определения тех случаях, когда газ производит давление на жидкость, следует использовать закон Паскаля: провести нулевой уровень через границу, отделяющую газ от жидкости, и записать уравнение равновесия жидкости.
6. Полученную систему уравнений решить относительно неизвестной величины.
P.S.
§ Если в задаче рассматривают состояния нескольких газов, отделенных друг от друга поршнями или входящих в состав смеси, то все указанные действия нужно проделать для каждого газа отдельно.
§ В задачах на газовые законы используется только абсолютная температура.
При увеличении абсолютной температуры газа в 2 раза давление увеличилось на 25%. во сколько раз изменился объем газа?
| Т2=2Т1 Р2=1,25Р1 | Запишем уравнение Клапейрона, так как меняются все три параметра идеального газа: |
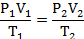|  С учетом данных, уравнение принимает вид:
|
Газ изотермически сжат от объема V1 = 8 л до объема V2 = 6 л. Давление при этом возросло на DР = 4∙103 Па. Определить первоначальное давление.
Запишем уравнение Клапейрона и, так как процесс изотермический, переведем его в закон Бойля-Мариотта
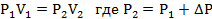
Поэтому можно записать:
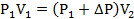
Отсюда находим первоначальное давление:
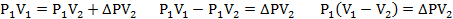
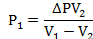
И объемы газов можно оставить в литрах, не переводить в систему СИ.
При нагревании газа при постоянном давлении на 1К его объем увеличился на 5% от первоначального. При какой температуре находился газ?
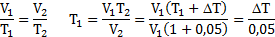
Сколько ртути войдет в стеклянный баллончик объемом V0, нагретый до Т0, если плотность ртути при температуре Т равна ρ.
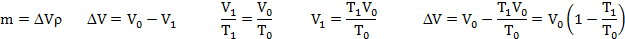
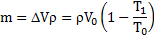
Закрытый с обоих концов цилиндрический сосуд разделен на две равные части теплонепроницаемым поршнем. Длина каждой части 42см. В обеих половинках находится одинаковое количество азота при температуре 27°С и давлении 1 атмосфера. На сколько надо нагреть газ в одной части сосуда, чтобы поршень переместился на 2 см?
| I |
| II |
| x |
Для газа в отделе I:
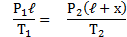
Для газа в отделе II:
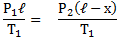
Отсюда следует:
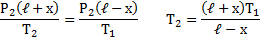
Объем баллона, содержащего газ под давлением 1,2·105 Па составляет 6 литров. Каким станет давление газа, если этот баллон соединить с другим баллоном объем которого 10 литров и он практически не содержит газа.
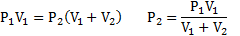
Два одинаковых стеклянных шара соединены трубкой. При 0° С капелька ртути находится посередине трубки. Объем воздуха в каждом шаре и части трубки У= 200 см3. На какое расстояние х сместится капелька, если один шар нагреть на 2° С, а другой на столько же охладить? Поперечное сечение трубки S=20 мм2
| I |
| II |
| x |
Для газа в отделе I:
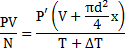
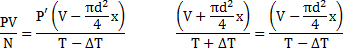
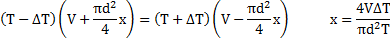
Температура воздуха в цилиндре 7°С. На сколько переместиться поршень при нагревании воздуха на 20К, если ℓ1=14см?
| ℓ |
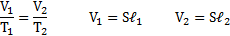
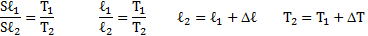
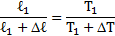
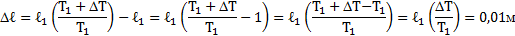
Газ граничит с жидкостью
Электрическая лампа наполнена азотом при давлении Р= 600 мм рт. ст. Объем лампы V = 500 см3. Какая масса воды войдет в лампу, если у нее отломить кончик под водой? Атмосферное давление 760 мм рт. ст.?
Объем воды, поступившей в сосуд равен изменению объема газа при изотермическом процессе. Вода будет заходить в колбу до тех пор, пока давление внутри колбы не станет равным давлению наружному, то есть атмосферному.
Запишем закон Бойля-Мариотта для газа в колбе:%
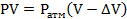
Отсюда определим изменение объема:
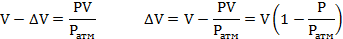
Масса поступившей воды равна:
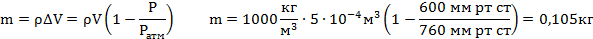
Объем пузырька воздуха по мере всплывания со дна озера на поверхность увеличивается в 3 раза. Какова глубина озера?
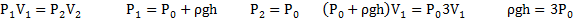
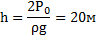
Открытую стеклянную трубку длиной ℓ=1м наполовину погружают в ртуть.Затем трубку закрывают пальцем и вынимают из ртути. Какой длины столбик ртути останется в трубке? атмосферное давление нлормальное.
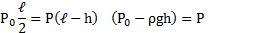
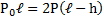
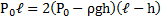
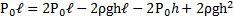
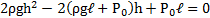
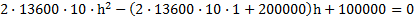
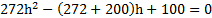
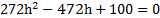
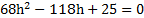
Узкая вертикальная цилиндрическая трубка длиной L,закрытая с одного конца, содержит воздух, отделенный от наружного воздуха столбиком ртути длиной h. Плотность ртути ρ. Трубка расположена открытым концом вверх. Какова была длина ℓ столбика воздуха в трубке, если при перевертывании трубки открытым концом вниз, из трубки вылилось половина ртути. атмосферное давление Р0
| h |
| ℓ |
| h/2 |
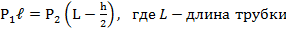
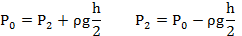
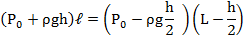
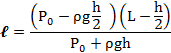
В стеклянной трубке, запаянной с одного конца и расположенной горизонтально, находится столбик воздуха длиной 300мм, закрытый столбиком ртути длиной 200мм. На сколько изменится длина воздушного столбика, если трубку расположить открытым концом вверх? Атмосферное давление нормальное.
| Р1V1 |
| Р2V2 |
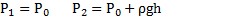
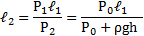
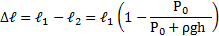
Длинная пробирка открытым концом погружена в сосуд с ртутью. При температуре t1 = 47 °С уровни ртути в пробирке и в сосуде совпадают. Над уровнем ртути остается часть пробирки длины L = 76см. На какую высоту ℓ поднимется ртуть в пробирке, если ее охладить до температуры t2 = -33 °С? Атмосферное давление Р0 = 0,1 МПа.
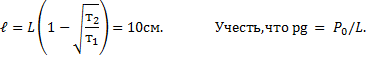
Посередине откачанной и запаянной с обоих концов горизонтально расположенной трубки длины L = 1 м находится столбик ртути длины h = 20 см. Если трубку поставить вертикально, столбик ртути сместится на расстояние ℓ = 10 см. До какого давления Р была откачана трубка? Плотность ртути ρ= 13,6∙103 кг/м3.
В обоих концах трубки воздух первоначально занимал объем
V = S(L - h)/2,
где S - площадь поперечного сечения трубки, и имел давление Р.
Когда трубку поставили вертикально, объем воздуха в верхней части трубки стал
V1 = S[(L - h)/2 + ℓ],
а давление стало Р1;
В нижней части трубки объем стал V2 = S[(L - h)/2 - ℓ], а давление стало равным Р2
Согласно закону Бойля-Мариотта для верхней части трубки PV = P1V2
Откуда (L - h) P =(L-h + 2ℓ)P1;
Для нижней части трубки
PV = P2V2, откуда (L-h)P = (L-h-2ℓ)Р2.
С другой стороны, столбик ртути находится в равновесии, когда давление воздуха в нижней части трубки равно сумме давлений воздуха в верхней части трубки и столбика ртути, т.е.
P2=P1+ρgh
Исключив Р1 иР2 из уравнений, найдем = 50 кПа.
