Регресійний аналіз призначений для вибору форми зв’язку, типу моделі, для визначення розрахункових значень залежності змінної (результативної ознаки).
Методи регресійного та кореляційного аналізів застосовуються у комплексі один з одним.
Рівняння регресії показує як в середньому змінюється у при зміні будь-якого хі та має вигляд:
y = f(x1,..,xn),
де: у – залежна змінна;
хі – незалежні змінні (фактори).
Якщо незалежна змінна одна, то це простий регресійний аналіз, якщо незалежних змінних декілька (n ≥ 2) то такий аналіз називається багатофакторним.
При проведенні регресійного аналізу вирішується дві основні задачі:
1. Побудова рівняння регресії, тобто знаходження виду залежності, між результативним показником і незалежними факторами х1, х2,..,хn.
2. Оцінювання значущості отриманого рівняння, тобто визначення того факту, наскільки обрані результативні показники пояснюють варіацію показника у.
Залежності, що розглядаються, можуть бути не тільки прямими, а й оберненими та нелінійними.
Так, рівняння ух=а+bх є рівнянням лінійної регресії, ступеневій регресії відповідає рівняння ух=ахb, а показниковій – ух=abх.
У багатофакторному аналізі часто використовуються лінійні моделі виду:
yx=a+b1x1+b2x2+…+bnxn.
Головною властивістю рівняння регресії є те, що вона (регресія) мінімізує суму квадратів (дисперсів) відхилень точок на лінії від експериментальних даних.
Побудова рівняння регресії здійснюється, як правило, метода найменших квадратів, тобто
де m – число спостережень.
У лінійній моделі a та b є параметрами регресії, які необхідно визначити. Параметр b відображає середню зміну результативного показника при зміні фактора х, коефіцієнта а виступає як постійна величина результативного показника й не залежить від зміни фактора.
На підставі головної властивості рівняння регресії (4.1.21) і з урахуванням того, що у= а+bх, можливо побудувати функцію двох змінних поки що невідомих параметрів рівняння регресії а та b:
Мінімум функції 
, знайдений з умов, що її часткові похідні дорівнюють нулю, дає таку систему рівнянь
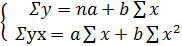(4.1.22)
Розглянемо приклад щодо розрахунку параметрів регресії, використовуючи дані табл. 4.1.3.
Підставимо конкретні похідні величини з таблиці в систему рівнянь:
Розв’язок цієї системи: b = 684,63; а = 5901,39
Отримане рівняння регресії має вигляд:
ух = 5901,39 + 684,63х.
Для математичного відображення криволінійної залежності використовується рівняння гіперболи:
Параметри a i b визначаються за допомогою такої системи рівнянь:
Якщо при збільшенні одного показника значення іншого зростають до певного рівня, а потім починають зменшуватися, то для запису такої залежності найкраще підходить парабола другого порядку:
ух = а + bx + cx2.
Відповідно до вимог методу найменших квадратів для визначення параметрів a, b, i c необхідно розв’язати систему рівнянь:
Якість кореляційно-регресійного аналізу забезпечується виконанням ряду умов, серед яких важливішим є однорідність інформації, що досліджується, значущість коефіцієнта кореляції, надійність рівняння зв’язку (регресії).
Однорідність інформації оцінюється у залежності від відносного розподілу біля середнього рівня. Критеріями служать середньоквадратичне відхилення і коефіцієнт варіації, що обумовлені по кожному факторному і результативному показнику.
Середньоквадратичне відхилення (σ) характеризує абсолютне відхилення індивідуальних значень від середньої арифметичної:
Відносна міра відхилень від середньої арифметичної, чи коефіцієнт варіації (V) визначається за формулою:
Незначною визначається варіація, що не перевищує 10%.
Нетипові спостереження треба виключати з розрахунків, якщо V > 33%.
Значущість коефіцієнта кореляції може бути оцінена за допомогою t – критерія Стьюдента:
Якщо отримане емпіричне значення критерія (te) буде більше критичного табличного значення (te > tтабл), то коефіцієнт кореляції можна визначити значущим.
Значущість коефіцієнтів лінійної регресії (а і b) також може бути встановлено за допомогою t – критерію Стьюдента. Крім того, адекватність однофакторної регресійної моделі можна оцінити за допомогою F – критерію Фішера:
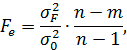
де m - число параметрів у рівнянні регресії,
n - обсяг вибірки, кількість спостережень;
– дисперсія по лінії регресії;
- залишкова дисперсія.
Якщо емпіричне розрахункове значення F – критерію виявиться вище табличного (Fe > Fm), то рівняння регресії треба визначити адекватним.
Розглянемо приклад
Приклади розв’язування задач
1. Поле кореляції Y та Х (млн. грн.) приведено в таблиці.
Необхідно:
а) знайти групові середні та побудувати лінії регресії;
б) оцінити щільність та напрямок зв’язку між змінними, за допомогою коефіцієнта кореляції; перевірити значущість коефіцієнта кореляції та побудувати для нього 95%-ий довірчий інтервал;
в) обчислити емпіричні кореляційні відношення та оцінити їх значущість на 5%-ому рівні;
г) на рівні значущості 0,05 перевірити гіпотезу про лінійну кореляційну залежність між змінними Y та X.
| х | Разом | ||||||
| 0-4,5 | 4,5-9 | 9-13,5 | 13,5-18 | 18-22,5 | |||
| Y | 0-1,4 | ||||||
| 1,4-2,8 | |||||||
| 2,8-4,2 | |||||||
| 4,2-5,6 | |||||||
| 5,6-7 | |||||||
| 7-8,4 | |||||||
| Разом |
Для більшої наочності перепишемо таблицю у такому вигляді:(В таблиці через хj і уi позначені середини відповідних інтервалів, а ni i nj відповідні їх частоти).
| х | |||||||||
| 0-4,5 | 4,5-9 | 9-13,5 | 13,5-18 | 18-22,5 | n1 | ||||
| yi | yj | 2,25 | 6,75 | 11,25 | 15,75 | 20,25 | |||
| Y | 0-1,4 | 0,7 | |||||||
| 1,4-2,8 | 2,1 | ||||||||
| 2,8-4,2 | 3,5 | ||||||||
| 4,2-5,6 | 4,9 | ||||||||
| 5,6-7 | 6,3 | ||||||||
| 7-8,4 | 7,7 | ||||||||
| nj | |||||||||
a) групові середні
для кожного хi
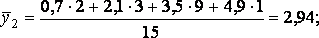
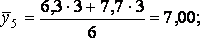
для кожного yj
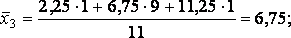
Побудуємо лінії регресії: 
та 
, де вибірковий коефіцієнт регресії
Знайдемо відповідні середні:
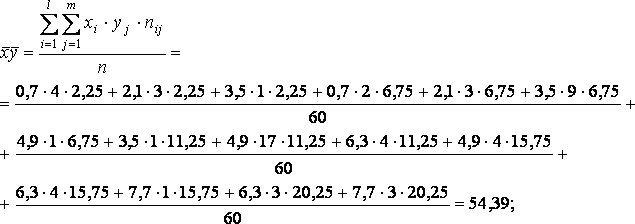
Якщо
б) оцінити щільність та напрямок зв’язку між змінними, за допомогою коефіцієнта кореляції; перевірити значущість коефіцієнта кореляції та побудувати для нього 95%-ий довірчий інтервал.
проте bxу > 0 i byх > 0, тому
З результату знаходження вибіркового коефіцієнту кореляції зробимо висновок, що зв’язок між змінними прямий та має велику щільність.
t0,95;58 = 2;
Так як t > t 0,95;58, то коефіцієнт кореляції значимо відрізняється від нуля.
Ф(t1-a)=0,95;
t0,05 =1,96
це і є 95% довірчий інтервал (0,776;0,914).
в) обчислити емпіричні кореляційні відношення та оцінити їх значущість на 5%-ому рівні;
та 
Знайдемо міжгрупову дисперсію:
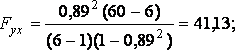
m = 6, n = 60,
F0,05;5;54 = 2,4, звідси F > F0,05;5;54, тобто ηух значимо відрізняється від нуля.
г) на рівні значущості 0,05 перевірити гіпотезу про лінійну кореляційну залежність між змінними Y та X.
Fα;1;n-1 = F0,05;1;58 = 4,01;
Так як F>F0,05;1;58, то r = R значно відрізняється від нуля, що позначає лінійну залежність між змінними X i Y.
Контрольні запитання та завдання
1. Призначення регресійного аналізу, його завдання.
2. Однофакторний і багатофакторний регресійний аналіз.
3. Запишить рівняння регресії для:
а) лінійної залежності, б) криволінійної залежності; в) для залежності ух = а+ bx + cx2.
4. Знайти групові середні та побудувати лінії регресії для завдань п.5 контрольних запитань та завдань попереднього підрозділу.
