Правила сравнения бесконечно малых функций.

Допустим, у нас есть бесконечно малые при одном и том же величины и

Если , то 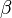— бесконечно малая высшего порядка малости, чем . Обозначают .

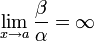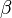Если , то — бесконечно малая низшего порядка малости, чем . Соответственно .

Если (предел конечен и не равен 0), то и 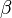являются бесконечно малыми величинами одного порядка малости.

Это обозначается как 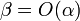или (в силу симметричности данного отношения).

Если (предел конечен и не равен 0), то бесконечно малая величина 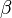имеет -й порядок малости относительно бесконечно малой .

Первый замечательный предел.

Предел отношения sinxк xпри равен 1.

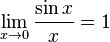
Доказательство?

Второй замечательный предел.

или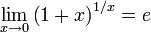

Доказательство?

 

Определения непрерывности функции.

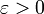Функция называется непрерывной на отрезке, если она непрерывна в каждой точке этого отрезка.Функция непрерывна в точке , если для любого существует такое, что для любого

 

 

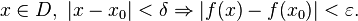
Точки разрыва функции и их классификация.

Точка называется точкой разрыва функции f(x), если f(x) не определена в точке или не является непрерывной в этой точке.

Точка называется точкой разрыва 1-го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы. (скачок)

Точка называется точкой разрыва 2–го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

 

 

 

Тема 4. Дифференциальное исчисление функции одной переменной.

1. Производная функции одной переменной, её геометрический и физический смысл.

Производной называется предел отношения приращения функции к приращению аргумента.

Физ. Смысл- производная расстояния = скорости, производная скорости = ускорению.

Геом. Смысл – производная – это тангенс угла наклона касательной, проведенной к графику этой функции в данной точке.

Непрерывность функции одной переменной, имеющей конечную производную.

Теорема. Если функция дифференцируема в некоторой точке a, то она непрерывна в этой точке.

Доказательство. По определению производной

Это предельное равенство означает, что выражение под знаком предела можно представить в виде

где α(x) – бесконечно малая функция при x → a. Тогда

Следовательно, при x → a.

 

Уравнение касательной и нормали к графику.

Уравнение касательной: . Прямая, проходящая через точку касания, является касательной.

Уравнение нормали: Нормалью называется прямая, перпендикулярная костельной и проходящая через точку косания.