Определение 8. Интервалы, в которых функция 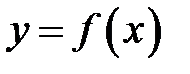 сохраняет определенный знак, называются интервалами знакопостоянства данной функции.
сохраняет определенный знак, называются интервалами знакопостоянства данной функции.
Очевидно, что график функции лежит выше оси абсцисс, когда 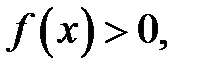 и ниже, когда
и ниже, когда 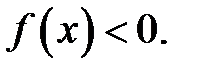 Функция меняет свой знак при переходе через нули функции или через точки разрыва. На интервале, где функция непрерывна и не имеет нулей, ее знак сохраняется.
Функция меняет свой знак при переходе через нули функции или через точки разрыва. На интервале, где функция непрерывна и не имеет нулей, ее знак сохраняется.
2.7.1. Алгоритм нахождения интервалов знакопостоянства
1) Найти область определения функции 
2) Решить уравнение  корни уравнения, входящие в
корни уравнения, входящие в  будут являться нулями функции.
будут являться нулями функции.
3) На числовую прямую нанести область определения функции и нули функции. В полученных интервалах определить знак функции.
4) Указать интервалы знакопостоянства функции.
Пример 2.5. Найти интервалы знакопостоянства функции.
а) 
Решение.
1. Область определения функции 

2. Решим уравнение 
 Нулями функции являются точки
Нулями функции являются точки 


| Знак функции у |
| -2/3 |
| _ |
| + |
| + |
| _ |
| х |

|

|

|
Рис. 3. Промежутки знакопостоянства
4. Функция принимает положительные значения (график выше оси  ) при
) при 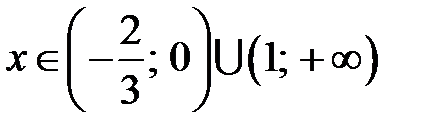 и отрицательные значения (график ниже оси
и отрицательные значения (график ниже оси  ) при
) при 
б) 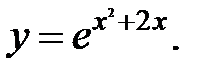
Решение.
1. Область определения функции 

2. Решим уравнение  Корней нет, следовательно, нулей функции нет.
Корней нет, следовательно, нулей функции нет.
3. Функция принимает положительные значения при любом значении переменной  входящем в область определения функции, т. е. график функции лежит выше оси абсцисс.
входящем в область определения функции, т. е. график функции лежит выше оси абсцисс.
Непрерывность функции
Определение 9. Пусть функция  определена в точке
определена в точке  и в некоторой окрестности этой точки. Функция
и в некоторой окрестности этой точки. Функция  называется непрерывной в точке
называется непрерывной в точке  если
если 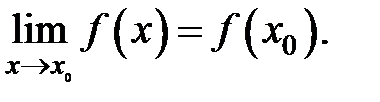
Должны выполняться три условия непрерывности функции в точке 
1) функция определена в точке 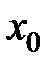 и ее окрестности;
и ее окрестности;
2) существуют конечные односторонние пределы в точке 



3) односторонние пределы в точке  равнымежду собой и равны значению функции в этой точке:
равнымежду собой и равны значению функции в этой точке: 
Замечание.
Если в точке  нарушается хотя бы одно из трех указанных условий, то функция в точке
нарушается хотя бы одно из трех указанных условий, то функция в точке  терпит разрыв.
терпит разрыв.
Определение 10. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.
Определение 11. Точка разрыва  называется точкой разрыва первого рода функции
называется точкой разрыва первого рода функции  если в этой точке существуют конечные односторонние пределы функции, т.е.
если в этой точке существуют конечные односторонние пределы функции, т.е.  и
и  При этом: а) если
При этом: а) если  или
или  не определено, то точка
не определено, то точка  называется точкой устранимого разрыва (рис. 3, а); б) если
называется точкой устранимого разрыва (рис. 3, а); б) если  то точка
то точка  называется точкой конечного разрыва (рис. 3, б). Величину, равную
называется точкой конечного разрыва (рис. 3, б). Величину, равную  называют скачком функции в точке разрыва первого рода.
называют скачком функции в точке разрыва первого рода.
Определение 12. Точка разрыва  называется точкой разрыва второго рода функции
называется точкой разрыва второго рода функции  если по крайней мере один из односторонних пределов не существует или равен бесконечности (рис. 4, в).
если по крайней мере один из односторонних пределов не существует или равен бесконечности (рис. 4, в).
|
|
|
Теорема3.Всякая элементарная функция непрерывна в каждой точке области ее определения.
2.8.1. Алгоритм исследования функции на непрерывность
1. Найти область определения функции: 
2. Определить точки разрыва.
3. Найти односторонние пределы в точках разрыва.
4. Выяснить характер разрыва.
Пример 2.6. Исследовать функцию на непрерывность: 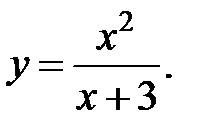
1. Найдем область определения функции 
 кроме
кроме 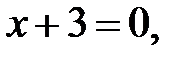
 т. е.
т. е. 
2. Точка  является точкой разрыва.
является точкой разрыва.
3. Найдем односторонние пределы:


4. Следовательно, точка  − точка разрыва 2-го рода.
− точка разрыва 2-го рода.
Асимптоты графика функции
Определение 13. Асимптотой графика функции 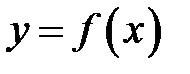 называется прямая линия, обладающая тем свойством, что расстояние от точки
называется прямая линия, обладающая тем свойством, что расстояние от точки  до этой прямой стремится к нулю при неограниченном удалении точки графика от
до этой прямой стремится к нулю при неограниченном удалении точки графика от
вертикальная асимптоты | начала координат (т. е. прямая, к которой кривая графика неограниченно приближается).
Различают вертикальные, горизонтальные и наклонные асимптоты.
Определение 14. Будем говорить, что прямая  является вертикальной асимптотой графика функции является вертикальной асимптотой графика функции 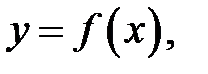 если если  (рис. 5). (рис. 5).
|
Т е о р е м а 4. Прямая 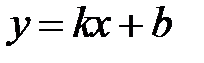 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  (рис. 5) тогда и только тогда, когда существуют конечные пределы
(рис. 5) тогда и только тогда, когда существуют конечные пределы 
 Если хотя бы один из пределов не существует (или равен бесконечности), то график функции не имеет наклонной асимптоты.
Если хотя бы один из пределов не существует (или равен бесконечности), то график функции не имеет наклонной асимптоты.
Замечания.
1. Из определения следует, что вертикальные асимптоты нужно искать в точках бесконечного разрыва функции (в точках разрыва второго рода). При приближении  к точке разрыва
к точке разрыва  (хотя бы с одной из сторон – слева или справа)
(хотя бы с одной из сторон – слева или справа)  стремится к бесконечностии график функции неограниченно приближается к прямой
стремится к бесконечностии график функции неограниченно приближается к прямой 
2. График функции может иметь любое число вертикальных асимптот или вообще не иметьих.
3. Для выяснения вопроса о наличии асимптоты следует отдельно рассматривать пределы при  и
и  В связи с этим функция может
В связи с этим функция может
− иметь одну и ту же наклонную асимптоту при  (рис.6, а);
(рис.6, а);
− иметь разные наклонные асимптоты при  и
и  (рис. 6, б);
(рис. 6, б);
−иметь наклонную асимптоту только при  или при
или при  (рис. 6, в).
(рис. 6, в).
4. Частным случаем наклонной асимптоты (при  )является горизонтальная асимптота. Прямая является горизонтальной асимптотой графика функции
)является горизонтальная асимптота. Прямая является горизонтальной асимптотой графика функции 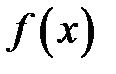 при
при  тогда и только тогда, когда
тогда и только тогда, когда 
5. График функции может пересекаться с наклонной и горизонтальнойасимптотами в конечном или бесконечном числе точек.
| у |
| х |
| х |
| х |
| О |
| у |
| у |
| О |
| О |
| Рис. 6. Примеры расположения наклонных асимптот |
| а |
| б |
| в |
2.9.1. Алгоритм нахождения асимптот
1) Найти область определения функции.
2)Определить наличие точек разрыва второго рода(см. замечание 1).
3) Для уравнения наклонной асимптоты  найти
найти 
 (если они существуют). Сделать вывод.
(если они существуют). Сделать вывод.
П р и м е р 2.7. Найти асимптоты графика функции:
а) 
Решение.
1) Найдем область определения функции 

2) Уравнение вертикальной асимптоты  так как
так как  (т. е. в точке
(т. е. в точке  − разрыв второго рода).
− разрыв второго рода).
3) Уравнение наклонной асимптоты 



Итак,  − наклонная асимптота графика функции.
− наклонная асимптота графика функции.
б) 
Решение.
1) 

2)  − вертикальная асимптота, так как
− вертикальная асимптота, так как 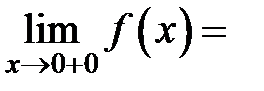
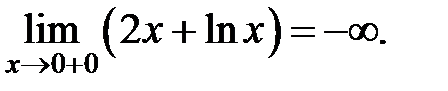
3) Выясним вопрос о наличии наклонной асимптоты при  так как функция определена лишь при
так как функция определена лишь при 

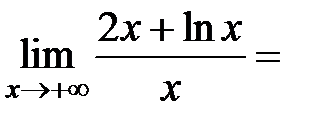

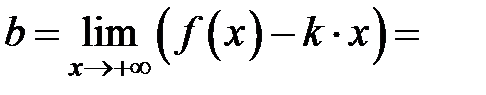
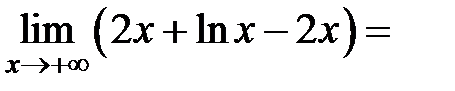

Следовательно, график данной функции не имеет наклонной асимптоты (см. теорему 4).









