СОДЕРЖАНИЕ
Лабораторная работа №1 ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ТИПОВЫХ ЗВЕНЬЕВ.. 4
Лабораторная работа № 2 ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК САУ 10
Лабораторная работа № 3 ОЦЕНКА КАЧЕСТВА ПЕРЕХОДНОГО ПРОЦЕССА САУ 14
Лабораторная работа № 4 ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ САУ............................................................................................18
Лабораторная работа №5 УЛУДШЕНИЕ КАЧЕСТВА РЕГУЛИРОВАНИЯ САУ ВЕДЕНИЕМ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ.....................................................................................................24
Лабораторная работа №6 УЛУДШЕНИЕ КАЧЕСТВА РЕГУЛИРОВАНИЯ САУ ПАРАЛЛЕЛЬНЫМИ КОРРЕКТИРУЮЩИМИ ЗВЕНЬЯМИ, ОБРАТАНЫМИ СВЯЗЯМИ И КОМБИНИРОВАННЫМ
УПРАВЛЕНИЕМ..............................................................................................29
Лабораторная работа №7 ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ КОНТРОЛЛЕРЫ ПЛК-100,ПЛК-150........................................................................35
Лабораторная работа №8 ПРОГРАММИРОВАНИЕ ОВЕН ПЛК-100........42
Лабораторная работа №9 ИСПОЛЬЗОВАНИЕ КОНТРОЛЛЕРА ОВЕН
ПЛК-100 ДЛЯ УПРАВЛЕНИЯ ДВИЖЕНИЕМ РОБОТА МП-9С..............52
ТРЕБОВАНИЯ К СОДЕРЖАНИЮ ОТЧЕТА.. 57
ПРИЛОЖЕНИЕ. 58
Лабораторная работа №1
ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК
ТИПОВЫХ ЗВЕНЬЕВ
Цель работы. Изучение временных и частотных характеристик типовых звеньев систем автоматического управления. Исследование влияния изменения параметров передаточных функций звеньев на их характеристики.
Содержание работы
Для расчета систем автоматического управления (САУ) они разбиваются на динамические звенья. Под динамическим звеном понимают устройство любого физического вида, но описываемое определенным дифференциальным уравнением. В соответствии с этим звенья классифицируются именно по виду дифференциального уравнения, или что то же, по виду передаточной функции звена. Под типовым звеном понимается звено, описываемое дифференциальным уравнением не выше второго порядка:
.
При нулевых начальных условиях (т.е. если для t <0 входная и выходная величины, а также их производные тождественно равны нулю) передаточная функция звена может быть найдена как отношение изображений по Лапласу выходной и входной величин
,
где p=c+j ω– комплексная величина.
При известной передаточной функции звена изображение по Лапласу его выходной величины можно найти из выражения
.
Динамические свойства звена определяются по его временным и частотным характеристикам. Наиболее распространенными временными характеристиками являются переходная характеристика и функция веса.
Переходная функция, или переходная характеристика h(t), представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход единичного скачкообразного воздействия (рис. 1,а). Такое входное воздействие называется единичной ступенчатой функцией (рис. 1,б):
а) б)
Рис.1. Переходная функция:
а - единичное скачкообразное воздействие 1 (t); б – переходная характеристика h(t)
Функция веса w(t) представляет собой реакцию звена на единичную импульсную функцию (рис. 2,а). Единичная импульсная функция, или дельта-функция (рис. 2,б), представляет собой производную от единичной ступенчатой функции
Основное свойство дельта функции заключается в том, что 
, т.е. она имеет единичную площадь.
а) б)
Рис.2. Функция веса:
а - единичный импульс d (t); б – функция веса w(t)
При описании линейных систем или звеньев важное значение имеют частотные характеристики. Они описывают установившиеся вынужденные колебания в системе при подаче на ее вход гармонического воздействия. В общем случае уравнение линейной системы можно записать так:
.
Ее передаточная функция имеет вид
.
Функцию W(j w ), которую получают из передаточной функции W(p) при подстановке в нее p=j w, называют частотной передаточной функцией
.
Частотная передаточная функция является комплексной функцией от действительной переменной w, которая называется частотой.
Функцию W(j w ) можно представить в виде
,
где
.
Если 
, то 
.
На комплексной плоскости частотная передаточная функция W(j w ) определяет вектор, длина которого равна A( w ), а аргумент, т.е. угол, образованный этим вектором с действительной положительной полуосью - j ( w ). Кривую, которую описывает конец этого вектора при изменении частоты от 0 до ¥ (иногда от -¥ до ¥), называют амплитудно-фазовой частотной характеристикой (АФЧХ).
Модуль 
называют амплитудной частотной функцией, а ее график – амплитудной частотной характеристикой.
Аргумент называют фазовой частотной функцией, а ее график фазовой частотной характеристикой.
Кроме перечисленных частотных характеристик, используют еще логарифмическую амплитудную частотную характеристику (ЛАЧХ) и логарифмическую фазовую частотную характеристику (ЛФЧХ). При построении графиков этих характеристик по оси абсцисс откладывают логарифм частоты lgw. Единицей логарифма частоты является декада. Декадой называется интервал, на котором частота изменяется в 10 раз. Для графика ЛАЧХ по оси ординат откладывается функция 
, а для графика ЛФЧХ – функцию 
. Ось ординат проводят через произвольную точку, а не через точку w=0, так как lgw ® - ¥ при w ® 0. Пример графиков ЛЧХ приведен на рис.3. Основные типовые звенья САУ приведены в табл. 1.
Рис.3. Логарифмические частотные характеристики
Порядок выполнения работы
1. Набрать модель звена.
2. Получить семейства графиков переходных характеристик звена при изменении:
- коэффициента передачи K =1…10;
- постоянных времени звена T =0,1…1;
- коэффициента демпфирования x=0,1…1.
3. По полученным графикам определить основные показатели переходных характеристик:
- величину установившегося значения h уст;
- длительность переходного процесса t пер;
- перерегулирование s (
).
4. Получить семейства графиков частотных характеристик звена (АФЧХ, ЛАЧХ, ФЧХ) при параметрах, указанных в п.2.
5. Провести сравнительный анализ полученных характеристик, сделать выводы о влиянии параметров передаточных функций звеньев на их динамические характеристики.
Таблица 1
Основные типовые звенья САУ
| Позиционные | |
| 1. Безынерционное | 
|
| 2. Апериодическое первого порядка | 
|
| 3. Апериодическое второго порядка | 
|
| 4. Колебательное | 
|
| 5. Консервативное | 
|
| Интегрирующие | |
| 1. Идеальное интегрирующее | 
|
| 2. Интегрирующее с замедлением | 
|
| 3. Изодромное | 
|
| Дифференцирующие | |
| 1. Идеальное дифференцирующее | 
|
| 2. Дифференцирующее с замедлением | 
|
Контрольные вопросы
1. Какие временные характеристики САУ вы знаете и какова их связь с передаточными функциями САУ?
2. Какие виды частотных характеристик САУ вам известны и какой их физический смысл?
3. Какие типовые динамические звенья вы знаете, их передаточные функции и дифференциальные уравнения?
4. Как влияют параметры передаточных функций звеньев на их временные и частотные характеристики?
5. Каким образом выполняется расчет переходного процесса на выходе звена при произвольном входном воздействии по переходной и импульсной характеристикам?
6. Как получить частотные характеристики звеньев по их передаточным функциям?
7. Как строятся логарифмические частотные характеристики?
Лабораторная работа № 2
ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК САУ
Цель работы. Изучение частотных характеристик САУ (АФЧХ и ЛАФЧХ); исследование указанных характеристик при изменении параметров звеньев САУ.
Содержание работы
Частотные характеристики описывают установившиеся вынужденные колебания на выходе системы, вызванные гармоническим воздействием на ее входе. Основные виды частотных характеристик приведены в лабораторной работе №1.
В результате разбиения САУ на звенья и определения их математического описания в виде передаточных функций, частотных или переходных характеристик составляется структурная схема системы. По структурной схеме затем получают передаточную функцию или характеристики САУ в целом.
Наиболее просто описание САУ (передаточную функцию) можно найти, оперируя передаточными функциями звеньев. При последовательном соединении передаточная функция цепочки звеньев W(p) равна произведению передаточных функций звеньев
,
где Wi(p) – передаточная функция i -го звена, n – количество звеньев.
Передаточная функция группы параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев
.
Если звено с передаточной функцией W1(p) охвачено обратной связью через звено W ос (p), то передаточная функция такого замкнутого контура W(p) определяется выражением
.
Здесь знак плюс в знаменателе соответствует отрицательной обратной связи, а минус – положительной.
На основании приведенных формул каждая группа звеньев может быть заменена одним эквивалентным звеном, а вся система управления приведена к одноконтурному виду.
Связь между частотными характеристиками системы и составляющих ее звеньев определяется выражением передаточной функции W(p), если подставить в него p=j w.
Соответственно АФЧХ цепочки последовательно соединенных звеньев разомкнутой САУ равна
,
где Wi(jw) – АФЧХ i -го звена САУ.
Отсюда: 
,
,
где A( w ) и j ( w ) – амплитудная и фазовая частотные характеристики САУ, а Ai( w ) и j i( w ) – соответствующие характеристики i -го звена.
Логарифмирование A( w ) дает выражение для ЛАЧХ цепочки звеньев L( w )
,
где Li( w ) – ЛАЧХ отдельного звена.
Асимптотическая ЛАЧХ цепочки звеньев строится сразу без построения ЛАЧХ отдельных звеньев. Порядок построения следующий:
1. Вначале откладывается ордината общей ЛАЧХ при w=1, равная 
, где k – коэффициент передачи всей цепочки звеньев, равный произведению коэффициентов передачи каждого звена.
2. Через найденную точку проводится асимптота с наклоном 20(m-r) дб/дек, где m – число дифференцирующих, а r – число интегрирующих звеньев.
3. На оси абсцисс откладывают значения сопрягающих частот, равных 1/ Ti, где Ti – постоянные времени звеньев.
4. Первая асимптота проводится от оси ординат до первой сопрягающей частоты. В этой точке производится ее излом с изменением наклона в соответствии с типом звена, которому принадлежит данная сопрягающая частота.
5. Таким же образом характеристика продолжается в сторону увеличения частоты, претерпевая соответствующие изломы на каждой сопрягающей частоте. Ординаты ЛФЧХ цепочки звеньев суммируются.
В результате предельное значение j ( w ) при j®¥ будет равно (n-m)p/2, где n – порядок дифференциального уравнения цепочки звеньев, m – число дифференцирующих звеньев.
Построение АФЧХ цепочки звеньев непосредственно по АФЧХ отдельных звеньев осуществляется путем перемножения векторов Wi(j w ) при одинаковых значениях частоты (модули Ai перемножаются, а фазы j I – складываются).
Порядок выполнения работы
1. Для САУ, структурная схема которой показана на рис.4, получить выражения передаточной функции, частотной передаточной функции и частотных характеристик (W(j w ), A( w ), j ( w ), L( w )).
2. Набрать модель разомкнутой САУ, структурная схема которой показана на рис.4, со следующими значениями параметров: k 1=5; T 1=0,1; k 2=1; T 2=0,5; k 3=0,1; T 3=0,6; ξ=0,5.
3. Наблюдать и зафиксировать ЛАЧХ, ФЧХ и АФЧХ разомкнутой системы, состоящей только из звеньев 1 и 2, при изменении:
- общего коэффициента передачи 
,
где ki – коэффициент передачи i -го звена, n – количество звеньев, k =1…10;
- постоянной времени T 1=0,05…0,5;
- постоянной времени T 2=0,2…1,0;
- постоянной времени T 3=0,1…0,6;
- коэффициента демпфирования x = 0,1…0,8.
Рис.4. Структурная схема САУ
4. Наблюдать и зафиксировать ЛАЧХ, ФЧХ и АФЧХ всей разомкнутой системы, приведенной на рис.4. Провести сравнительный анализ полученных результатов.
5. Набрать модель замкнутой САУ. Получить выражения передаточных функций и частотных характеристик (Ф(j w ), A( w ), j ( w ), L( w )) замкнутой системы.
6. Наблюдать и зафиксировать ЛАЧХ, ФЧХ и АФЧХ замкнутой системы при изменении параметров, указанных в пп. 3 и 4 (k ос=1).
7. Провести сравнительный анализ частотных характеристик замкнутой и разомкнутой САУ.
Контрольные вопросы
1. Какие вы знаете виды соединения звеньев САУ?
2. Как определяются передаточные функции и частотные характеристики различных соединений звеньев?
3. Как построить ЛАЧХ цепочки звеньев САУ?
4. Каким образом выполняется приведение САУ к одноконтурному виду?
5. Как строится АФЧХ звеньев и их соединений?
6. Как получить частотные характеристики САУ по передаточной функции?
7. Каково влияние параметров звеньев САУ на ее частотные характеристики?
Лабораторная работа № 3
ОЦЕНКА КАЧЕСТВА ПЕРЕХОДНОГО ПРОЦЕССА САУ
Цель работы. Исследование качества переходных процессов замкнутой САУ; определение показателей качества по переходному процессу и корневым критериям; исследование влияния на качество переходных процессов параметров САУ.
Содержание работы
Переходные процессы, возникающие в системах при скачкообразных воздействиях, принято делить на три группы: монотонные, апериодические и колебательные.
Характеристики, приведенные на рис. 10,а соответствуют ступенчатому изменению задающего воздействия, в соответствии с которым выходная величина y системы по окончании переходного процесса получает приращение y уст, а на рис. 10,б – внешнему воздействию в виде возмущения.
а) б)
Рис. 10. Переходные характеристики САУ:
а – от задающего воздействия; б – от возмущающего воздействия.
У монотонных процессов первая производная выходной величины 
не меняет знак (кривая 1 на рис. 10), у апериодических знак производной меняется не более одного раза (кривая 2 на рис. 10), а у колебательных – первая производная меняет свой знак периодически (теоретически бесконечное число раз) (кривая 3 на рис. 10). Кривая 4 на рис. 10 характеризует неустойчивую систему, и переходный процесс называется расходящимся.
Качество переходных процессов численно характеризуется следующими показателями качества.
Время переходного процесса t п– интервал времени от начала переходного процесса до момента, когда отклонение выходной величины от ее нового установившегося значения становится меньше определенной величины (обычно 5% величины скачка на входе).
Перерегулирование s – максимальное отклонение в переходный период относительно нового установившегося значения
.
Колебательность – число колебаний, равное числу минимумов кривой переходного процесса в интервале времени t п.
Качество переходных процессов зависит не только от собственных свойств системы (ее структуры и параметров звеньев), но и от внешнего воздействия (места его приложения, величины, характера изменения во времени). Кроме того, качество переходного процесса зависит также от начальных условий, т.е. от состояния системы в момент приложения воздействия.
В одной и той же системе переходный процесс при одном воздействии может быть не колебательным, а при другом – иметь недопустимо большую колебательность. Более того, переходный процесс, вызванный одним и тем же воздействием, может в широких пределах изменять свои показатели при изменении начальных условий.
Таким образом, при оценке качества переходных процессов необходимо указать воздействие и начальные условия, при которых имеет место данное качество. При общей характеристике качества переходных процессов в системе его обычно оценивают для единичного ступенчатого воздействия при нулевых начальных условиях, т.е. для переходной характеристики.
Исчерпывающее представление о качестве переходных процессов дает сама кривая процесса y(t).
Оценить в общем качество переходных процессов при всевозможных воздействиях и начальных условиях можно по корневым критериям. Эта группа критериев основана на оценке качества по значениям полюсов и нулей передаточной функции системы, т.е. корням ее знаменателя и числителя. Для оценки быстродействия системы используется степень устойчивости h, которая равна абсолютному значению вещественной части ближайшего к мнимой оси корня.
На рис. 11 показан случай, когда ближайшим к мнимой оси является действительный корень. В равной мере это может быть и пара сопряженных комплексных корней.
Корни характеристического уравнения, расположенные ближе всего к мнимой оси, т.е. имеющие наименьшую по абсолютной величине вещественную часть, дают самую длительную составляющую переходного процесса. При этом длительность всего переходного процесса определяется выражением
| Рис. 11. Расположение корней характеристического уравнения САУ |
.
Склонность системы к колебаниям определяется комплексными корнями характеристического уравнения САУ. Мерой колебательности m является отношение мнимой части корня b к вещественной a:
.
Чем больше m, тем больше колебательность переходного процесса. В комплексной плоскости корень, определяющий наиболее колебательную составляющую, соответствует наибольшему значению угла
,
между лучом, направленным через корень из начала координат, и действительной осью (рис. 10). Качество переходного процесса будет тем лучше, чем больше h и меньше m.
Порядок выполнения работы
1. Набрать схему модели замкнутой САУ, структурная схема которой приведена на рис. 9 с параметрами: k у=10; T у=0,001; k м=3; T м=0,1; T э=0,02; k п=0,01.
2. Получить графики переходных процессов выходной величины y, определить по ним показатели качества (t n, s).
3. Составить передаточную функцию замкнутой САУ и получить распределение нулей и полюсов передаточной функции. Определить степень устойчивости hипоказатель колебательности m.
4. Выполнить задания 2 и 3 при изменении коэффициента k у=5…50. Провести сравнительный анализ полученных результатов.
5. Выполнить задания 2 и 3 при различных значениях постоянной времени Т у = 0,001…0,01 и дать оценку полученным результатам.
Контрольные вопросы
1. Какие существуют показатели качества переходных процессов САУ?
2. Как определяются показатели качества по расположению нулей и полюсов передаточной функции САУ?
3. Как аналитически определить показатели качества?
4. Каковы частотные критерии качества переходных процессов?
5. Какова связь частотных характеристик САУ с качеством ее переходной характеристики?
6. Как влияют параметры САУ на показатели качества?
7. Какие факторы определяют качество переходных процессов САУ?
Лабораторная работа № 4
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ САУ
Цель работы. Исследование устойчивости замкнутых САУ; определение запасов устойчивости по амплитуде и фазе; изучение влияния параметров звеньев, входящих в состав системы, на ее устойчивость; определение предельного коэффициента усиления системы.
Содержание работы
В процессе работы система автоматического управления всегда подвергается действию внешних сил, которые могут вывести ее из состояния равновесия. Устойчивость – это свойство САУ возвращаться в исходный или близкий к нему режим после выхода из него в результате какого-либо воздействия. Это одно из основных условий работоспособности САУ, которое требует, чтобы переходные процессы в ней затухали. На рис. 5. показаны переходные процессы в устойчивой (рис. 5,а) и неустойчивой (рис. 5,б) системах. 
а) б)
Рис. 5. Переходные процессы в САУ:
а – в устойчивой системе; б – в неустойчивой системе.
Характер переходных процессов в САУ определяется корнями характеристического уравнения. Для их затухания необходимо и достаточно, чтобы все корни лежали слева от мнимой оси плоскости корней (имели отрицательные вещественные части). Если хотя бы один корень окажется справа от мнимой оси, то эта система будет неустойчивой. Наличие корня на мнимой оси означает, что система находится на границе устойчивости.
Вычисление корней характеристических уравнений третьего и выше порядков трудоемко, однако для суждения об устойчивости этого обычно не требуется в связи с тем, что разработаны косвенные признаки, по которым можно судить о знаках действительных частей этих корней и тем самым об устойчивости САУ. Эти признаки называются критериями устойчивости. Существуют три основных критерия устойчивости: критерий Рауса-Гурвица, критерий Михайлова и критерий Найквиста. Если записать характеристический полином в виде
и составить из его коэффициентов квадратную матрицу, содержащую n строк и n столбцов
,
то критерий устойчивости Гурвица сводится к тому, что при а 0>0 должны быть больше нуля все n определителей Гурвица, получаемых из квадратной матрицы коэффициентов. Определители Гурвица составляются по следующему правилу
;
;
;
¼.
Последний определитель включает в себя всю матрицу и выражается через предпоследний следующим образом:
.
Однако в устойчивой САУ D n -1 должен быть положительным, поэтому условие положительности последнего определителя сводится к положительности аn. Система находится на границе устойчивости, если D n -1=0 (колебательная граница устойчивости), либо аn =0 (апериодическая граница устойчивости).
Критерий устойчивости Михайлова также основан на рассмотрении характеристического полинома D (p). Если в этот полином подставить чисто мнимые значения р = j w, где w - угловая частота колебаний, то получим характеристический комплекс
.
Здесь X (w), U (w) – соответственно вещественные и мнимые части, а D (w) и Y(w) – модуль и фаза характеристического комплекса.
Характеристический полином не будет иметь корней в правой полуплоскости, если полное приращение фазы Y(w) при изменении w от 0 до ¥ равно 
, где n – степень полинома D (р). Следовательно, САУ будет устойчива. Годограф D (j w) в комплексной плоскости называется годографом (кривой) Михайлова. Кривая Михайлова для устойчивых систем всегда имеет правильную спиралевидную форму, ее конец уходит в бесконечность в том квадрате комплексной плоскости, номер которого равен степени характеристического многочлена n. В неустойчивых САУ нарушается последовательность прохождения квадратов, вследствие чего полное приращение фазы Y(w) оказывается меньшим, чем . На рис. 6 кривая 1 соответствует устойчивой САУ, а кривые 3 и 4 – неустойчивым. Условием нахождения системы на границе устойчивости является прохождение кривой Михайлова через начало координат (кривая 2 на рис. 6).
Критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы по АФЧХ разомкнутой системы. Если известно, что САУ в разомкнутом состоянии устойчива, то условие устойчивости замкнутой системы сводится к требованию, чтобы АФЧХ разомкнутой системы не охватывала точку (-1, j 0). На рис. 7 характеристики 1 и 4 соответствуют устойчивым системам, характеристика 3 – неустойчивой системе, характеристика 2 – нахождению системы на границе устойчивости.
| Рис. 7. Амплитудно-фазовые частотные характеристики САУ |
В соответствии с критерием Найквиста об устойчивости можно судить не только по АФЧХ, но и по логарифмическим характеристикам; ЛАЧХ должна пересечь ось абсцисс раньше, чем ФЧХ окончательно перейдет за значение -p. Или иными словами, на частоте среза wс величина φ (wс) должна быть больше -p. На рис. 8 изображены ЛАЧХ L (w) и четыре варианта φ(w).
Рис. 8. Логарифмические частотные характеристики САУ
В случаях 1 и 4 замкнутая САУ устойчива, 2 – соответствует положению САУ на границе устойчивости, а 3 – неустойчивой замкнутой системе.
При оценке устойчивости систем одного факта устойчивости недостаточно. Необходимо еще оценить величину запаса устойчивости, то есть степень удаленности системы от границы устойчивости. В случае применения критерия Гурвица о запасе устойчивости можно судить по тому запасу, с которым выполняются входящие в него неравенства. При использовании критерия Найквиста запас устойчивости определяется удаленностью АФЧХ от критической точки (-1, j 0). Основное распространение в качестве меры запаса устойчивости получили две величины – запас устойчивости по фазе Dj и запас устойчивости по амплитуде D L, показанные на рис. 8.
Запас устойчивости по фазе определяется величиной Dj, на которую должно возрасти запаздывание по фазе в системе на частоте среза wс, чтобы система оказалась на границе устойчивости. Запас устойчивости по амплитуде D L определяется величиной допустимого подъема ЛАЧХ, при которой система окажется на границе устойчивости. Таким образом, запас по амплитуде представляет собой запас по коэффициенту передачи k разомкнутой системы по отношению к его критическому по устойчивости значению. Критическим (предельным) называют то значение коэффициента k, при котором АФЧХ проходит через критическую точку (-1, j 0), то есть система находится на границе устойчивости.
Порядок выполнения работы
1. Набрать схему модели замкнутой САУ, приведенной на рис. 9, с параметрами: k у=10; T у=0,001; k м=3; T м=0,1; T э=0,02; k п=0,01.
Получить выражения передаточных функций замкнутой и разомкнутой системы, ее частотных характеристик: АФЧХ, L (w), j(w).
2. Получить графики переходной характеристики замкнутой САУ и АФЧХ, ЛАФЧХ разомкнутой САУ. Оценить устойчивость замкнутой САУ (D L, Dj) по полученным кривым.
3. Выполнить задание 2 при различных значениях коэффициента усиления системы k у = 5…50.
4. Определить экспериментально предельный коэффициент усиления системы k пред , добиваясь появления незатухающих гармонических колебаний.
5. Получить графики АФЧХ и ЛАЧХ разомкнутой системы, находящейся в замкнутом состоянии на границе устойчивости (k = k пред).
6. Выполнить задания 4 и 5 для Т у = 0,01 и 0,001. Оценить влияние постоянной времени на устойчивость системы.
7. Изменить порядок астатизма системы, добавив в структурную схему интегрирующее звено. Оценить устойчивость полученной САУ.
8. Сделать вывод о влиянии параметров системы и порядка астатизма на ее устойчивость.
Рис. 9. Структурная схема САУ
Контрольные вопросы
1. Как определяется понятие устойчивости САУ?
2. Какое уравнение называется характеристическим уравнением САУ?
3. Как корни характеристического уравнения влияют на устойчивость системы?
4. Как определяются границы устойчивости САУ?
5. Что такое структурно-неустойчивые системы?
6. Какие Вам известны критерии устойчивости?
7. Как формулируется критерий устойчивости Найквиста для астатических и систем, неустойчивых в разомкнутом состоянии?
8. Что такое логарифмический критерий устойчивости Найквиста?
9. Как определяются области устойчивости САУ? Что такое запас устойчивости САУ?
10. Как влияет значение коэффициента усиления и величина постоянных времени звеньев САУ на ее устойчивость?
Лабораторная работа № 5
УЛУЧШЕНИЕ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ САУ ВВЕДЕНИЕМ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
Цель работы. Изучение вопросов коррекции САУ последовательными корректирующими звеньями; исследование показателей качества (запаса устойчивости, быстродействия, перерегулирования, точности) замкнутой системы автоматического регулирования (САР) при типовых входных воздействиях (ступенчатом, гармоническом, скоростном); сравнение полученных показателей исходной и скорректированной моделей.
Содержание работы
Под улучшением качества процесса регулирования понимается изменение динамических свойств системы с целью получения необходимого запаса устойчивости, быстродействия, точности в типовых режимах.
Получение перечисленных требуемых качественных показаний является единой задачей и ни один из входящих в неё вопросов не решается в отрыве от других. При этом прежде всего необходимо попытаться рациональным образом изменить параметры САУ (коэффициенты передачи отдельных звеньев, постоянные времени и т.п.) так, чтобы удовлетворить требованиям качества регулирования. При невозможности решить эту задачу вариацией параметров имеющейся системы приходится идти на изменение её структуры. Для этого обычно используется введение в систему регулирования корректирующих средств, которые должны изменить её динамику в нужном направлении. Корректирующие устройства (КУ) включают в систему последовательно, параллельно и в виде обратной связи. Использование того или иного типа корректирующих устройств определяется удобством технической реализации.
В линейных системах их динамические свойства при введении корректирующих устройств различного типа можно сделать одинаковыми, а для корректирующего устройства одного типа можно подобрать эквивалентное корректирующее устройство другого типа. Звенья последовательного типа удобно применять в тех случаях, когда в САУ используется электрический сигнал в виде напряжения постоянного тока, величина которого функционально связана с сигналом ошибки. Наиболее распространёнными КУ являются четырёхполюсники из R -, C -, L – элементов, которые разделяют на дифференцирующие, интегрирующие и интегродифференцирующие.
Пассивное дифференцирующее звено имеет передаточную функцию вида
,
где 
, 
– коэффициент передачи звена на нулевой частоте, т.е. в установившемся режиме. По своему действию звено относится к форсирующим, так как переходный процесс в звене форсируется в своей начальной части. Частотная передаточная функция, её модуль и фаза равны соответственно:
;
;
.
Пассивное дифференцирующее звено подавляет низкие частоты. При w=0 коэффициент передачи 
. Верхние частоты пропускаются лучше чем нижние, при 
k стремится к единице. Звено вносит положительный фазовый сдвиг. Важным свойством пассивного дифференцирующего звена является способность уменьшать постоянную времени какого-либо элемента САУ в заданное число раз. Например, при последовательном соединении пассивного корректирующего звена и апериодического звена первого порядка с коэффициентом передачи K 0 и постоянной времени T 0 получим
.
Если T 0 = T 1, то 
.
Таким образом, постоянная времени звена Т 0 уменьшилась в 1/ k раз. Однако во столько же раз оказался сниженным коэффициент передачи звена, что можно компенсировать введением дополнительного усилителя.
Пассивное интегрирующее звено имеет передаточную функцию
.
По своему действию оно относится к замедляющим звеньям. Частотная передаточная функция, её модуль и фаза равны соответственно:
;
;
.
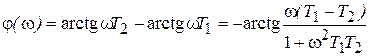Амплитудная характеристика показывает, что звено пропускает низкие частоты с коэффициентом передачи, близким к единице (при w=0, А(w)=1). Высокие частоты подавляются, так при 
получаем 
. Звено вносит отрицательный фазовый сдвиг.
Сравнительный анализ показывает, что пассивное интегрирующее звено противоположно по своему действиюпассивному дифференцирующему звену.
Пассивное интегродифференцирующее звено имеет передаточную функцию
,
причём 
, 
.
Частотная передаточная функция звена, её модуль и фаза равны соответственно:
;
;
.
Из приведённых характеристик видно, что звено при частоте w=0 и имеет коэффициент передачи, равный единице. Подавление входного сигнала происходит в области средних частот. Фазовый сдвиг равен нулю при w=0, 
и 
.
Частота wm соответствует минимальному значению
.
В области низких частот (w < wm) звено имеет отрицательный фазовый сдвиг; в области высоких частот (w > wm) – положительный.
Порядок выполнения работы
1. Набрать схему для моделирования САУ (рис. 12).
Рис. 12. Структурная схема корректируемой САУ.
Модель содержит неизменяемую часть: усилительное устройство 3, исполнительный двигатель 4, главную обратную связь 6 и два последовательных корректирующих звена 1 и 2. Установить следующие параметры неизменяемой части модели: Т у=0,001 с; k м=3; Т м=0,14 с; Т э=0,015 с; k п=0,01.
2. Настроить исходную модель (без коррекции), добиваясь изменением k у усилительного устройства 3 качественного переходного процесса на выходе системы при ступенчатом входном воздействии.
3. Получить графики переходной характеристики; ошибки рассогласования при гармоническом и скоростном входных сигналах; ЛАФЧХ исходной САУ (без коррекции).
4. Скорректировать исходную САУ, используя последовательное пассивное дифференцирующее звено 1 при Т 1=0,05 с; Т 2=0,01 с.
5. Получить переходную характеристику, ошибку рассогласования, ЛАФЧХ скорректированной САУ, а также графики сигналов ошибки при гармоническом и скоростном управляющих воздействиях.
6. Скорректировать исходную САУ, используя последовательное пассивное интегрирующее звено 2 при Т 3=0,08 с, Т 4=0,2 с.
7. Получить переходную характеристику, ошибку рассогласования, ЛАФЧХ и графики ошибки при гармоническом и скоростном управляющих воздействиях скорректированной САУ.
8. Скорректировать исходную САУ двумя последовательными корректирующими звеньями 1 и 2 одновременно, осуществляя интегродифференцирующую коррекцию.
9. Получить переходную характеристику, ошибку рассогласования, ЛАФЧХ и графики ошибки при гармоническом и скоростном управляющих воздействиях.
10. Провести сравнительный анализ исходной и скорректированной различными звеньями САУ.
11. Выполнить расчёт динамических показателей (перерегулирования σ, быстродействия t n, ошибки рассогласования в различных режимах) исходной и скорректированной САУ.
12. Рассчитать по ЛАФЧХ запас устойчивости по амплитуде и фазе исходной и скорректированной различными устройствами системы.
Контрольные вопросы
1. Каковы показатели качества регулирования автоматических систем?
2. Каково назначение и классификация корректирующих устройств?
3. Какие существуют типы последовательных корректирующих устройств?
4. Что такое пассивное интегрирующее звено (назначение, передаточная функция, временные и частотные характеристики, влияние на работу САУ)?
5. Какие характеристики у пассивного дифференцирующего корректирующего устройства?
6. Какое влияние на работу САУ оказывает интегродифференцирующее корректирующее устройство?
8. Как выполняется синтез последовательных корректирующих устройств?
Лабораторная работа № 6
УЛУЧШЕНИЕ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ В САУ ПАРАЛЛЕЛЬНЫМИ КОРРЕКТИРУЮЩИМИ ЗВЕНЬЯМИ, ОБРАТНЫМИ СВЯЗЯМИ И КОМБИНИРОВАННЫМ УПРАВЛЕНИЕМ
Цель работы. Изучение вопросов коррекции САУ параллельными корректирующими устройствами, корректирующими обратными связями, комбинированным управлением по ошибке и управляющему воздействию; исследование показателей качества регулирования САУ с различными видами коррекции при типовых входных воздействиях; сравнение динамических характеристик исходной и скорректированной систем.
Содержание работы
Улучшения качества процесса регулирования можно достичь коррекцией САУ не только последовательными, но и параллельными корректирующими звеньями, обратными связями, введением комбинированного управления.
Параллельные корректирующие звенья удобно применять при использовании сложных законов управления, когда наряду с основным сигналом вводятся его производные и интегралы. Введение интегралов позволяет повысить точность систем регулирования без заметного ухудшения запаса устойчивости. На рис. 13 показана структурная схема САУ при введении изодромного звена.
Рис. 13. Структурная схема САУ с изодромным звеном
Передаточная функция изодромного звена имеет вид
,
где 
- постоянная времени изодромного звена.
Таким образом, включение изодромного звена повышает порядок астатизма, а следовательно, и точность САУ, одновременно при достаточно больших значениях постоянной времени Т и условия устойчивости скорректированной САУ мало отличаются от условий устойчивости исходной системы. Для дальнейшего повышения порядка астатизма САУ можно применить несколько параллельных корректирующих звеньев.
Применение регулирования по производным от ошибок повышает запас устойчивости системы регулирования, что позволяет увеличить общий коэффициент усиления САУ и этим самым улучшить точность регулирования. На рис. 14 приведена структурная схема системы с корректирующим дифференцирующим звеном, включенным параллельно основной цепи.
Такой вид регулирования повышает точность системы и в том случае, когда сохраняется неизменным общий коэффициент усиления, так как система регулирования реагирует не только на наличие ошибки, но и на тенденцию к изменению её величины.
Рис. 14. Структурная схема САУ с дифференцирующим звеном
В качестве корректирующих устройств часто применяют обратные связи (ОС). На рис. 15 представлена схема введения в цепь регулирования звена местной обратной связи передаточной функцией W oc(p), охватывающей определённую часть системы.
Рис. 15. Структурная схема САУ с местной обратной связью
Передаточная функция разомкнутой скорректированной системы
.
Корректирующие ОС широко распространены вследствие простоты их технической реализации. Кроме этого отрицательные обратные связи уменьшают влияние нелинейностей тех участков цепи регулирования, которые ими охватываются. Так как практически все САУ содержат нелинейности, ухудшающие качество регулирования (силы трения, люфт, зону нечувствительности, и т.п.), то использование корректирующих ОС часто позволяет добиться лучших результатов по сравнению с другими типами коррекции.
Обратные связи могут быть жесткими и гибкими. Если W ос(0)=0, то в установившемся режиме передаточная функция цепи, охваченной ОС, будет равна передаточной функции исходной цепи. Такая обратная связь называется гибкой, она действует только в переходных режимах. Если Wос(0)≠0, то ОС действует и в переходном, и в установившемся режимах и называется жесткой. Довольно часто в цепи ОС используют идеальное безынерционное звено с передаточной функцией W ос(р)= k ос. В этом случае коэффициент передачи и постоянная времени внутреннего контура, образованного местной ОС, уменьшается в 1+ k×k ос раз, где k×k ос – коэффициент передачи внутреннего контура.
Отрицательные ОС могут различным образом изменять динамические показания систем управления:
· подавлять высокие частоты (аналоги пассивного последовательного интегрирующего звена);
· подавлять низкие частоты (аналоги пассивного последовательного дифференцирующего звена);
· подавлять средние частоты (аналоги пассивного последовательного интегродифференцирующего звена).
Установить аналогию ОС с любым корректирующим звеном можно, используя формулы перехода, которые легко получить, приравняв результирующие передаточные функции скорректированной системы W ск(р):
,
где W c(p) – передаточная функция части САУ; W пз(p), W п(p) – передаточные функции последовательного и параллельного звеньев соответственно. Отсюда можно получить
,
.
Наибольший интерес представляет переход от последовательного корректирующего звена, параметры которого рассчитываются проще, к эквивалентной обратной связи, предпочтительной с точки зрения технической реализации.
Другим способом улучшения динамических показателей САУ является комбинированное управление, при котором наряду с регулированием по ошибке используется регулирование по управляющему или возмущающему воздействиям. На рис. 16 приведена структурная схема системы с комбинированным управлением по ошибке ε(t) и управляющему воздействию g (t).
Рис. 16. Структурная схема САУ с комбинированным управлением.
При отсутствии регулирования по управляющему воздействию, т.е. при φ(р)=0, регулируемая величена у связана с управляющим воздействием через передаточную функцию замкнутой системы
.
При введении регулирования по управляющему воздействию регулируемая величина определяется выражением
.
Из приведённого выражения видно, что введение регулирования по управляющему воздействию не меняет характеристического уравнения системы, работающей по отклонению ε (знаменатель передаточных функций одинаков), т.е. не будут нарушаться условия устойчивости и показатели качества переходного процесса, определяемые корнями характеристического уравнения. Использование комбинированного управления позволяет ввести первую производную от управляющего воздействия и таким образом получить равной нулю скоростную ошибку в системах с астатизмом первого порядка, т.е. повысить на единицу степень астатизма относительно управляющего воздействия.
Порядок выполнения работы
1. Набрать схему для моделирования САУ, структурная схема которой показана на рис. 17.
Рис. 17. Структурная схема САУ
Схема содержит неизменяемую часть, структура и параметры которой рассмотрены в лабораторной работе № 4, корректирующую обратную связь с передаточной функцией W ос(р), параллельное корректирующее устройство W п(р), звено для регулирования по управляющему воздействию φ(р).
2. Построить исходную модель (без коррекции), добиваясь изменением К у качественного переходного процесса при ступенчатом входном воздействии.
3. Получить и зафиксировать ЛАФЧХ, переходный процесс, ошибку рассогласования и динамические показатели при ступенчатом, гармоническом и скоростном входных сигналах в исходной САУ.
4. Скорректировать исходную САУ параллельным корректирующим звеном при W п(р)= Т д p с параметрами Т д=0,2…1. Зафиксировать перечисленные в п.3 характеристики, наблюдать изменения запасов устойчивости по амплитуде и фазе в скорректированной системе.
5. Скорректировать исходную САУ, включая в её структуру жесткую ОС с W ос(р)= k тг с коэффициентом передачи, изменяющимся в пределах k тг=0,2…3. Зафиксировать графики, указанные в п. 3. Определить изменение коэффициента передачи, постоянной времени и параметра затухания внутреннего контура.
6. Ввести в исходную САУ комбинированное управление φ(р)= k р с параметрами k =0,2…1. Зафиксировать указанные в п. 3 характеристики. Определить эквивалентную передаточную функцию замкнутой САУ по ошибке. Определить условие ликвидации скоростной ошибки.
7. Провести сравнительный анализ исходной и скорректированной различными способами САУ.
Контрольные вопросы
1. Какие вам известны способы включения корректирующих устройств в САУ?
2. Как осуществляется переход от корректирующих устройств одного типа к другому?
3. Каким образом вводятся интегралы и производные в САУ?
4. Как изодромные устройства влияют на динамические свойства САУ?
5. Как влияет регулирование по производным от ошибки на динамические показатели САУ в различных режимах регулирования?
6. Какие существуют виды обратных связей?
7. Как влияют обратные связи на показатели качества САУ?
8. Как выполнить расчет эквивалентной обратной связи?
9. Что такое комбинированное управление в САУ?
10. Как изменяется точность САУ при введении регулирования по управляющему и возмущающему воздействиям?
Лабораторная работа № 7.
