ПОТОЧНІ КОНТРОЛЬНІ РОБОТИ
З
НАВЧАЛЬНОЇ ДИСЦИПЛІНИ
«ОСНОВИ ВИЩОЇ МАТЕМАТИКИ»
СПЕЦІАЛЬНОСТІ: 5.05150101 «Друкарське виробництво»
Урок № 13. Контрольна робота № 1. 
Модуль 1. «Комплексні числа».
Модуль 2. «Лінійна алгебра».
Теми: «Комплексні числа і дії над ними»,
«Форми запису комплексних чисел».
«Елементи теорії матриць»,
«Загальна теорія СЛАР».
Завдання 1. Для комплексних чисел  та
та 
 :
:
а) знайти модуль та головне значення;
б) записати їх в тригонометричній та показникові формах;
в) обчислити суму, різницю, добуток та частку комплексних
чисел  та
та 
 .
.
1. 


 .
.
2. 


 .
.
3. 
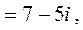

 .
.
4. 


 .
.
5. 
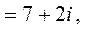

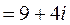 .
.
6. 


 .
.
Завдання 2. Розв’язати рівняння:
1. 
2. 
3. 
4. 
5. 
6. 
Завдання 3. Піднести до степеня:
1.  ;
;  ; 4.
; 4.  ;
;  ;
;
2.  ;
; 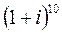 ; 5.
; 5.  ;
;  ;
;
3. 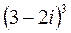 ;
;  ; 6.
; 6.  ;
; 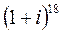 .
.
Завдання 4. Обчислити визначники матриць:
1. а) 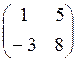 б)
б) 
2. а)  б)
б) 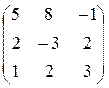
3. а)  б)
б) 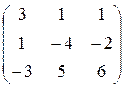
4. а) 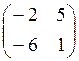 б)
б) 
5. а) 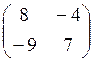 б)
б) 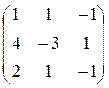
6. а) 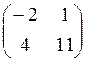 б)
б) 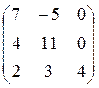
Завдання 5. Розв’язати систему лінійних рівнянь методом Крамера:
1.  2.
2. 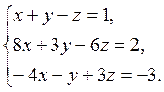
3. 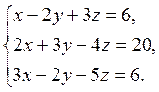 4.
4. 
5. 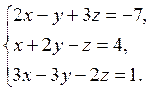 6.
6. 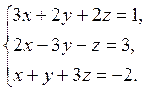
Урок № 20. Контрольна робота № 2.

Модуль 3. «Аналітична геометрія на площині».
Теми: «Лінії на площині», «Криві другого порядку».
Завдання 1. Відомі вершини трикутника АВС. Знайти:
а) рівняння сторони АВ;
б) кут В трикутника АВС.
Виконати рисунок.
1. А(8, 6), В(6, 4), С(-2, 14).
2. А(4, 6), В(2, 2), С(-1, 3).
3. А(-6, -2), В(-3, 1), С(1, -4).
4. А(-1, -1), В(1, 3), С(5, -2).
5. А(-8, 4), В(-2, 1), С(1, -3).
6. А(2, -5), В(1, -3), С(4, 1).
Завдання 2. Привести задане рівняння еліпса до канонічного вигляду і обчислити його осі. Виконати рисунок.
1. 4х2+9у2=36; 4. 16х2+4у2=64;
2. 25х2+4у2=100; 5. 4х2+36у2=144;
3. 9х2+25у2=225; 6. 49х2+9у2=441;
Завдання 3. Обчислити координати фокусів і ексцентриситет заданої гіперболи. Виконати рисунок.
1.  4.
4. 
2.  5.
5. 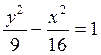
3.  6.
6. 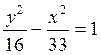
Завдання 5. Знайти фокус і директрису для заданої параболи. Виконати рисунок.
1.  4.
4. 
2. 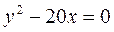 5.
5. 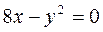
3. 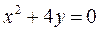 6.
6. 
Урок № 34. Контрольна робота № 3.

Модуль 4. «Диференціальне числення функцій».
Теми: «Диференційованість функції однієї змінної», «Основні теореми диференціального числення», «Схема дослідження функції і побудова її графіка», «Диференційованість функцій багатьох змінних», «Дослідження функцій багатьох змінних на екстремум, умовний екстремум».
Завдання 1. Знайти похідні функцій: а) складної функції; б) неявної функції; в) параметрично заданої функції; г) використовуючи логарифмічне диференціювання.
1. а)  ; б)
; б) 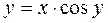 ;
;
в) 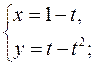 г)
г)  .
.
2. а) 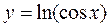 ; б)
; б) 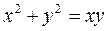 ;
;
в)  г)
г) 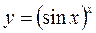 .
.
3. а) 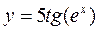 ; б)
; б)  ; в)
; в) 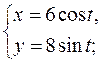 г)
г) 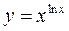 .
.
4. а) 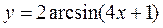 ; б)
; б)  ;
;
в)  г)
г) 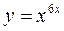 .
.
5. а)  б)
б)  ;
;
в) 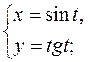 г)
г) 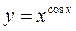 .
.
6. а) 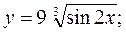 б)
б) 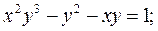
в)  г)
г) 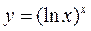 .
.
Завдання 2. Знайти найбільше та найменше значення функції на заданому проміжку:
1) 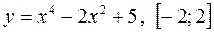 ; 4)
; 4) 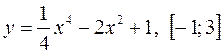 ;
;
2)  ; 5)
; 5)  ;
;
3)  ; 6)
; 6) 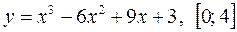
Завдання 3. Знайти всі похідні другого порядку для заданих функцій:
1.  ; 4.
; 4. 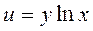 ;
;
2.  ; 5.
; 5.  ;
;
3. 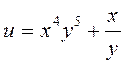 ; 6.
; 6. 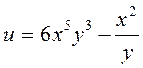 .
.
Завдання 4. Довести, що задана функція  z задовольняє задане
z задовольняє задане
рівняння:
1. 
2. 
3. 
4. 
5. 
6. 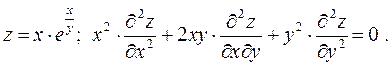
Завдання 5. Дослідити задану функцію на екстремум.
1.  ; 4.
; 4.  ;
;
2. 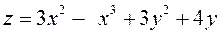 ; 5.
; 5.  ;
;
3. 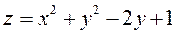 ; 6.
; 6.  .
.
Урок № 46. Контрольна робота № 4.
Модуль 5. «Інтегральне числення функцій».
Теми: «Невизначений інтеграл»,
«Визначений інтеграл», «Застосування визначених інтегралів».
Завдання 1. Знайти невизначені інтеграли. Результат перевірити диференціюванням:
1. а)  б)
б) 
2. а)  б)
б)  ;
;
3. а)  б)
б) 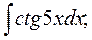
4. а) 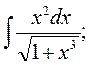 б)
б) 
5. а) 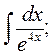
 б)
б)  6. а)
6. а) 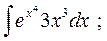 б)
б) 
Завдання 2. Обчислити визначені інтеграли:
1. а) 
 ; б)
; б) 
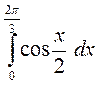 ; 2. а)
; 2. а) 
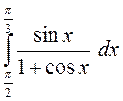 ; б)
; б) 
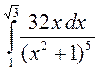 ; 3. а)
; 3. а) 
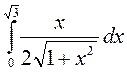 ; б)
; б)  ; 4. а)
; 4. а) 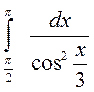 ; б)
; б)  ;
;
5. а)  ; б)
; б) 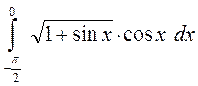 ;
;
6. а) 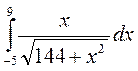 ; б)
; б) 
 ;
;
Завдання 3. Обчислити площу фігури, обмеженої графіками функцій:
1. 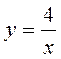 ;
;  ;
;  ;
;
2.  ;
;  ;
;
3. 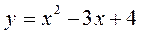 ;
; 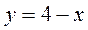 ;
;
4.  ;
;  ;
; 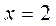 ;
;
5.  ;
;  ;
;
6.  ;
;  .
.
Урок № 55. Контрольна робота № 5.
Модуль 6. «Диференціальні рівняння».
Теми: «Диференціальні рівняння 1-го порядку»,
«Диференціальні рівняння 2-го порядку, що
дозволяють знизити порядок»,
«Лінійні диференціальні рівняння 2-го порядку».
Завдання 1. Знайти загальний розв’язок (інтеграл) диференціальних рівнянь першого порядку:
1.  2.
2. 
3.  4.
4. 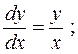
5.  6.
6. 
Завдання 2. Знайти загальний розв’язок (інтеграл) диференціальних рівнянь другого порядку:
1.  ; 2.
; 2. 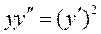 ;
;
3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  .
.
Завдання 3. Знайти загальний розв’язок (інтеграл) лінійних диференціальних рівнянь другого порядку:
1.  ; 2.
; 2.  ;
;
3. 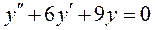 ; 4.
; 4.  ;
;
5.  ; 6.
; 6. 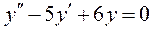 .
.






