Рассмотрим систему сил  ,
,  ,
,  ,
,  ,
,  , приложенных в точке А (рис. 5, а). Требуется найти их равнодействующую.
, приложенных в точке А (рис. 5, а). Требуется найти их равнодействующую.
Применив правило силового треугольника, сложим силы  и
и  . Для этого из конца вектора
. Для этого из конца вектора  =
=  отложим вектор
отложим вектор  =
=  и, соединив точки А и С, получим геометрическую сумму (равнодействующую) сил
и, соединив точки А и С, получим геометрическую сумму (равнодействующую) сил  и
и  :
:

 .
.
Теперь сложим силу  с силой
с силой  . Для этого из конца вектора
. Для этого из конца вектора  =
=  отложим вектор
отложим вектор  =
=  и, соединив точки А и D, получим равнодействующую трех сил:
и, соединив точки А и D, получим равнодействующую трех сил:

 .
.
Далее, отложив  =
=  и,соединив точки А и Е, получимравнодействующую четырех сил:
и,соединив точки А и Е, получимравнодействующую четырех сил: 

 .
.
Наконец, отложив 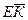 =
=  и соединив точки А и К, получим искомую равнодействующую:
и соединив точки А и К, получим искомую равнодействующую:

 .
.
Из рис.5, а видим, что для получения этого окончательного результата не обязательно определять промежуточные равнодействующие  ,
,  т. д., а достаточно из конца вектора
т. д., а достаточно из конца вектора  =
=  , , отложить вектор
, , отложить вектор  =
=  , из конца вектора
, из конца вектора  отложить вектор
отложить вектор  =
=  и т. д., а затем «замкнуть» получившийся силовой многоугольник вектором
и т. д., а затем «замкнуть» получившийся силовой многоугольник вектором  . При этом вектор равнодействующей
. При этом вектор равнодействующей  исходит из начала первой силы и заканчивается в конце последней силы.
исходит из начала первой силы и заканчивается в конце последней силы.
Заметим, что порядок построения сторон силового многоугольника АВСДЕК (рис.5, а) не влияет на окончательный результат. Например, на рис. 5, б силовой многоугольник AB1ClD1E1K1 замыкается вектором  =
=  , хотя порядок сложения векторов здесь иной:
, хотя порядок сложения векторов здесь иной:
 =
= 

 .
.
Определение равнодействующей системы сходящихся сил—необходимый этап для решения задачи уравновешивания заданной системы. Чтобы уравновесить систему сил, достаточно к ней добавить еще одну силу, численно равную равнодействующей, но направленную в противоположную сторону. Например, требуется уравновесить систему пяти сил (рис. 5, а). Для этого, построив силовой многоугольник ABCDEK, вдоль линии ак добавим силу  ,
,
численно равную равнодействующей  но противоположно направленную (рис. 5, в). Образовавшаяся система сходящихся сил
но противоположно направленную (рис. 5, в). Образовавшаяся система сходящихся сил  ,
,  ,
,  ,
,  ,
,  ,
,  уравновешена. В такой уравновешенной системе любая из сил оказывается уравновешивающей по отношению к остальным.
уравновешена. В такой уравновешенной системе любая из сил оказывается уравновешивающей по отношению к остальным.
Таким образом, если построить силовой многоугольник уравновешенной системы сил (рис.5, в), то он получится замкнутым, т. е. замыкающий вектор  = 0, так как конец последнего слагаемого вектора совпадает с началом первого.
= 0, так как конец последнего слагаемого вектора совпадает с началом первого.

Рис. 5. Сложение плоской системы сходящихся сил.
Следовательно, замкнутый силовой многоугольник выражает в геометрической форме необходимое и достаточное условие равновесия системы сходящихся сил: система сходящихся сил уравновешена тогда и только тогда, когда силовой многоугольник замкнут.
Геометрическое условие равновесия (замкнутый силовой многоугольник) широко используется при решении задач статики.
1.9. Определение равнодействующей системы






