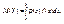Корреляционным моментом системы двух случайных величин называется второй смешанный центральный момент: Kxy = μ1,1 = M ((X – M (X))(Y – M (Y))).Для дискретных случайных величин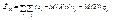 
для непрерывных случайных величин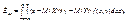 
Безразмерной характеристикой коррелированности двух случайных величин является коэффи-циент корреляции 
. Корреляционный момент описывает связь между составляющими двумерной случайной вели-чины. Действительно, убедимся, что для независимых Х и Y Kxy = 0. В этом случае f (x,y) = =f 1(x) f 2(y), тогда 
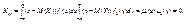Итак, две независимые случайные величины являются и некоррелированными. Однако понятия коррелированности и зависимости не эквивалентны, а именно, величины могут быть зависимы-ми, но при этом некоррелированными. Дело в том, что коэффициент корреляции характеризует не всякую зависимость, а только линейную. В частности, если Y = aX + b, то rxy = ±1. Найдем возможные значения коэффициента корреляции. Теорема 9.1. 
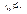Доказательство. Докажем сначала, что 
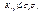Действительно, если рассмотреть случай-ную величину 
и найти ее дисперсию, то получим: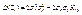 
. Так как дисперсия всегда неотрицательна, то 
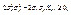откуда 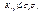Отсюда 
что и требовалось доказать.
20. Случайные функции. Понятие случайной функции. Математическое ожидание случайной функции. Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргу-мента Х: Y = φ (X). Выясним, как найти закон распределения функции по известному закону распределения аргумента.1) Пусть аргумент Х – дискретная случайная величина, причем различным значениям Х соот-ветствуют различные значения Y. Тогда вероятности соответствующих значений Х и Y равны. 2) Если разным значениям Х могут соответствовать одинаковые значения Y, то вероятности значений аргумента, при которых функция принимает одно и то же значение, складываются.
3) Если Х – непрерывная случайная величина, Y = φ (X), φ (x) – монотонная и дифференцируемая функция, а ψ (у) – функция, обратная к φ (х), то плотность распределения g (y) случайно функции Y равна: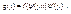 
Математическое ожидание функции одного случайного аргумента.
Пусть Y = φ (X) – функция случайного аргумента Х, и требуется найти ее математическое ожидание, зная закон распределения Х.
1)Если Х – дискретная случайная величина, то
(10.2)
2)Если Х – непрерывная случайная величина, то M (Y) можно искать по-разному. Если известна плотность распределения g (y), то
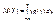
Если же g (y) найти сложно, то можно использовать известную плотность распределения f (x):
В частности, если все значения Х принадлежат промежутку (а, b), то
