Для нахождения критических напряжений 
надо вычислить критическую силу 
, т. е. наименьшую осевую сжимающую силу, способную удержать в равновесии слегка искривленный сжатый стержень.
Эту задачу впервые решил академик Петербургской Академии наук Л. Эйлер в 1744 году.
Заметим, что самая постановка задачи иная, чем во всех ранее рассмотренных отделах курса. Если раньше мы определяли деформацию стержня при заданных внешних нагрузках, то здесь ставится обратная задача: задавшись искривлением оси сжатого стержня, следует определить, при каком значении осевой сжимающей силы Р такое искривление возможно.
Рассмотрим прямой стержень постоянного сечения, шарнирно опертый по концам; одна из опор допускает возможность продольного перемещения соответствующего конца стержня (рис.3). Собственным весом стержня пренебрегаем.
Рис.3. Расчетная схема в «задаче Эйлера»
Нагрузим стержень центрально приложенными продольными сжимающими силами 
и дадим ему весьма небольшое искривление в плоскости наименьшей жесткости; стержень удерживается в искривленном состоянии, что возможно, так как .
Деформация изгиба стержня предположена весьма малой, поэтому для решения поставленной задачи можно воспользоваться приближенным дифференциальным уравнением изогнутой оси стержня. Выбрав начало координат в точке А и направление координатных осей, как показано на рис.3, имеем:
| (1) |
Возьмем сечение на расстоянии х от начала координат; ордината изогнутой оси в этом сечении будет у, а изгибающий момент равен
По исходной схеме изгибающий момент получается отрицательным, ординаты же при выбранном направлении оси у оказываются положительными. (Если бы стержень искривился выпуклостью книзу, то момент был бы положительным, а у — отрицательным и .)
Приведенное только что дифференциальное уравнение принимает вид:
деля обе части уравнения на EJ и обозначая дробь 
через 
приводим его к виду:
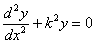
Общий интеграл этого уравнения имеет вид:
Это решение заключает в себе три неизвестных: постоянные интегрирования а и b и значение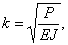 
, так как величина критической силы нам неизвестна.
Краевые условия на концах стержня дают два уравнения:
в точке А при х = 0 прогиб у = 0,
В х = 1 у = 0.
Из первого условия следует (так как 
и cos kx =1)
0 = b.
Таким образом, изогнутая ось является синусоидой с уравнением
| (2) |
Применяя второе условие, подставляем в это уравнение
у = 0 и х = l
получаем:
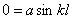
Отсюда следует, что или а или kl равны нулю.
Если а равно нулю, то из уравнения (2) следует, что прогиб в любом сечении стержня равен нулю, т. е. стержень остался прямым. Это противоречит исходным предпосылкам нашего вывода. Следовательно, sin kl = 0, и величина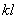 
может иметь следующий бесконечный ряд значений:
где 
— любое целое число.
Отсюда 
, а так как 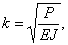то
и 
Иначе говоря, нагрузка, способная удержать слегка искривленный стержень в равновесии, теоретически может иметь целый ряд значений. Но так как отыскивается, и интересно с практической точки зрения, наименьшее значение осевой сжимающей силы, при которой становится возможным продольный изгиб, то следует принять 
.
Первый корень =0 требует, чтобы было равно нулю, что не отвечает исходным данным задачи; поэтому этот корень должен быть отброшен и наименьшим корнем принимается значение 
. Тогда получаем выражение для критической силы:
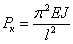
| (3) |
(Здесь J —минимальный момент инерции поперечного сечения стержня.) Это — так называемая формула Эйлера для сжатого стержня с шарнирно-опертыми концами. Значению критической силы (3) соответствует изгиб стержня по синусоиде с одной полуволной [формула (2)]
Лекция № 43. Анализ формулы Эйлера
Значениям критической силы высших порядков соответствуют искривления по синусоидам с двумя, тремя и т. д. полуволнами (Рис.1):
| (1) |
Таким образом, чем больше точек перегиба будет иметь синусоидально-искривленная ось стержня, тем большей должна быть критическая сила. Более полные исследования показывают, что формы равновесия, определяемые формулами (1), неустойчивы; они переходят в устойчивые формы лишь при наличии промежуточных опор в точках В и С (рис.1).
Рис.1
Таким образом, поставленная задача решена; для нашего стержня наименьшая критическая сила определяется формулой
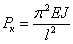
а изогнутая ось представляет синусоиду
Величина постоянной интегрирования а осталась неопределенной; физическое значение ее выяснится, если в уравнении синусоиды положить 
; тогда 
(т. е. посредине длины стержня) получит значение:
Значит, а — это прогиб стержня в сечении посредине его длины. Так как при критическом значении силы Р равновесие изогнутого стержня возможно при различных отклонениях его от прямолинейной формы, лишь бы эти отклонения были малыми, то естественно, что прогиб f остался неопределенным.
Он должен быть при этом настолько малым, чтобы мы имели право применять приближенное дифференциальное уравнение изогнутой оси, т. е. чтобы 
было по прежнему мало по сравнению с единицей.
Получив значение критической силы, мы можем сейчас же найти и величину критического напряжения , разделив силу на площадь сечения стержня F; так как величина критической силы определялась из рассмотрения деформаций стержня, на которых местные ослабления площади сечения сказываются крайне слабо, то в формулу для входит момент инерции 
поэтому принято при вычислении критических напряжений, а также при составлении условия устойчивости вводить в расчет полную, а не ослабленную, площадь поперечного сечения стержня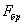 
. Тогда
Таким образом, критическое напряжение для стержней данного материала обратно пропорционально квадрату отношения длины стержня к наименьшему радиусу инерции его поперечного сечения. Это отношение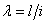 
называется гибкостью стержня и играет весьма важную роль во всех проверках сжатых стержней на устойчивость.
Из последнего выражения видно видно, что критическое напряжение при тонких и длинных стержнях может быть весьма малым, ниже основного допускаемого напряжения на прочность 
. Так, для стали 3 с пределом прочности 
допускаемое напряжение может быть принято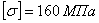 
; критическое же напряжение для стержня с гибкостью 
при модуле упругости материала 
будет равно
Таким образом, если бы площадь сжатого стержня с такой гибкостью была подобрана лишь по условию прочности, то стержень разрушился бы от потери устойчивости прямолинейной формы.
