Время одного из устройств описывается произвольной функцией распределения (например ОП), а время другого - экспоненциальным законом (ЦП). Если наблюдать за системой в любой момент времени t, то время выборки команды из ОП зависит от того, сколько она этим уже занималась. Существует прием, который позволяет решать такие системы, который заключается в том, что мы наблюдаем за системой не в любой малый интервал времени (Dt), а в «специальный». В качестве «специального» будем считать время, непосредственно перед появлением команды из ОП. Для описания системы введем вероятность Рi - вероятность того, что в БП+ЦП находиться i команд в момент времени перед появлением очередной из ОП и qi - вероятность того, что за время выборки одной команды ОП ЦП выполнит ровно i команд. Следовательно поведение системы может быть описано с помощью матрицы переходных вероятностей.
Номер столбца - состояние системы после завершения работы ОП и номер строки - состояние системы до появления команды из ОП. Предположим система находится в состоянии 0. Из этого состояния можно попасть только в состояние 0 или 1 с вероятностями 1-q0 и q0 соответственно. Если система находиться в состоянии 1, то из него она может попасть в состояние или 0, или 1 или 2 с вероятностями 1-q0-q1 и q1 и q0 соответственно и т.д.
При i=n+1 команда, которая должна быть считана из ОП не может поступить в БП, следовательно происходит блокировка работы ОП, при этом сама команда останется в ОП. После выполнения одной команды ЦП, система перейдет в состояние n, следовательно к таблице надо приписать еще одну строку: 
Время блокировки равно времени выполнения, которое осталось для обслуживания команды в ЦП. Время пребывания системы в i-ом (i=0,1,2,...,n) равно времени выполнения одной команды ОП. Время пребывания системы в состоянии n+1 равно времени выполнения одной команды ОП плюс одной команды в ЦП.
Среднее время выполнения одной команды системой:
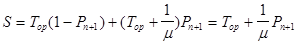, где ТОР - среднее время выборки одной команды ОП, а 1/m - среднее время выполнения одной команды в ЦП.
Необходимо определить Рn+1, если qi известны. Для этого решим систему:
В этой системе одно уравнение линейно зависимо, следовательно надо отбросить любое уравнение и добавить уравнение нормировки.
Лекция №9.
Необходимо вычислить qi. Время выборки команды из ОП является случайной величиной, подчиняющейся произвольной функции распределения F(t). Пусть время выборки одной команды равно t. Разобьем это время на m одинаковых интервалов по Dt (Dt*m=t). Вероятность того, что за время Dt будет выполнена ровно одна команда в условиях экспоненциального закона распределения, равна: 
. Вероятность того, что за время t выполнится ровно i команд, равна:
