 |
Имеется тракт ОП-ЦП. ЦП вырабатывает адрес обращения, по которому происходит считывание команды. Во время считывания работает ОП, а ЦП простаивает. Пусть команда будет с непосредственной адресацией, следовательно во время ее выполнения в ЦП ОП будет простаивать. Производительность была бы выше, если бы ЦП постоянно выполняла бы команды, для этого нужно при выполнении очередной команды прочитать следующую, которую мы поместим в специальный буфер команд. Естественно, когда команда поступает из БП в ЦП, она затирается в БП. БП служит согласующим звеном между ОП и ЦП. Если время выполнения одной команды в ЦП меньше либо равна времени выборки команды из ОП, тогда БП не нужна. Но в действительности эти времена не постоянны.
Пусть время выполнения одной команды в ЦП изменяется от minTоп до maxTоп, время выборки команды из ОП лежит в диапазоне от minTцп до maxTцп. Для простоты будем считать, что передача информации из ОП в ЦП через БП происходит за нулевое время. И емкость буфера равна n.
Определим Топ и Тцп как
ì t1 c вероятностью p1
Топ = ít2 c вероятностью p2 (*)
ê.................................... 
îtk c вероятностью pk
ìt1 c вероятностью q1
Тцп = ít2 c вероятностью q2 (**)
ê....................................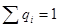 
îtk c вероятностью qk
Нас интересует производительность системы, то есть появление команд на выходе.
Пусть S - среднее время выполнение команды этой системой.
цп = 
- среднее время выполнения одной команды в ЦП. оп = 
- среднее время выборки одной команды из ОП. Рцп - вероятность простоя ЦП. Рцп - вероятность простоя ОП. Тогда 
.
Так как БП имеет ограниченную емкость, то если в момент поступления команды из ОП в БП, последняя полностью заполнена, то возникает проблема. Существует два решения этой проблемы: 1) команда теряется и будет происходит считывание с тем же адресом обращения до тех пор пока ЦП не обработает очередную команду и следующая команда поступит на обработку из БП. 2) Считанная команда остается на внутренних регистрах ОП и при этом происходит блокировка работы памяти. Будем считать, что у нас вторая дисциплина.
Рассмотрим тракт ОП-БП-ЦП, в котором время работы устройств подчинены различным законам распределения.
Дискретное распределение.
Определим состояние системы тремя параметрами U1U2U3, где U1 - указывает сколько времени осталось до завершения считывания команды из ОП; U2 - количество команд в буфере; U3 - указывает сколько времени осталось до завершения выполнения команды в процессоре.
Построим граф переходов данной системы.
Граф переходов содержит 6(n+1) состояний. Найдем 
- вероятность пребывания в состоянии 
. Для этого составим систему уравнений. Уравнение для некоторой вершины графа в левой части содержат , а в правой части - сумму произведений пометок дуг, входящих в выбранную вершину, на вероятности с пометками вершин, из которых эти дуги исходят.
ДЗ. Выписать все уравнения и определить вероятности простоя как ЦП, так и ОП.
Лекция №6.
