Экспоненциальное распределение.

 

Экспоненциальное распределение является непрерывным распределением и является приближением геометрического распределения, т.к. при стремлении такта к 0 геометрическое распределение стремиться к экспоненциальному.

Определение: - вероятность того, что выполнение команды завершится к моменту времени t.

Для экспоненциального закона распределения .

		t

 

Дополнении к функции распределения: 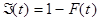- вероятность того, что выполнении команды не закончиться к моменту t.

Плотность вероятности:

ДЗ. Просмотреть свойства экспоненциального закона распределения. Математическое ожидание, дисперсия, первый и второй моменты.

Рассмотрим такую модель:

 

Поскольку время выполнения команды не зависит от того сколько данная команда выполнялась до этого нет необходимости вводить параметр, который будет содержать информацию о том сколько времени уже выполняется команда в процессоре, или в памяти, или одновременно и там и там, следовательно достаточно указать сколько находиться команд в системе (от 0 до n+1). Рассмотрим состоянии системы в некоторый момент времени t. Введем Р_i(t) - вероятность того, что в момент наблюдения t в системе находится ровно i команд. При i=0,1,...,n+1 ОП не может быть заблокировано. Введем n+2 состояние и будем считать, что в этом состоянии ОП заблокировано.

Найдем Р_i(t). Для этого рассмотрим малый интервал времени Dt и пусть в момент t+Dt система находиться в состоянии i. Найдем вероятность P_i(t+Dt) для всех значениях i. В момент времени t система могла находиться в любом состоянии. Посмотрим как можно из состояния системы в момент времени t попасть в состояние i в момент времени t+Dt.

1) 0<i<n+2

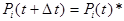вероятность того, что ни ОП, ни ЦП не завершит обработку команды или оба устройства выполнят одно и тоже число команд.

Определим вероятность того, что за Dt ни ОП, ни ЦП не завершит обработку команды:

ДЗ. Разложение е^х.

Символ О(Dt) означает величины, для которых справедливо O(Dt)/ Dt ®0 при Dt®¥. Вероятность того, что за Dt устройствами будет выполнено ровно по к команд равняется О(Dt).

Действительно: .

Поэтому:

+ вероятность того, что за время Dt 1) ЦП выполнит 1 команду, а ОП - 0 команд, либо 2) ЦП выполнит на 1 команду больше чем ОП.

Определим вероятность первого события: .

Вероятность второго события равна О(Dt). Следовательно:

+

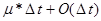
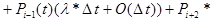вероятность того, что 1) ЦП выполнит 2 команды, а ОП ни одной, либо 2) ЦП выполнит на 2 команды больше, чем в ОП.

Определим вероятность первого события: .

Вероятность второго события равна О(Dt). Отсюда вероятность попадания в состояние i из состояния i+2 равна О(Dt), аналогично и из состояния i-2. Следовательно и из состояний i±3, i±4,...,i±k вероятность попадания в состояние i равна О(Dt).

Мы получили формулу полной вероятности того, что система окажется в момент времени t+Dt в состоянии i (0<i<n+2):

+

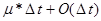
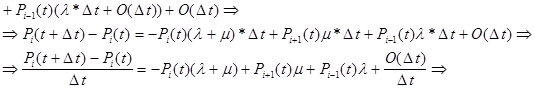
(возьмем предел каждой части равенства при Dt®¥)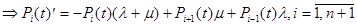

 

Лекция №8

 

Мы получили систему дифференциальных уравнений первого порядка:

(1)

(2)

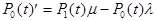(3)

Одно из этих уравнений необходимо отбросить и добавить уравнение нормировки:

Эта система уравнений позволяет описать переходный процесс во времени. Для этого нужно задать состояние системы в нулевой момент времени. Пусть

 

 

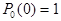
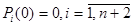
Изменить

 

 

Если наблюдать за системой достаточно долго, то можно говорить о некотором стационарном поведении системы. Решается эта система достаточно сложно. Стационарные характеристики такой системы получаются достаточно легко: для n<¥ этот предел всегда существует, если же n®¥, то предел не всегда существует. Пусть , тогда взяв предел от левой и правой части каждого уравнения системы получим:

Следовательно:

(1*)

(2*)

(3*)

Решим получившуюся систему уравнений. Из (3*) => . Решаем (1*) и (3*) при i=1:

Отсюда следует:

ДЗ. Пусть l=m. Чему равняется вероятность пребывания в том либо в другом состоянии? Чему равно среднее время выполнения команды этой системой.

Пусть n=¥. Чему равны Р_i при 1) l=m 2) l<m 3) l>m? Чему равно среднее число команд в системе при n<¥?

 

Вложенные цепи Маркова.