Для поддержания в цепи постоянного тока проводимости необходимо, чтобы на носителя заряда действовали не только кулоновские силы, но также ещё и иные, не электростатические (сторонние) силы. Под действием сторонних сил носители заряда движутся внутри источника электрической энергии против сил электростатического поля, так что на концах внешней части цепи поддерживается постоянная разность потенциалов.
Для стационарных токов (сила тока не изменяется с течением времени) справедливо следующее.
Сила тока через замкнутую поверхность равна нулю:
.
Данное соотношение является условием стационарности электрического тока и математической формулировкой закона сохранения электрического заряда.
В электрической цепи справедлив закон Ома, определяющий плотность электрического тока (в дифференциальной форме) или силу тока (в интегральной форме).
В произвольной точке участка электрической цепи, содержащей источник электрической энергии (неоднородный участок), существует электростатическое поле кулоновских сил с напряжённостью 
кул. и поле сторонних сил с напряжённостью стор.=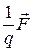 
стор..
Закон Ома (дифференциальная форма)
Плотность электрического тока пропорциональна результирующей напряженности поля кулоновских и сторонних сил:
( кул.+ стор.),
где r – удельное сопротивление проводника.
Для большинства металлических проводников удельное сопротивление зависит от температуры по линейному закону
,
где a – температурный коэффициент сопротивления, град-1, rо – удельное сопротивление при температуре 0оС, tо – температура проводника, оС.
Разность потенциалов на участке электрической цепи численно равна работе, которую совершают кулоновские силы при перемещении положительного единичного заряда по участку цепи из точки 1 в точку 2:
кул× d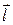 
=(j1 - j2).
Электродвижущая сила источника тока (ЭДС) e12 равна работе, совершаемой сторонними силами при перемещении положительного единичного заряда по участку цепи из точки 1 в точку 2:
стор.× d .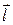
Напряжением U12 называется физическая величина, численно равная работе, совершаемой результирующим полем кулоновских и сторонних сил при перемещении вдоль цепи из точки 1 в точку 2 положительного единичного заряда:
кул. + стор.)× d =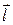 
.
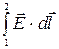Сопротивлением R12 участка цепи между точками 1 и 2 называется интеграл
,
где S – сечение проводника в месте расположения элемента проводника dl.
Если r = const и S = const, то
,
где l 12 – длина проводника между точками 1 и 2.
Закон Ома (интегральная форма) для неоднородного участка цепи
Сила электрического тока пропорциональна напряжению на участке цепи и обратно пропорциональна его сопротивлению:
.
Закон Ома для замкнутой электрической цепи
,
где e – алгебраическая сумма всех ЭДС, приложенных в цепи; R – эквивалентное внешнее (по отношению к ЭДС) сопротивление; r – эквивалентное сопротивление всех ЭДС.
При прохождении электрического тока по проводникам они нагреваются. Закон Джоуля – Ленца (интегральная форма)
Количество теплоты dQ, выделяющееся в проводнике за малое время dt, пропорционально квадрату силы тока I, электрическому сопротивлению R проводника и промежутку времени:
dQ = I2Rdt = (IU)dt = (U 2/ R)dt,
где U = IR – напряжение на проводнике.
Количество тепла, выделяющееся в проводнике за конечный промежуток времени (от t1 до t2):
,
если I = const, то Q = I 2R (t2 - t1).
Дифференциальная форма закона Джоуля – Ленца
Плотность тепловой мощности (удельная тепловая мощность) пропорциональна квадрату плотности тока и удельному сопротивлению:
.
1.14. Правила Кирхгофа
Первое правило Кирхгофа (правило узлов ) –алгебраическая сумма токов, сходящихся в узле, равна нулю:
,
где n – число проводников, сходящихся в узле, I k – ток в k-ом проводнике (рис. 1.8).
Положительными считаются токи, подходящие к узлу (токи I1, I3), отрицательными – токи, отходящие от узла (токи I2, I4, I5), или наоборот.
Второе правило Кирхгофа (правило контуров) – в любом замкнутом контуре, произвольно выбранном в разветвлённой электрической цепи, алгебраическая сумма напряжений на соответствующих участках этого контура равна алгебраической сумме ЭДС в контуре:
.
Для применения второго правила Кирхгофа выбирается определённое направление обхода контура (по часовой стрелке или против неё). Положительными считаются токи, направления которых совпадает с направлением обхода контура. ЭДС источников считаются положительными, если они создают токи, совпадающие по направлению с направлением обхода контура.
Примеры решения задач
1. 
Прямая бесконечная нить, равномерно заряженная электричеством с линейной плотностью t1 =3×10-7 Кл/м, и отрезок длиной l =20 см, равномерно заряженный электричеством с линейной плотностью t2 =2×10-7 Кл/м, расположены в одной плоскости перпендикулярно друг к другу на расстоянии r0 = 10 см. Определить силу взаимодействия между ними.
Решение
В задаче рассматривается взаимодействие распределённых зарядов, поэтому для нахождения силы F следует воспользоваться соотношением:
. (1)
Нить создаёт вокруг себя электростатическое поле, в котором находится заряд, распределённый на отрезке длины l. Если выделить на этом отрезке малый участок длиной dr, то находящийся на нём заряд
dq = t2dr (2)
можно считать точечным и рассматривать dF как силу, действующую со стороны электрического поля нити на dq. – вектор напряжённости поля нити в месте нахождения электрического заряда dq. Электрическое поле равномерно заряженной нити определяется выражением
. (3)
Выражение (1) можно переписать в скалярной форме, учитывая, что векторы и 
параллельны:
dF = Edq. (4)
Подставив (2) и (3) в (4), получим
. (5)
Для нахождения результирующей силы, действующей на отрезок нити с зарядом q2 со стороны поля прямой бесконечной нити, проинтегрируем выражение (5) в пределах от r0 до (r0+l):
. (6)
После подстановки числовых значений получим
.
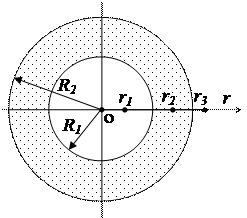
2. Полый стеклянный шар несёт равномерно распределённый по объёму заряд. Его объёмная плотность r =100 нКл/м3. Внутренний радиус шара R1 =5 см, а наружный R2 =10 см. Найти напряжённость электрического поля на расстоянии: а) r1 =3 см; б) r2 =6 см; в) r3 =12 см от центра шара.
Решение
Так как заряд шара распределён в пространстве симметрично относительно центра шара О, то и электрическое поле симметрично относительно этой точки. Это позволяет применить для решения задачи метод Гаусса. Из симметрии задачи следует, что вектор направлен вдоль 
и зависит только от расстояния до центра шара r. Выберем гауссову поверхность в виде сферы, переменного радиуса r с центром в точке О. Учтем, что модуль напряжённости поля шара одинаков во всех точках этой поверхности и Е n= E r. Так как шар диэлектрический, следует применить теорему Гаусса для вектора электрического смещения 
. Тогда поток вектора смещения сквозь гауссову поверхность
,
где S – площадь гауссовой поверхности, r – её радиус.
Всё пространство можно разбить на 3 области:
1) 0 < r < R1 2) R1 < r < R2 3) r > R2. Применим теорему Гаусса для каждой области.
Для области 0 < r < R1.
Величина свободного заряда, охватываемого поверхностью интегрирования в пределах первой области, равна нулю. Следовательно, поток вектора смещения также равен нулю, а так как площадь поверхности не нулевая, то смещение и напряжённость поля в пределах первой области равны нулю:
D1 = 0, Е1 = D/e0 = 0.
Для области R1 < r < R2.
Свободный заряд, охватываемый гауссовой поверхностью, может быть выражен через объём той части шара, которая попала внутрь сферы радиусом r2:
q своб = 
(r23-R13)r.
Применяя теорему Гаусса, получим
D24pr22 = 
,
E2 = 
= 
,
где e – диэлектрическая проницаемость стекла.
В/м.
Для области r > R2.
Внутрь поверхности попадёт весь заряд шара, поэтому
q своб = (4/3)p(R23 - R13),
и, применив теорему Гаусса, получим выражение
D3 4pr32 = (4/3) p (R23 - R13)r;
Е 3 = D 3/e0 = 
;
В/м.
3. Тонкий стержень согнут в полукольцо. Стержень заряжен с линейной плотностью t =133 нКл/м. Какую работу нужно совершить, чтобы перенести заряд q =6,7нКл из центра полукольца в бесконечность?
Решение
Работа, совершаемая силами электростатического поля по перемещению заряда из точки 1 в точку 2, может быть выражена по формуле А = q(j1 - j2), где j1 и j2 – потенциалы электрического поля, созданного полукольцом в центре и на бесконечности. Примем j2 =0. Тогда
А = qj1. (1)
Потенциал j1 найдём, используя принцип суперпозиции для потенциала поля, созданного непрерывно распределёнными зарядами. Для этого разобьем полукольцо на элементарные отрезки длиной dl. Заряд, находящийся на каждом из них, можно считать точечным: dq = tdl. Потенциал поля такого заряда в точке 1
.
Интегрируя полученное выражение в пределах от нуля до длины полуокружности l = pR, получим искомый потенциал:
j1= 
, 
. (2)
Подставим уравнение (2) в уравнение (1) и получим
А = qj1 = 
.
Подставим числовые значения заданных величин:
Дж.
4. Металлическому шару радиусом R сообщили заряд Q, после этого поверхность шара покрыли слоем диэлектрика толщиной h. Чему равна плотность связанных зарядов на внешней и внутренней поверхностях диэлектрика и полный наведённый заряд, если относительная диэлектрическая проницаемость диэлектрика e.
Решение
Применим теорему Гаусса для вектора . Поверхность интегрирования выберем в виде сферы с радиусом равным r и центром, совпадающим с центром металлического шара:
.
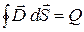Ввиду симметрии задачи интеграл в левой части
.
Сравнивая две формулы, получим выражение для модуля электрического смещения:
D = Q/4pr 2.
С другой стороны, по определению
.
Используя связь между вектором поляризации и напряженностью электрического поля, запишем
, 
,
где k – восприимчивость диэлектрика.
Подставим это выражение в формулу для электрического смещения
.
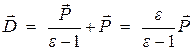Учитывая, что векторы и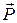 
параллельны, и используя результат применения теоремы Гаусса, запишем выражение для модуля вектора поляризации
.
Вектор 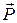перпендикулярен поверхности диэлектрика и нормальная составляющая вектора поляризации равна поверхностной плотности связанных зарядов:
P = P n = s ¢.
Тогда плотность связанных зарядов на внутренней поверхности диэлектрика рассчитывается при r=(R+0)
,
и полный заряд, наведенный на внутренней поверхности диэлектрика и связанный с s1¢ соотношением q ¢ = 4pR2s1 ¢
.
В силу закона сохранения заряда точно такой же по модулю, но противоположный по знаку заряд должен появиться на внешней поверхности диэлектрика. Очевидно, что его плотность
.
5. На два последовательно соединенных конденсатора С1 = 100 пФ и С2 = 200 пФ подано постоянное напряжение U = 300 В. Определить энергию, запасенную в каждом конденсаторе.
Решение
Так как обкладки конденсаторов соединены, то заряд, появляющийся под действием приложенного напряжения на первом конденсаторе, равен заряду, появляющемуся на втором конденсаторе (явление электростатической индукции). Поскольку заряд связан с емкостью конденсатора и напряжением на нем соотношением q = CU, то мы можем записать
C 1U 1 = C 2U 2.
С другой стороны,
U 1 + U 2 = U.
Решая совместно эту систему уравнений, найдем напряжение на первом и втором конденсаторе
,
.
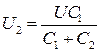Подставляя эти значения в формулу для энергии конденсатора, получим
;
.
Подставим значения величин и получим
WЭ1 = 2×10-6 Дж = 2 мкДж, WЭ2 = 1×10-6 Дж = 1 мкДж.
6. Медный проводник (удельное сопротивление меди r = 17 нОм·м) подключен к источнику с ЭДС, e = 4 В. Внутреннее сопротивление источника r = 0,1 Ом. Сечение проводника S = 0,085 мм2, длина l = 9,5 м. Считая, что ток течет по всему поперечному сечению проводника, найти величину напряженности электрического поля внутри него.
Решение
Чтобы найти напряженность электрического поля в проводнике, воспользуемся законом Ома в дифференциальной форме:
j = sE,
где j – плотность тока; E – вектор напряженности электрического поля; s – электропроводность вещества проводника, равная 1/ r.
Величина искомой напряженности электрического поля в проводнике определяется соотношением:
E = j / s = rj. (1)
Таким образом, задача нахождения напряженности поля сводится к задаче нахождения величины плотности тока j в цепи.
Плотность тока можно найти, если известна сила тока I, протекающего по проводнику
j = I / S. (2)
Полный ток в цепи найдем из закона Ома для полной цепи:
I = e / (R + r), (3)
где r – внутреннее сопротивление источника; R - сопротивление проводника.
Для R справедливо соотношение:
R = rl/S. (4)
Объединяя формулы (1) - (4), окончательно запишем
E = rj = rI / S = re / (R + r)S = re / (rl / S + r)S. (5)
Подстановка в (5) численных данных позволяет написать ответ
Е = 0,4 В/м.
7. Падение напряжения в проводнике, состоящем из двух последовательно соединенных кусков медной проволоки одинаковой длины (l 1 = l 2 = 10 м), но разного диаметра (d1 = 2d2), равно 10 В. Найти удельную тепловую мощность тока во втором куске проволоки. Удельное сопротивление меди r = 17 нОм·м.
Решение
Удельная тепловая мощность тока (плотность тепловой мощности)
w = sE 2 = 
E2 = rj 2.
Поэтому, чтобы найти w2, необходимо определить две величины: количество теплоты Q2, которое выделяется в более тонком проводнике в единицу времени, и объем этого проводника.
Количество теплоты Q2 можно найти, если учесть, что ток в проводниках один и тот же, а сопротивления проводников отличаются в 4 раза.
.
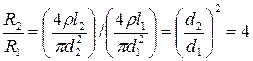Согласно закону Джоуля-Ленца, представленному в интегральной форме,
,
где Q1 – тепло, выделяющееся в единицу времени в более толстом проводнике.
Общая энергия, которая выделяется во всем проводнике, рассчитывается по формуле
, (1)
где U –падение напряжения в проводнике.
Из уравнения (1) следует, что количество теплоты, выделяющееся во втором проводнике в единицу времени,
. (2)
В уравнении (2) все величины, кроме сопротивления второго участка проводника, известны. Однако в знании R2 нет необходимости. Действительно, если связать между собой объем второго проводника с его сопротивлением
,
то нетрудно видеть, что удельная тепловая мощность тока во втором проводнике не зависит от его сопротивления
. (3)
Подставляя в соотношение (3) численные данные, получаем ответ
w 2 = 3,76×10 7 Вт/м3.
8. Заряд сферического конденсатора из-за того, что через диэлектрическую прокладку протекает ток, уменьшается за время t в n раз. Найти удельное сопротивление r прокладки, если ее диэлектрическая проницаемость равна e.
Решение
Сопротивление диэлектрика между обкладками сферического конденсатора можно найти, просуммировав сопротивления сферических слоев толщиной dr, граничащих друг с другом:
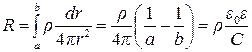, (1)
где a,b – радиусы соответственно внутренней и внешней обкладок сферического конденсатора; e0 – электрическая постоянная; C – емкость сферического конденсатора находится по формуле
.
Из уравнения (1) следует, что для определения величины удельного сопротивления материала прокладки достаточно найти произведение емкости конденсатора на полное сопротивление прокладки:
. (2)
Это можно сделать, если учесть, что за время dt конденсатор теряет заряд:
, (3)
где I – ток утечки. Знак «-» в (3) учитывает тот факт, что заряд конденсатора со временем убывает.
По закону Ома
, (4)
где U – разность потенциалов между обкладками конденсатора,
, (5)
где q – заряд конденсатора.
Объединяя формулы (3) – (5), получаем дифференциальное соотношение, в которое входит искомое произведение CR:
.
После интегрирования получаем
, (6)
где q1 – начальный заряд конденсатора; q2 – конечный.
Подставляя CRиз (6) в (2), окончательно имеем
.
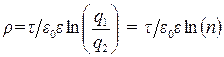Задачи для самоконтроля
1. Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распределённый по площади заряд с поверхностной плотностью s1 =1 нКл/м2 и s2 =3 нКл/м2. Определить напряжённость поля: а) между пластинами; б) вне пластин.
Ответ: а) Е1 = 
; б) Е2 =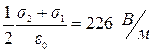 
.
2. Плоская квадратная пластинка со стороной а =10 см находится на некотором расстоянии от бесконечной равномерно заряженной (s =1 мкКл/м2) плоскости. Плоскость пластины составляет угол b =30° с линиями поля. Найти поток yD электрического смещения через эту пластинку.
Ответ: yD = 0,5 s×а2sinb = 2,5 нКл.
3. В поле, созданном заряженной сферой радиусом 10 см, движется электрон по радиусу между точками, находящимися на расстоянии 12 и 15 см от центра сферы. При этом скорость электрона изменяется от 2×105 до 2×106 м/с. Найти поверхностную плотность заряда сферы.
Ответ: 
нКл/м2 .
4. Между пластинами плоского конденсатора помещено два слоя диэлектриков – слюдяная пластина (e1 =7) толщиной d1 =1 мм и парафин (e2 =2) толщиной d2 =0,5 мм. Определить напряжённость электрических полей в слоях диэлектрика, если разность потенциалов между пластинами конденсатора U =500 В.
Ответ: Е1 = 182 кВ/м; Е2 =637 кВ/м.
5. Некоторый заряд равномерно распределен внутри шара из диэлектрика. Во сколько раз энергия электростатического поля W1, локализованная в объеме шара, меньше энергии W2, локализованной вне шара? Диэлектрическая проницаемость e =1 и в диэлектрике, и в окружающем пространстве.
Ответ: 
.
4. 6. Напряженность электрического поля в проводнике, изготовленном из материала с удельным сопротивлением r, равна E. Длина проводника l, диаметр d. Этот проводник подсоединен к источнику питания с ЭДС, равной e. Найти ток в цепи и внутреннее сопротивление источника ЭДС.
Ответ: I = 
; r = 
.
5. Падение напряжения в проводнике, состоящем из двух последовательно соединенных кусков медной и алюминиевой проволоки одинаковой длины (l 1 = l 2 = 10 м) и диаметра, равно 10 В. Найти удельную тепловую мощность тока в медной проволоке. Удельное сопротивление меди r1 = 17 нОм·м, алюминия - r2 = 25 нОм·м.
Ответ: 
= 0,96×10 7 Вт/м3 .
6. Через диэлектрическую прокладку цилиндрического конденсатора, диэлектрическая проницаемость которой равна e, протекает ток. Считая, что удельное сопротивление прокладки равно r, найти, во сколько раз уменьшится заряд конденсатора за время t.
Ответ: 
.
Контрольное задание № 3
301. Две длинные одноимённо заряженные нити расположены на расстоянии r =10 см друг от друга. Линейная плотность заряда на нитях
t1=t2 =10 мкКл/м. Найти модуль и направление вектора напряжённости результирующего электрического поля в точке, находящейся на расстоянии а =10 см от каждой нити.
302. Два точечных заряда 6,7 и 13,2 нКл находятся на расстоянии 5 см друг от друга. Найти напряженность электрического поля в точке, расположенной на расстоянии 3 см от первого заряда и 4 см - от второго.
303. Шарик, имеющий массу 0,4 г и заряд 4,9 нКл, подвешен на нити в поле плоского конденсатора, заряд которого 4,43 нКл и площадь пластин 50 см2. На какой угол от вертикали отклонится при этом нить с шариком?
304. На отрезке тонкого прямого проводника длиной l =10 см равномерно распределён заряд с линейной плотностью t =0,3 мкКл/м. Вычислить напряжённость, создаваемую этим зарядом в точке, расположенной на оси проводника и удалённой от ближайшего конца отрезка на расстояние, равное длине этого отрезка.
305. Диполь с электрическим моментом ре =10 -10 Кл×м подвешен на упругой нити. При возбуждении электрического поля напряженностью Е =3×103 В/м перпендикулярно плечу диполя и нити диполь повернулся на угол a =30о. Определить постоянную кручения нити. Постоянной кручения называют величину, равную моменту силы, который вызывает закручивание нити на один радиан.
306. Определить напряженность и потенциал поля, создаваемого точечным диполем с электрическим моментом ре =4×10 -12 Кл×м на расстоянии r =10 см от центра диполя, в направлении, составляющем угол j =60о с вектором электрического момента.
307. Тонкий стержень длиной 10 см равномерно заряжен с линейной плотностью t =1 мкКл/м. На продолжении оси стержня на расстоянии а =20 см от ближайшего его конца находится точечный заряд q =100 нКл. Определить силу взаимодействия заряженного стержня и точечного заряда.
308. Тонкое кольцо радиусом R =8 см равномерно заряжено с линейной плотностью t =10 нКл/м. Найти напряжённость электрического поля в точке, равноудалённой от всех точек кольца на расстояние r =10 см.
309. Металлический шар имеет заряд q1 =0,1 мкКл. На расстоянии, равном радиусу шара, от его поверхности находится конец нити, вытянутой вдоль силовой линии. Нить несёт равномерно распределённый по длине заряд q2 =10 нКл. Длина нити равна радиусу шара. Определить силу, действующую на нить, если радиус шара R =10 см.
310. На оси равномерно заряженного кольца радиусом R =10 см расположен стержень длиной l =20 см. Стержень равномерно заряжен с линейной плотность заряда t =10 нКл/м. Заряд кольца равен 100 нКл. Ближайший конец стержня находится в центре кольца. Найти силу взаимодействия кольца и стержня.
311. Плоская круглая пластинка радиусом r =10 см находится в воде (e =81) на некотором расстоянии от бесконечной равномерно заряженной (s =2 мкКл/м2) плоскости. Плоскость пластины составляет угол b =30° с линиями поля. Найти поток вектора напряженности через эту пластинку.
312. Электрическое поле создано бесконечной, равномерно заряженной нитью (t =0,3 мкКл/м). Определить поток вектора напряженности через прямоугольную площадку, две большие стороны которой параллельны нити и одинаково удалены от нее на расстояние r =20 см. Стороны площадки имеют размеры: а =20 см, b =40 см.
313. Металлический шар радиусом R =5 см несёт заряд q =1 нКл. Шар окружён слоем эбонита (e =2) толщиной d =2 см. Вычислить напряжённость электрического поля на расстоянии: а) r1 =3 см; б) r2 =6 см; в) r3 =9 см от центра шара.
314. Две металлические концентрические сферы имеют радиусы R1 =5 см и R2 =7 см. Заряд внутренней сферы q1 =-3,2 нКл, внешней - q2 =8,2 нКл. Найти напряжённость электрического поля на расстоянии: а) r1 =2 см; б) r2 =6 см; в) r3 =9 см от центра сфер.
315. Имеются две концентрические металлические сферы радиусами R1 =3 см и R2 =6 см. Пространство между сферами заполнено парафином (e =2). Заряд внутренней сферы q1 =-1 нКл, а внешней - q2 =2 нКл. Найти напряжённость электрического поля на расстоянии: а) r1 = 1 см; б) r2 = 5 см; в) r3 = 9 см от центра сфер.
316. На металлической сфере радиусом R =10 см находится заряд q =1 нКл. Определить напряжённость электрического поля в следующих точках: а) на расстоянии r1 =8 см от центра сферы; б) на её поверхности; в) на расстоянии r2 =15 см от центра сферы.
317. Большая плоская пластина из эбонита (e =2,6) толщиной d =1 см несет заряд, равномерно распределенный по объему с плотностью r =100 нКл/м3. Найти напряженность электрического поля вблизи центральной части пластины, вне ее и на малом расстоянии от ее поверхности.
318. Металлический шар радиусом R1, несущий заряд q =1 нКл, окружен концентрическим полым металлическим шаром с внутренним радиусом R2 и внешним R3. Заряд внешнего шара равен нулю. Построить график зависимости напряженности поля от расстояния до центра шаров. Найти потенциал шаров, если в бесконечности потенциал равен нулю.
319. Длинная бесконечная тонкостенная металлическая трубка радиусом R =2 см несёт равномерно распределённый по поверхности заряд (s =1мкКл/м2).Определить напряжённость поля в точках, отстоящих от оси трубки на расстояниях r1 =1 см и r2 =3 см.
320. Прямой металлический стержень диаметром d =5 см и длиной l =4 м несёт равномерно распределённый по поверхности заряд q =500 нКл/м. Определить напряжённость поля в точке, находящейся против середины стержня на расстоянии 1 см от его поверхности.
321. Определить потенциал в центре кольца с внешним диаметром D =0,8 м и внутренним диаметром d =0,4 м, если на нём равномерно распределён заряд q =6×10-7 Кл.
322. По тонкому кольцу радиусом R =10 см равномерно распределён заряд с линейной плотностью t =10 нКл/м. Построить график зависимости потенциала от расстояния до центра кольца и определить потенциал в точке, лежащей на оси кольца на расстоянии 5 см от центра.
323. Электрическое поле образовано положительно заряженной бесконечной нитью с линейной плотностью заряда в 2×10 -9 Кл/см. Какую скорость получит электрон под действием поля, приблизившись к нити с расстояния в 1 см до расстояния 0,5 см от нити?
324. Заряд распределён равномерно по бесконечной плоскости с поверхностной плотностью 10 нКл/м2. Определить разность потенциалов двух точек поля, одна их которых находится на плоскости, а другая удалена от плоскости на расстояние d =10 см.
325. Электрическое поле создано бесконечной равномерно заряженной плоскостью с поверхностной плотностью заряда s =2 мкКл/м2. В этом поле вдоль прямой, составляющей угол a =60° с плоскостью, из точки 1 в точку 2, расстояние между которыми Dr =20 см, перемещается точечный электрический заряд q =10 нКл, удаляясь от плоскости. Определить работу сил поля по перемещению заряда (точка 1 расположена на произвольном расстоянии от плоскости).
326. Вдоль силовой линии однородного электрического поля движется протон. В точке поля с потенциалом j1 =100 В протон имел скорость u1 =0,1 Мм/с. Определить потенциал j2 точки поля, в которой скорость протона возрастёт в n =2 раза. Отношение заряда протона к его массе q/m =96 МКл/кг.
327. Диполь с электрическим моментом ре =10-10 Кл м свободно устанавливается в однородном электрическом поле Е =1500 В/см. Вычислить работу, необходимую для того, чтобы повернуть диполь на угол j =180о.
328. Тонкий стержень длиной 10 см несёт равномерно распределённый заряд 1 нКл. Определить потенциал электрического поля в точке, лежащей на оси стержня на расстоянии 20 см от ближайшего его конца.
329. Бесконечно длинная прямая нить заряжена равномерно с линейной плотностью t =0,40 мкКл/м. Вычислить разность потенциалов точек 1 и 2, если точка 2 находится дальше от нити, чем точка 1 в n =2 раза.
330. Бесконечно длинная прямая нить заряжена равномерно с линейной плотностью t =0,01 мкКл/м. Вычислить разность потенциалов точек 1 и 2, удалённых от нити на расстояния r1 =2 см и r2 =4 см.
331. Два заряженных шарика, подвешенных на нитях одинаковой длины, опускаются в керосин плотностью 0,8 г/см3. Какова должна быть плотность материала шариков, чтобы угол расхождения нитей в воздухе и в керосине был один и тот же? Диэлектрическая проницаемость керосина e =1,6.
332. Расстояние между обкладками плоского конденсатора составляет
d =5 мм. После зарядки конденсатора до разности потенциалов U =500 В между обкладками вдвинули стеклянную пластину (e =7). Определить: 1) диэлектрическую восприимчивость стекла; 2) поверхностную плотность связанных зарядов на стеклянной пластине.
333. Расстояние между пластинами плоского конденсатора составляет
d1 =1 см, разность потенциалов U =200 В. Определить поверхностную плотность связанных зарядов эбонитовой пластины (e =3) толщиной d2 =8 мм, помещённой на нижнюю пластину конденсатора.
334. Пространство между пластинами плоского конденсатора заполнено диэлектриком с диэлектрической восприимчивостью 0,8. На пластины конденсатора подано напряжение 4 кВ. Найти поверхностную плотность зарядов на диэлектрике. Расстояние между пластинами равно 5 мм.
335. Диэлектрик поместили в электрическое поле напряжённостью
Ео =20 кВ/м. Чему равна поляризованность Р диэлектрика, если напряжённость среднего макроскопического поля в диэлектрике оказалась равной 4 кВ/м?
336. У поверхности фарфоровой пластины (e =6) напряжённость поля в вакууме 200 В/см и образует с нормалью к поверхности угол 40°. Определить: 1) угол между направлением поля и нормалью к пластине внутри пластины; 2) напряжённость поля в фарфоре.
337. Во внешнем электрическом поле напряжённостью Ео =40 МВ/м поляризованность жидкого азота Р оказалась равной 109 мкКл/м2. Определить диэлектрическую проницаемость жидкого азота.
338. Одной из пластин плоского конденсатора площадью S =0,2 м2 сообщили заряд q =10-9 Кл (другая пластина соединена с «землей»). Расстояние между пластинами d =2 мм. Между пластинами (параллельно им) находятся стеклянная (e =6) и эбонитовая (e =2,6) пластинки, толщины которых равны соответственно d1 =0,5 мм и d2 =1,5мм. Определить напряженность электрического поля в стекле и эбоните, а также поверхностные плотности связанных зарядов на них.
339. В однородное электрическое поле с напряженностью E0 =100 В/м помещена пластина из однородного и изотропного диэлектрика с проницаемостью e =2. Пластина расположена перпендикулярно к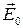 
. Определить электрическое смещение D и поляризованность диэлектрика P.
340. Плоский конденсатор заряжен до некоторой разности потенциалов. В конденсатор вдвинули диэлектрическую пластинку. После этого для восстановления прежней разности потенциалов пришлось увеличить заряд конденсатора в три раза. Найти диэлектрическую проницаемость пластинки.
341. Одинаковые заряды Q =100 нКл расположены в вершинах квадрата со стороной 10 см. Определить потенциальную энергию этой системы.
342. Площадь пластин плоского конденсатора 100 см2 и расстояние между ними 5 мм. Какая разность потенциалов была приложена к пластинам конденсатора, если известно, что при разряде конденсатора выделилось 4,19×10-3 Дж тепла?
343. Найти потенциальную энергию системы трех точечных зарядов:
q1 =10 нКл, q2 =20 нКл, q3 =-30 нКл, расположенных в вершинах равностороннего треугольника со стороной 10 см.
344. Два конденсатора, ёмкости которых С1 =600 пФ и С2 =1000 пФ, соединили последовательно. Батарею заряжают до разности потенциалов U =20 кВ. Затем конденсаторы, не разряжая, соединяют параллельно. Определить энергию разряда, происходящего при этом переключении.
345. 64 капли ртути, каждая радиусом r =1 мм и с зарядом q =1 нКл, находятся на бесконечном расстоянии друг от друга, а затем сливаются в одну каплю. Определить изменение энергии системы при этом процессе.
346. Точечный заряд q =3,0×10-8 Кл помещается в центре шарового слоя из однородного изотропного диэлектрика с e =3. Внутренний радиус слоя 250 мм,внешний - 500 мм. Найти энергию W, заключенную в диэлектрике.
347. Заряженный шар А радиусом 2 см приводится в соприкосновение с незаряженным шаром В, радиус которого 3 см. После того как шары разъединили, энергия шара В оказалась равной 0,4 Дж. Какой заряд был на шаре А до их соприкосновения?
348. Пластины плоского конденсатора площадью 100 см2 каждая притягиваются друг к другу с силой в 3×10-2 Н. Пространство между пластинами заполнено слюдой (e =6). Найти энергию в единице объема поля.
349. Плоский воздушный конденсатор с площадью пластин 100 см2 и расстоянием между ними в 1 мм заряжен до 100 В. Затем пластины раздвигаются до расстояния 25 мм. Найти энергию конденсатора до и после раздвижения пластин, если источник напряжения перед раздвижением отключается.
350. Плоский конденсатор заполнен диэлектриком и на его пластины подана некоторая разность потенциалов. Его энергия при этом равна 2×10-5 Дж. После того как конденсатор отключили от источника напряжения, диэлектрик вынули из конденсатора. Работа, которую надо было совершить против сил электрического поля, чтобы вынуть диэлектрик, равна 7×10-5 Дж. Найти диэлектрическую проницаемость диэлектрика.
351. К источнику ЭДС, равной 3 В, имеющему внутреннее сопротивление
1 Ом, подключена внешняя цепь, состоящая из двух параллельно соединенных сопротивлений по 4 Ом каждое. Найти разность потенциалов между клеммами источника напряжения.
352. Источник с ЭДС e = 2,0 В имеет внутреннее сопротивление r =0,5 Ом. Определить падение напряжения внутри источника при токе в цепи I =0,25 А. Найти внешнее сопротивление цепи при этих условиях.
353.Батарея гальванических элементов замкнута на внешнее сопротивление R1 =10 Ом и дает ток I1 =3 А. Если вместо сопротивления R1 включить сопротивление R2 =20 Ом, то ток I2 станет равным 1,6 А. Найти ЭДС и внутреннее сопротивление батареи.
354. Какова электродвижущая сила элемента, если при измерении напряжения на его зажимах вольтметром, внутреннее сопротивление которого 20 Ом, получают напряжение UV =1,37 В, а при замыкании элемента на сопротивление R =10 Ом в цепи возникает ток I =0,132 А?
355.В цепь, состоящую из батареи и резистора сопротивлением R =8 Ом, включают вольтметр, сопротивление которого RV =800 Ом, один раз последовательно резистору, второй – параллельно. Определить внутреннее сопротивление батареи, если показания вольтметра в обоих случаях одинаковы.
356. Источник ЭДС замыкается двумя последовательно соединенными сопротивлениями R1 и R2. Если вольтметр подключить к сопротивлению R1, то он покажет 6 В, если к R2 - 4 В, если вольтметр подключить к источнику, то он покажет 12 В. Найти действительные значения напряжений на сопротивлениях R1 и R2. Внутренним сопротивлением источника пренебречь.
357. Определить удельное сопротивление проводника длиной l =2 м, если при плотности тока j =106 А/м2 на его концах поддерживается разность потенциалов U =2 В.
358. Из медной проволоки длиной l =120 м и площадью поперечного сечения S =24 мм2 намотана катушка. Найти приращение сопротивления катушки при нагревании ее от t1 =20 оC до t2 =70 оC. Удельное сопротивление меди
r =17 нОм·м; температурный коэффициент сопротивления a =0,0043 C-1.
359. Лампа накаливания потребляет ток, равный 0,6 А. Температура вольфрамовой нити диаметром 0,1 мм равна 2200 оC. Ток подводится медным проводом сечением S =6 мм2. Определить напряженность электрического поля: 1) в вольфраме (удельное сопротивление при 0 оC r =55 нОм·м; температурный коэффициент сопротивления a =0,0045 oC-1); 2) в меди (температура подводящих проводов 20 оC).
360. Определить температурный коэффициент провода, составленного из алюминиевой проволоки сопротивлением 3 Ом (температурный коэффициент сопротивления a1 =0,0045 oC-1) и железной проволоки сопротивлением 2 Ом (температурный коэффициент сопротивления a2 =0,006 oC-1), соединенных последовательно.
361. Какая мощность выделяется в единице объема медного проводника длиной l =0,2 м, если на его концах поддерживается разность потенциалов U =4 В?
362. Проводник, состоящий из двух последовательно соединенных кусков медной проволоки одинаковой длины (l 1= l 2=10 м), но разного диаметра (d1=2d2), подключили к источнику ЭДС. По проводнику протекает ток 1 А, при этом в первом куске в виде тепла за две секунды выделилось 10 Дж. Найти удельную тепловую мощность тока в обоих кусках проволоки. Удельное сопротивление меди r =17 нОм·м.
363. Определить внутреннее сопротивление источника тока, если во внешней цепи при силе тока I1 =4 А развивается мощность P1 =10 Вт, а при силе тока
I2 =6 А - мощность P2 =12 Вт.
364. От источника, на клеммах которого разность потенциалов U =50 кВ, требуется передать мощность N =5·103 кВт на расстояние l =5 км. Допустимая «потеря» напряжения в проводах n =1 %. Найти минимальный диаметр медного провода, пригодного для данной цели.
365. Какое время требуется для нагревания 2 л воды (с =4,19×103 Дж/кг×К) от 20 оС до кипения в электрическом чайнике, если напряжение в сети 220 В, сопротивление спирали чайника 20 Ом, а КПД чайника 70 %?
366. Спираль электрического кипятильника имеет две секции. Если включена одна секция, вода закипает через t1 =10 мин, если другая, то через t2 =20 мин. Через сколько минут закипит вода, если обе секции включить: а) последовательно; б) параллельно? Напряжение на зажимах кипятильника и КПД установки считать во всех случаях одинаковыми.
367. При включении в сеть электроплитки с номинальной мощностью P0 =800 Вт разность потенциалов на клеммах розетки уменьшилась, а фактическая мощность электроплитки P1 стала равной 661 Вт. Какова мощность двух таких плиток, включенных параллельно в розетку? Изменением сопротивления плиток при изменении их накала пренебречь.
368. При каком сопротивлении внешней цепи источник с ЭДС e =10 В и внутренним сопротивлением r =20 Ом будет отдавать максимальную мощность? Какова величина этой мощности?
369. Электродвижущая сила батареи e =12 В. Наибольшая сила тока, которую может дать батарея, Imax =5 А. Какая наибольшая мощность может выделиться на подключенном к батарее резисторе с переменным сопротивлением?
370. Какое наименьшее число N одинаковых источников питания с ЭДС e =1 В и внутренним сопротивлением r =1 Ом необходимо взять, чтобы на внешнем сопротивлении R =10 Ом выделилась максимальная мощность? Максимальная сила тока Imax =2 А.
371. Какой заряд пройдет по проводнику, если в течение 10 с сила тока уменьшилась от Iо =10 А до 5 А? Считать, что сила тока уменьшается равномерно.
372. Какой заряд пройдет по проводнику, если в течение t =10 с сопротивление проводника равномерно возрастало, ток уменьшался от I1 =10 А до I2 =5 А, а разность потенциалов на концах проводника поддерживалась постоянной?
373. Сила тока в проводнике сопротивлением R =120 Ом равномерно возрастает от Iо =0 до Imax =5 А за время t =15 с. Определить выделившееся за это время в проводнике количество тепла.
374. По проводнику сопротивлением R =3 Ом течет равномерно нарастающий ток. Количество тепла, выделившегося за время t =8 с, равно Q =200 Дж. Определить заряд, прошедший за это время по проводнику. В момент времени, принятый за начальный, ток в проводнике был равен нулю.
375. Ток в проводнике сопротивлением R =15Ом равномерно возрастает от Iо =0 до некоторого максимального значения в течение времени t =5 с. За это время в проводнике выделилась в виде тепла энергия Q =10 кДж. Найти среднее значение силы тока в проводнике за этот промежуток времени.
376. На рис. 1 сопротивление каждого проводника, включенного между двумя узлами, равно 1 Ом. Найти сопротивление цепи.
377. Найти сопротивление цепи, изображенной на рис. 2. Считать, что сопротивление каждого проводника, включенного между узлами, равно 1 Ом.
378. 
Сопротивление каждого проводника, составляющего ребро куба, равно 10 Ом (рис. 3). Найти тепло, которое будет выделяться в этом кубе за одну секунду, если между точками A и B этого куба поддерживается разность потенциалов U =10 В.
379. Сопротивление каждого проводника, составляющего ребро куба, равно 10 Ом. Найти тепло, которое будет выделяться в этом кубе за одну секунду, если между точками A и C (рис. 3) этого куба поддерживается разность потенциалов U =10 В.
380.Определить ток, который будет протекать по проводам, подсоединенным к вершинам Bи Cкуба (рис. 3), составленного из сопротивлений величиной в 1 Ом, если он подключен к источнику тока с разностью потенциалов на выводах U =10 В.
Варианты контрольного задания № 3
| № варианта | Номера задач контрольного задания | |||||||
МАГНЕТИЗМ
Магнитное поле – одна из двух сторон электромагнитного поля, характеризующаяся воздействием на движущуюся электрически заряженную частицу с силой, пропорциональной заряду этой частицы и ее скорости. Кроме того, магнитное поле действует на проводники с током и на частицы и тела, обладающие магнитными моментами.
Магнитное поле создается проводниками с током, движущимися электрически заряженными частицами и телами, частицами и телами, обладающими магнитными моментами, а также изменяющимся во времени электрическим полем.
