Известно [2, 3, 9, 11], что облучение высокоэнергетическими заряженными частицами всегда приводит к первичной ионизации. Считается, что направление движения заряженной частицы сохраняется практически неизменным до тех пор, пока преобладают ионизационные потери энергии. В целом, высокоэнергетические заряженные частицы при прохождении через полупроводниковый материал теряют свою энергию за счет процессов электронного и ядерного торможения [12].
Электронное торможение представляет собой торможение высокоэнергетических ионов за счет кулоновского взаимодействия с атомарными электронами мишени. При передаче высоких энергий электронам решетки образуются дельта-излучение, высокоэнергетические электроны, которые рассеиваются от ионного трека, а также фотоны и рентгеновские кванты. При передаче атомам кристаллической решетки меньших энергий происходит возбуждение электронов и их переход в более высокоэнергетическую зону, в которой электроны термолизируют энергию путем испускания фотонов и фононов (нагрев) различных энергий. Наиболее общим эффектом рассеяния электронов и фотонов является эффект Комптона — взаимодействие между фотоном (рентгеновским квантом) и электроном, сопровождающееся передачей энергии электрону и испусканием фотона с меньшей энергией. В центре ионного трека доминируют возбужденные атомарные электроны, тогда как высокоэнергетические дельта-лучи рассеивают энергию по мере удаления от ионного трека. Процесс передачи энергии между фотонами, электронами и фононами каскадно приводит к меньшим и меньшим энергиям. Энергия иона поглощается в пределах более чем десятков нанометров.
Ядерное торможение происходит за счет упругого рассеяния высокоэнергетических ионов на ядрах атомов мишени. Данные процессы приводят к смещениям атомов из узлов решетки, и о них подробно говорилось выше (см. п. 1.3.2).
Экспериментально определенное значение энергии ионизации, необходимой для образования электронно-дырочных пар, в Si составляет 3,6 эВ, в GaAs — 4,8 эВ, в SiO2 — 17 эВ [12]. Однако многие расчетно-экспериментальные результаты говорят о том, что имеет место корреляция с шириной запрещенной зоны полупроводника. В [12] приводятся аппроксимационные формулы для этой корреляции:
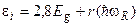, где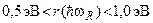 
; (1.21)
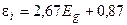. (1.22)
Первое слагаемое в обоих выражениях — это энергия ударной ионизации, а второе слагаемое — потери энергии на оптические фононы; r — среднее количество фононов, генерируемых в одном событии;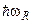 
— рамановский квант, энергия каждого оптического фонона. Выражение (1.21) описывает корреляцию между энергией ионизации и шириной запрещенной зоны для широкозонных полупроводников, а (1.22) — для узкозонных.
Следует отметить, что среднее значение энергии ионизации зависит от температуры и вида ионизирующего излучения, и эти значения могут существенно варьироваться [12].
Для каждого иона, проходящего через полупроводник, количество переданной кристаллу энергии на единицу длины определяется как линейные потери энергии (ЛПЭ). Определение ЛПЭ задается выражением (1.1). Значение ЛПЭ варьируется в зависимости от материала. Плотность кристаллической структуры и размер атомов непосредственно влияет на плотность полупроводника, а, следовательно, на эффективность процесса передачи энергии, т.е. на величину ЛПЭ. Как правило, материалы с меньшей плотностью характеризуются меньшими значениями ЛПЭ. Другим моментом, влияющим на величину ЛПЭ, является скорость падающего иона. Обычно тяжелые ионы взаимодействуют с кристаллической решеткой посредством кулоновских сил. Энергия, переданная падающим ионом при взаимодействии с другими заряженными частицами (атомами кристалла) характеризуется произведением кулоновской силы и времени взаимодействия двух частиц. Если ион попадает в кристалл, имея очень высокую скорость, то время, в течение которого он может передать свою энергию атомам решетки, очень мало [12]. По мере прохождения иона через полупроводник меняется его энергия и ЛПЭ. Типичная зависимость ЛПЭ от текущего значения глубины проникновения иона имеет немонотонный характер. Вначале наблюдается рост ЛПЭ и достижение максимального значения (пик Брега), затем наблюдается спад ЛПЭ. Максимальное значение ЛПЭ наблюдается в пике Брэгга. В этом случае ион наиболее эффективно передает свою энергию кристаллу. Обычно эта область эффективной передачи энергии лежит в конце пробега иона в кристалле. Поперечное сечение кулоновских взаимодействий вычисляется из Резерфордовского радиуса рассеяния rd [12]:
,
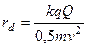где Q — заряд атома мишени; k — кулоновская константа; q, m и v — заряд, масса и скорость падающей частицы.
Основной характеристикой является кинетическая энергия падающей частицы, таким образом, более высокоэнергетические частицы имеют меньшее поперечное сечение рассеяния.
Следует отметить, что кулоновское взаимодействие не является единственным видом взаимодействий [12]. При существенно меньших значениях поперечного сечения могут иметь место ядерные взаимодействия. Ядерное взаимодействие (рассеяние) может быть двух видов:
· упругое — когда ядерные силы отталкивают атом решетки от падающего тяжелого иона;
· неупругое — когда поглощаются ядра двух атомов и возникает новая частица.
В обоих случаях перемещается атом решетки (смещение) и/или создается новый движущийся ион (ионы). Возникшие ионы приобретают энергию из события рассеяния и затем отдают ее в последующих взаимодействиях.
Расчет ЛПЭ для различных ионов в различных мишенях можно провести в среде SRIM (http://www.srim.org/). Результаты таких расчетов для некоторых ионов в кремнии приведены на рис. 1.12, а.
Высокоэнергетические электроны, как и ионы, испытывают потери энергии как в результате взаимодействий упругого рассеяния, так и путем ионизации. Торможение быстрых электронов в веществе сопровождается ионизационными потерями и сильным рассеянием вследствие малой массы электронов. Упругое рассеяние играет в общем балансе потерь энергии относительно слабую роль по сравнению с ионизационными потерями [4]. Ионизационные потери энергии электронов в кремнии в зависимости от их энергии приведены на рис. 1.12, б [7].
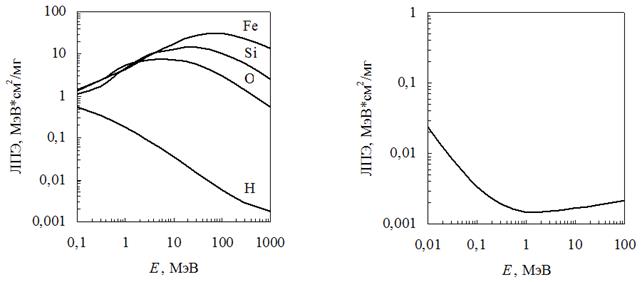
а б
Рис. 1.12. Энергетические зависимости ионизационных потерь энергии в кремнии для некоторых ионов (а) и электронов (б)
С повышением энергии электронов возрастает роль радиационных потерь энергии, связанных с испусканием электромагнитного излучения при торможении электронов в веществе (тормозное излучение). Радиационные потери энергии быстрых электронов существенно зависят от степени экранирования ядра атомарными электронами. Спектр тормозного излучения непрерывен от нуля до максимального значения, равного кинетической энергии электрона. Тормозное излучение обладает более высокой проникающей способностью, чем вызвавшее его электронное, и может вносить существенный вклад в формирование внутренней дестабилизирующей обстановки. Отношение радиационных потерь энергии электрона к ионизационным выражается формулой Бете-Гайтлера. Если энергию Е электрона измерять в мегаэлектронвольтах, то
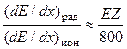, (1.23)
где Z — заряд ядра атома мишени.
Из выражения (1.23) следует, что кремнии и алюминии радиационные потери становятся сравнимыми с ионизационными при энергии электронов порядка 60 МэВ, кроме того, при неизменной энергии электронов роль радиационных потерь возрастает с увеличением атомного номера облучаемого вещества.
