Создать новый лист «Задание 5».
Найти один из корней нелинейного уравнения. Выполнение индивидуального задания должно состоять из следующих пунктов:
Отделение корня графическим методом - необходимо построить график функции, приведённой в задании, и найти хотя бы один отрезок, где он пересекает ось X, это будет приблизительное значение корня. Если ни одного отрезка найти не удалось, нужно изменить область построения.
Уточнение корня - используя два специальных средства: «Подбор параметра» и «Поиск решения», сузить найденный отрезок до 0,001. Это и будет значение корня с точностью до 0,001.
Простейшим случаем задачи оптимизации является определение корня нелинейного уравнения. Уравнение f (х) = 0 будет нелинейным, если в его правой части присутствует неизвестная в степени, отличной от 1, или имеются трансцендентные функции sin(x), Ln(x) и т.д. Для некоторых уравнений существуют методы, позволяющие получить точное решение (например, квадратное уравнение). Однако большинство из них не имеет точного аналитического решения.
Чаще всего нелинейное уравнение имеет несколько корней, поэтому его приближённое решение состоит из двух этапов.
На первом этапе производится грубый подбор или отделение корня, то есть находятся все или хотя бы один отрезок, на котором есть корень. Для этого следует просчитать таблицу значений функции на произвольно выбранном интервале и построить график. Напомним, что корень - это значение х, при котором левая часть уравнения равна 0. На графике это отрезок, на котором функция пересекает ось X, соответственно в таблице -отрезок на котором функция меняет знак. Если на выбранном интервале корней не оказалось, следует поискать их на другом отрезке, просто изменив значения в столбце аргументов.
На втором этапе отделённый корень определяется с заданной точностью. Для этого можно использовать средство «Подбор параметра» (ДАННЫЕ – АНАЛИЗ «ЧТО ЕСЛИ…» _ «ПОДБОР ПАРАМЕТРА». Для этого нужно заполнить на рабочем листе две ячейки: в одной записать значение аргумента, а во второй формулу для расчета функции, являющейся левой частью уравнения. Эти ячейки можно просто скопировать из таблицы. В качестве начального значения аргумента X следует выбрать левую границу отрезка, на котором обнаружен корень. С таким же успехом можно для этой цели можно использовать средство «Поиск решения» (ДАННЫЕ – ПОИСК РЕШЕНИЯ). Поскольку «Поиск решения» позволяет задавать ограничения, можно легко найти все отделенные корни, задавая в качестве ограничений границы отрезков, на которых обнаружены корни.
Задание:
Найти один из корней нелинейного уравнения:
Решение
Порядок действий:
Ø Отделить корни графическим методом, для этого построить график функции 
и найти хотя бы одно пересечение графика с осью X. Отрезок, на котором график функции пересекает ось X, является базовым для дальнейшего уточнения корня.
Ø Для уточнения значения корня использованы средства «Подбор параметра» и «Поиск решения». В обоих случаях в качестве начального значения X выбираем левую границу отрезка, на котором есть корень.
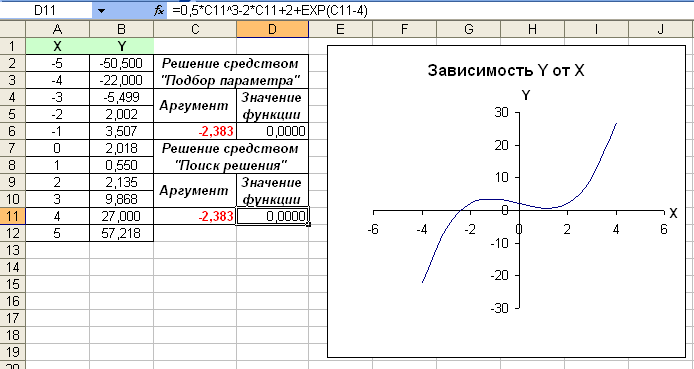
Как видно из таблицы и графика функции имеет корень, на отрезке [-3;-2]. Для уточнения корня используем средства «Подбор параметра» и «Поиск решения». В обоих случаях значения корня X=-2,383.
Настройка окон «Подбор параметра» и «Поиск решения».
На рисунке показан пример заполнения окна «Поиск решения» и дополнительной формы «Добавление ограничения» при решении задачи нахождения корней нелинейного уравнения.
