Трьохопорну лопатку розраховують на міцність (рис. 5.6, а і б) як балку змінної жорсткості, навантажену рівномірно розподіленим гідравлічним навантаженням, інтенсивність якого на одиницю довжини пера рівна
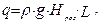(5.1)
де L - ширина площини пера, що піддається тиску; Нроз=Нст.макс·(1+ξ) - напір при скиданні навантаження при положенні лопаті, що відповідає найменшому моменту інерції у площині згину (рис. 5.6, а). При цьому складова сили важеля, діє у розрахунковій площині, рівна
(5.2)
де сила важеля 
- сила, що прикладена нормально до осі важеля на плечі, що визначається із рівняння привідного момента. Вирішення задачі з усуненням статичної невизначності шляхом заміни реакції на третій опорі С силою і визначенням оптимального зазора на цій опорі розроблене А. Е. Жмудем.
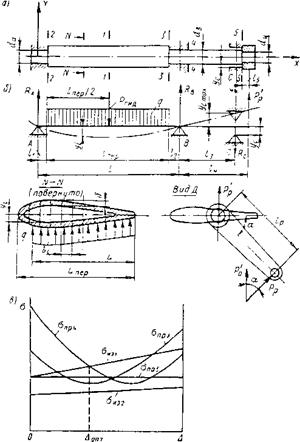
Рис. 5.6. До розрахунку трьохопорної лопаті напрямного апарату на міцність:
а – конструктивна схема; б – схема навантаження лопаті;
в – графік для вибору оптимального зазора у верхній опорі
Розрахунок виконують у такій послідовності:
1) будують схему вантаження лопаті (рис. 5.6, б) і визначають усі розмірні характеристики; при цьому мають бути виконані креслення і побудова напрямного апарату;
2) будують профіль пера і графоаналітичним методом визначають координату нейтральної осі у'с і найменший момент інерції перерізу J1; із побудови визначають у'ст.макс;
3) знаходять за (5.3) значення відносних величин і за (5.4) - сумарні значення розмірних і геометричних характеристик;
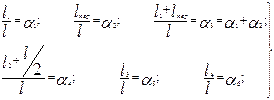(5.3)
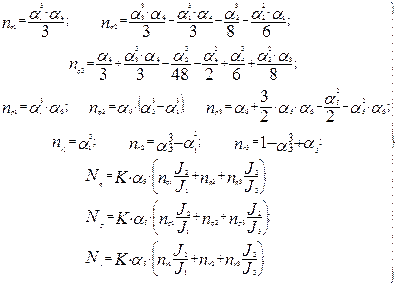(5.4)
4) визначають за (5.5) гідравлічну силу Ргідр і за (5.6) гідравлічний момент Мгідр в закритому стані, і рівномірно розподілене гідравлічне навантаження q із (5.7);
(5.5)
(5.6)
де Нмакс – найбільший статичний напір відносно середньої лінії напрямного апарата; Fпер=b0·L – площа пера, що піддається гідравлічному тиску; b0 - висота напрямного апарату; L - ширина профіля, що піддається тиску; 
- ексцентриситет, що рівний плечу момента або відстані між точкою прикладення сили Ргідр і віссю повороту лопаті;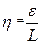 
- відносний ексцентриситет (ексцентриситет вважається додатнім при позитивному моменті);
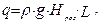(5.7)
де L - ширина площини пера, що піддається тиску; Нроз=Нст.макс·(1+ξ) - напір при скиданні навантаження при положенні лопаті, що відповідає найменшому моменту інерції у площині згину (рис. 5.6, а).
5) одночасно з визначенням зусилля серводвигунів, методом послідовних наближень, задаючись реакціями або моментом тертя (наприклад, починаючи з Мтр =0), знаходять із (5.8) Рр, а із (5.9) Рр1, що відповідають цим моментам, вважаючи при цьому уС =0; визначають за (5.10) силу серводвигунів;
(5.8)
(5.9)
(5.10)
де 
- коефіцієнт передачі ланок механізму; 
- кінематичний коефіцієнт, що залежить від розташування ланок.
6) задаючись рядом уС за (5.11) і (5.12), отримують значення прогинання від сили гідравлічного тиску на лопать уСq та значення прогинання від сили важеля уСр і відповідні їм значення RС;
(5.11)
(5.12)
де J – моменти інерції перерізів.
7) остаточно уточнюють за (5.13) і (5.14) відповідні значення реакцій RА та RВ, силу серводвигунів і зусилля важеля;
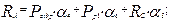(5.13)
(5.14)
8) після уточнення реакцій для усіх прийнятих значень уС визначаємо згинальну напругу за (5.15)÷(5.19) і напругу кручення за (5.20), (5.21), а за (5.22) - приведену напругу. За (5.23) перевіряємо питомі тиски у опорах.
Згинальне напруження у пері лопаті в перерізі 1-1 визначається при 
, що приймаються за найбільші
(5.15)
де W1 – момент опору; для розтягнутих волокон 
, для стиснених волокон 
Згинальні напруження у перерізах 2-2, 3-3, 4-4, 5-5 рівні
(5.16)
(5.17)
(5.18)
(5.19)
де Wі≈0,1·d3і – відповідні моменти опору цапф.
У перерізах 3-3, 4-4 і 5-5 крім згинального діє крутний момент, що створюється важелем. Напруги кручення відповідно рівні
(5.20)
(5.21)
Приведені напруги визначаються за третьою теорією міцності. У перерізах 3-3, 4-4 і 5-5 вони відповідно рівні
(5.22)
Втулки лопатей перевіряють на питомий тиск за формулою
(5.23)
де Rі – реакція опори; Fі - площа проекції опори на діаметральний переріз; lі - довжина частини цапфи, що опирається на втулку; dі - діаметр цапфи.
9) Відповідно до рис. 5.6, в, будують графік і вибирають оптимальний зазор уС.опт, для якого і фіксуються розрахункові значення напруги.
Розрахунок зручно вести у табличній формі. Розрахунок ведуть при закритому положенні апарату. При декількох відкриттях в уточнених розрахунках визначаються тільки реакції опор.
Існують методи розрахунку, у яких моменти визначають графоаналітичним способом, а для визначення прогинів використовують правило Верещагіна і інтеграл Максвелла-Мора, які призводять також до дуже складних виразів і підрахунків, але оптимальний зазор при цьому визначається однозначно.
