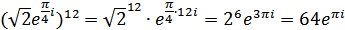Рассмотрим применение формул Крамера к решению систем двух линейных уравнений с двумя неизвестными.

Решение. Вычислим определитель системы и определители х и у:

Найдем значение х и у по формуле Крамера:

Итак, решение системы есть (3:-1).
72. Решите систему уравнений

Решение. Вычислим определитель системы и определители х и у:

Так как =0, а х≠0, у≠0, то система не имеет решений (уравнения противоречивы).
73. решить систему уравнений
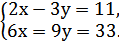
Решение. Находим

Данная система имеет бесчисленное множество решений (коэффициенты при неизвестных пропорциональны).
74. Решить систему уравнений

Решение. Вычислим определить системы и определители при неизвестных:



Найдем значения x, y, z по формулам Крамера.

Итак, получаем ответ: (1;-1;2).
Тема 3. Решение систем линейных уравнений методом Гаусса.
При решении систем линейных уравнений используют также метод Гаусса (метод последовательного исключения неизвестных). Он состоит в следующем: систему уравнений приводят к эквивалентной ей системе с треугольной матрицей (системы называются эквивалентными, если множества их решений совпадают). Эти действия называют прямым ходом. Из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).
При выполнении прямого хода используют следующие преобразования:
1. Умножение или деление коэффициентов свободных членов на одно и то же число;
2. Сложение и вычисление уравнений;
3. Перестановку уравнений системы;
4. Исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободных членов равны нулю.
Используя метод Гаусса, решить систему уравнений.
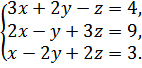
Решение. Переставим третье уравнение на место первого:

Запишем расширенную матрицу:
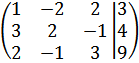
Что бы в 1-м столбце получить а21=а31=0, умножим 1-ю строку на 3, а затем на 2 вычтем результаты из 2-й и 3-й строк:

Разделим 20-ю строку на 8, полученные результаты умножим на 3 и вычтем из 3-й строки:

Запишем новую эквивалентную систему, которой соответствует расширенная матрица:

Выполняя обратный ход, с помощью последовательных подставок находим неизвестные:
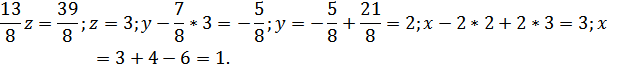
Итак, получаем ответ: (1; 2: 3).
Тема 4. Дифференцирование
а) Найти экстремумы функции
б) наибольшее и наименьшее значение функции [-1;3]

Решение.
1. Найти y|: y|=x3+3x2+2x;
y|=0;
x3+x2+2x=0;
x(x2+3x+2)=0; т.е. x1=-1; x2=0; x3=-2 – критические точки.
2. Найти y|| : y||=3x2+6x+2
Найти значение y|| при критических точках
ymin (-2)=4; т.к. y||=(-2)>0 т.е. функция имеет min;
ymax(-1)=17/4;т.к. y||=(-1)<0 т.е. функция имеет max;
ymin (0)=4; т.к. y||=(0)>0 т.е. функция имеет min;
б) Для нахождения наибольшего или наименьшего значения находят критические точки, принадлежащие отрезку [-1;3], значения f(x) при этих критических точках и на концах отрезка; среди найденных значений выбирают f наибольшее и f наименьшее.
1. y|= x3+3x2+2x=0;
| Î[-1;3] |
x2=-1
Найдем 


f наибольшее (3)=60,25
f наименьшее (0)= 4
Примеры решения по теме 5: Интегральные исчисления
а) Вычислить 
Данный интеграл вычисляется методом замены переменной.
Решение:
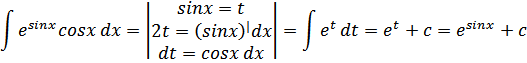
Проведем дифференцирование:
 – подынтегральная функция
– подынтегральная функция
б) Вычислить 
Решение: интеграл вычисляется по частям: 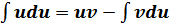
r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
Аналогично можно проверить. Что произведение полученной функции равно подынтегральной функции, т.е интеграл вычислен правильно.
в) Вычислить 
Решение.
При вычислении переделенного интеграла используются такие же методы что и неопределенного. Но затем пользуются формулой Ньютона- Лейбница:


г) Найти площадь фигуры: у=х2-2х – парабола с вершиной в точке (1;-1), ветви вверх точка пересечения с осью ОХ: (0;0); (2;0)

s=s1+s2;
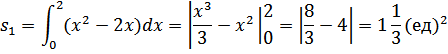


Тема: Комплексные числа. Алгебраическая форма комплексного числа a+bi; {a,b}ªR, i- мнимая единица, i2=-1
Сложение:
z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i
(2+3i)+(5-7i)=(2+5)+(3-7)i=7-4i
Вычитание:
z1-z2 =(a+bi)-(c+di)=(a-c)+(b-d)i
(5+4i)-(2-3i)=(5-2)+(4+3)i=3+7i
Умножение:
z1*z2=(a+bi)*(c+di)=(ac-bd)+(ad+bc)i
(a+bi) на (c+di) умножаем по правилам действий над многочленами.
(1+2i)(3-i)=3*1-1*i+6i-2i2=3+2-i+6i=5+5i
Деление: на практике при делении комплексных чисел удобно домножить числитель и знаменатель дроби на выражении, сопряженное знаменателю:

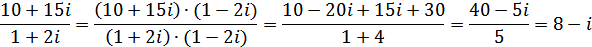
Возведение в степень мнимой единицы:
i1=i;
i2=-1;
i3=i2*i=-1*i=-i;
i4=i2 *i2=(-1)(-1)=1;
i5=i3*i2=-i(-1)=i;
i6=i5*i=i*i=-1=i2;…
Видим закономерность:
i(4n+r)=(i4)n*ir=(1)n*ir=ir
Получаем:
i4m=1;
i4m+1=i;
i4m+2=-1;
i4m+3=-i;
i218=i4*54+2=i2=-1.
Сумма и произведение двух сопряженных комплексных чисел являются действительными числами:
z+z=(a+bi)+(a-bi)=2a;
z*z=(a+bi)(a-bi)=a2+b2.
Каждому комплексному числу z=a+bi можно поставить в соответствие точку M(a;b) координатной плоской, абсцисса которой равна действительной части комплексной части комплексного числа, а ордината - мнимой части. (рис.)

Рис.
Важной и удобной является интерпретация комплексного числа a+bi как радиус - вектора OM, т.е. вектора, исходящего из начала координат O(0,0) и идущего в точку M(a;b). Разумеется, вместо радиус вектора OM можно взять любой равный ему вектор. Изображение комплексных чисел с помощью векторов удобно тем, что при этом получают простое геометрическое истолкование операций над ними. При сложении чисел z1=a+bi и z2=c+di складываются их действительные и мнимые части. При сложении соответствующих им векторов OM1 и OM2 складываются их координаты:
числу z1+z2 соответствует вектор OM1+OM2,
числу z1-z2 – вектор OM1 – OM2.
Модулем комплексного числа z1=a+bi называется арифметический квадратный корень из суммы квадратов его действительной части и коэффициента при мнимой единице:

Аргументом комплексного числа z1=a+bi называется радианная мера угла φ, образованного этим вектором с положительным направлением действительной оси 0≤φ<2π,
arg z=φ
Величина угла считается положительной, если отсчет ведется против часовой стрелки и отрицательной, если отсчет производится по часовой стрелке.
Возьмем на плоскости точку М(a,b), пусть ей соответствует комплексное число z1=a+bi. Обозначим через φ угол, который образует радиус – вектор OM с положительным направлением оси OX.
Тригонометрическая форма комплексного числа r(cosφ+ isinφ), показательная форма reφi
Действия в показательной форме:
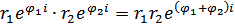
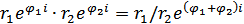
 - формула Муавра.
- формула Муавра.
Аналогично в тригонометрической форме:
Пример.