- Дайте определения дифференциального уравнения первого порядка и его общего и частного решения (интеграла). Сформулируйте задачу Коши для дифференциального уравнения первого порядка и укажите ее геометрический смысл.
- Дайте геометрическое истолкование дифференциального уравнения первого порядка, выясните геометрический смысл общего и частного решений.
- Сформулируйте теорему о существовании и единственности решения дифференциального уравнения первого порядка.
- Дайте определение дифференциального уравнения с разделяющимися переменными. Изложите метод нахождения его общего решения. Приведите пример.
- Дайте определение однородного дифференциального уравнения первого порядка. Изложите метод нахождения его общего решения. Приведите пример.
- Дайте определение линейного дифференциального уравнения первого порядка. Изложите метод нахождения его общего решения. Приведите пример.
- Дате определение уравнения Бернулли. Изложите метод нахождения его общего решения. Приведите пример.
- Что называется особым решением дифференциального уравнения первого порядка?
- Сформулируйте теорему о существовании и единственности решения дифференциального уравнения второго порядка.
- Изложите метод решения дифференциального уравнения вида
. Приведите пример. - Изложите метод решения дифференциального уравнения вида
. Приведите пример. - Изложите метод решения дифференциального уравнения вида
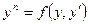. Приведите пример. - Дайте определение линейного дифференциального уравнения n -го порядка (однородного и неоднородного). Докажите основные свойства частных решений линейного однородного дифференциального уравнения.
- Дайте определение линейно зависимых и линейно независимых функций и приведите примеры. Докажите, что для линейно зависимых функций определитель Вронского равен нулю.
- Докажите теорему об общем решении линейного однородного дифференциального уравнения второго порядка.
- Выведите формулу для общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае действительных различных корней характеристического уравнения. Приведите пример.
- Выведите формулу для общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае комплексных корней характеристического уравнения. Приведите пример.
- Выведите формулу для общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае равных корней характеристического уравнения. Приведите пример.
- Докажите теорему об общем решении линейного неоднородного дифференциального уравнения второго порядка.
- Изложите правило нахождения частного решения линейного дифференциального уравнения второго порядка с постоянными коэффициентами и правой частью вида
, где 
- многочлен степени 
. - Изложите правило нахождения частного решения линейного дифференциального уравнения второго порядка с постоянными коэффициентами и правой частью вида
.
- Что называется нормальной системой дифференциальных уравнений первого порядка? Сформулируйте задачу Коши для этой системы.
- Изложите метод нахождения общего решения нормальной системы дифференциальных уравнений первого порядка сведением системы к одному дифференциальному уравнению (метод исключения). Приведите пример.
- Изложите метод нахождения общего решения нормальной системы двух линейных дифференциальных уравнений с постоянными коэффициентами в случае простых корней характеристического уравнения. Приведите пример.
Ряды
- Дайте определение сходящегося и расходящегося рядов. Исследуйте сходимость ряда, составленного из членов геометрической прогрессии.
- Докажите необходимый признак сходимости ряда.
- Докажите, что отбрасывание конечного числа членов ряда не изменяет его сходимости (расходимости). Покажите, что сумма ряда равна сумме первых n членов, сложенной с суммой ряда, полученного из данного отбрасыванием этих n членов.
- Докажите теорему о сравнении рядов с положительными членами. Приведите пример применения этого признака.
- Докажите признак Даламбера сходимости знакопеременных рядов. Приведите пример применения этого признака.
- Докажите признак Коши сходимости рядов с положительными членами. Приведите пример применения этого признака.
- Докажите интегральный признак сходимости ряда Коши. Приведите пример применения этого признака.
- Дайте определение абсолютно сходящегося ряда. Докажите, что из абсолютной сходимости ряда следует его сходимость. Сформулируйте свойства абсолютно сходящихся рядов. Приведите примеры абсолютно и условно сходящихся рядов.
- Докажите признак Лейбница сходимости знакочередующихся рядов. Приведите пример на применение этого признака. Покажите, что при замене суммы ряда Лейбница суммой первых его членов допускаемая абсолютная погрешность не превосходит модуля первого отброшенного члена.
- Дайте определение понятия равномерной сходимости последовательности функций. Какой ряд называется равномерно сходящимся?
- Сформулируйте признак Вейерштрасса абсолютной и равномерной сходимости ряда.
- Сформулируйте основные свойства равномерно сходящихся рядов.
- Докажите теорему Абеля о сходимости степенных рядов.
- Выведите формулу для вычисления радиуса круга сходимости степенного ряда.
- Выведите условия разложимости функции в ряд Тейлора.
- Разложите функцию
в степенной ряд и докажите с помощью остаточного члена сходимость полученного ряда к данной функции - Разложите функцию
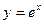в степенной ряд и докажите с помощью остаточного члена сходимость полученного ряда к данной функции. - Разложите функцию
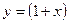в степенной ряд и найдите промежуток сходимости полученного ряда. - Сформулируйте теорему об интегрировании степенных рядов и с ее помощью получите разложение в ряд функции
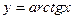. - Сформулируйте теорему об интегрировании степенных рядов и с ее помощью получите разложение в ряд функции
. - Сформулируйте теорему о дифференцировании степенных рядов и с ее помощью получите разложение в ряд функции
. - Приведите пример оценки точности вычисления суммы знакочередующегося ряда.
- Приведите пример применения остаточного члена формулы Тейлора (в форме Лагранжа) к оценке точности вычисления с помощью степенного ряда.
- Изложите метод приближенного вычисления определенных интегралов с помощью рядов. Приведите примеры.
- Изложите метод приближенного интегрирования дифференциальных уравнений с помощью степенных рядов. Приведите пример.
- выведите формулы для коэффициентов ряда Фурье.
- Сформулируйте достаточные условия разложимости функции в ряд Фурье. Приведите примеры функций, удовлетворяющих и не удовлетворяющих этим условиям.
- Выведите формулы для коэффициентов ряда Фурье для четных и нечетных функций.
- Представьте ряд Фурье в комплексной форме.
- Что называется интегралом Фурье?
- Дайте определение преобразования Фурье и сформулируйте его основные свойства.
Список литературы
1. Шипачев, В. С. Высшая математика: учебник для вузов / В. С. Шипачев. - 8-е изд., стер. - М.: Высшая школа, 2006. - 479с.
2. Данко, П. Е. Высшая математика в упражнениях и задачах / П. Е. Данко, А.. Г. Попов, Т. Я. Кожевников. В 2-х ч. Ч. 1. – 4-е изд., испр. и доп. – М.: Высшая школа, 1986. – 304 с.; Ч. II. – 4-е изд., испр. и доп. – М.: Высшая школа, 1986. – 415 с.
3. Меркулов, В. А. Курс высшей математики. Избранные разделы: учеб. пособие / В. А. Меркулов. – Волгоград: ВолгГАСУ, 2004.
4. Минорский, В. П. Сборник задач по высшей математике / В. П. Минорский. – М.: Наука, 1977. – 352 с.
5. Письменный, Д. Т. Конспект лекций по высшей математике. 2 часть. / Д. Т. Письменный. – М.: Рольф, 2001. – 288 с.
6. Рябушко, А. П. Сборник индивидуальных заданий по высшей математике. Часть 2 / А. П. Рябушко [и др.]. – Мн.: Выш. шк., 1992.
