1. Равенство вида  , содержащее независимую переменную x, искомую функцию y = y (x) и ее производные какого-либо порядка, называется дифференциальным уравнением.
, содержащее независимую переменную x, искомую функцию y = y (x) и ее производные какого-либо порядка, называется дифференциальным уравнением.
2. Натуральное число n, являющееся порядком старшей производной, называется порядком дифференциального уравнения.
3. Дифференциальным уравнением 1-го порядка называется уравнение вида  или в дифференциалах
или в дифференциалах  . Если эти равенства можно разрешить относительно производной, то их записывают в виде
. Если эти равенства можно разрешить относительно производной, то их записывают в виде  или
или  .
.
4. Решением дифференциального уравнения 1-го порядка называется функция y = j(x), имеющая непрерывную производную  на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство.
на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство.
5. Задача Коши для дифференциального уравнения 1-го порядка: требуется найти решение y = j(x) уравнения, удовлетворяющее начальному условию y = y 0 при x = x 0.
6. Общим решением дифференциального уравнения 1-го порядка называется функция y = j(x; С), содержащая произвольную постоянную С и удовлетворяющая условиям: 1) при любых начальных условиях (x 0; y 0) уравнение y 0 = j(x 0; С) должно быть разрешимо относительно С так, что С = y(x 0; y 0); 2) при всех значениях постоянной С = y(x 0; y 0) функция y = j(x; y(x 0; y 0)) должна удовлетворять дифференциальному уравнению.
7. Всякое решение, получаемое из общего при фиксированном значении постоянной С называется частным решением дифференциального уравнения.
8. Уравнение вида  или
или  называется дифференциальным уравнением с разделяющимися переменными. Приводятся к виду
называется дифференциальным уравнением с разделяющимися переменными. Приводятся к виду 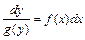 или
или  путем разделения переменных x и y и затем почленно интегрируются.
путем разделения переменных x и y и затем почленно интегрируются.
9. Уравнение вида  называется однородным дифференциальным уравнением. Используется замена:
называется однородным дифференциальным уравнением. Используется замена:  или
или  , где
, где  – новая неизвестная функция, тогда
– новая неизвестная функция, тогда  . Сводится к дифференциальному уравнению с разделяющимися переменными относительно новой функции, для которого находят общее решение. Записывают общее решение исходного уравнения по формуле
. Сводится к дифференциальному уравнению с разделяющимися переменными относительно новой функции, для которого находят общее решение. Записывают общее решение исходного уравнения по формуле  .
.
10. Уравнение вида 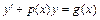 называется линейным дифференциальным уравнением. Используется метод Бернулли:
называется линейным дифференциальным уравнением. Используется метод Бернулли: 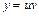 , где
, где  ,
,  – новые неизвестные функции, тогда
– новые неизвестные функции, тогда 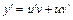 . Получаем:
. Получаем:  или
или  . Подберем функцию v так, чтобы выражение в скобках было равно нулю, тогда получаем
. Подберем функцию v так, чтобы выражение в скобках было равно нулю, тогда получаем  Первое уравнение – ДУ с разделяющимися переменными, находим его частное решение при С = 0. Найденное частное решение подставляем во второе уравнение, являющееся тоже ДУ с разделяющимися переменными и находим его общее решение. Записываем общее решение исходного уравнения по формуле
Первое уравнение – ДУ с разделяющимися переменными, находим его частное решение при С = 0. Найденное частное решение подставляем во второе уравнение, являющееся тоже ДУ с разделяющимися переменными и находим его общее решение. Записываем общее решение исходного уравнения по формуле 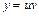 .
.
11. Уравнение вида  , где
, где  называется дифференциальным уравнением Бернулли. Используется метод Бернулли:
называется дифференциальным уравнением Бернулли. Используется метод Бернулли: 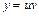 .
.
12. Дифференциальным уравнением 2-го порядка называется уравнение вида 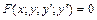 . Если уравнение можно разрешить относительно
. Если уравнение можно разрешить относительно  , то его записывают в виде
, то его записывают в виде  .
.
13. Решением дифференциального уравнения 2-го порядка называется функция y = j(x), имеющая непрерывные производные  ,
,  на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство.
на некотором интервале (a; b) и обращающая уравнение в верное числовое равенство.
14. Задача Коши для дифференциального уравнения 2-го порядка: требуется найти решение y = j(x) уравнения, удовлетворяющее начальным условиям y = y 0, 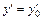 при x = x 0.
при x = x 0.
15. Общим решением дифференциального уравнения 2-го порядка называется функция y = j(x; С 1; С 2), содержащая две произвольные постоянные С 1, С 2 и удовлетворяющая условиям: 1) при любых начальных условиях  система уравнений
система уравнений  должна быть разрешима относительно постоянных С 1, С 2 так, что
должна быть разрешима относительно постоянных С 1, С 2 так, что  2) при всех значениях этих постоянных С 1, С 2 функция y = j(x; C 1; C 2) обращает дифференциальное уравнение в верное числовое равенство.
2) при всех значениях этих постоянных С 1, С 2 функция y = j(x; C 1; C 2) обращает дифференциальное уравнение в верное числовое равенство.
16. Всякое решение, получаемое из общего при фиксированных значениях постоянных С 1, С 2 называется частным решением дифференциального уравнения.
17. Дифференциальные уравнения 2-го порядка, допускающие понижение порядка:
а)  решается повторным интегрированием.
решается повторным интегрированием.
б)  , явно не содержащее искомой функции
, явно не содержащее искомой функции  . Используется замена:
. Используется замена: 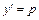 , где
, где 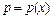 – новая неизвестная функция, тогда
– новая неизвестная функция, тогда  . Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу
. Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу 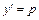 . Получаем ДУ с разделяющимися переменными относительно функции y, находим его общее решение.
. Получаем ДУ с разделяющимися переменными относительно функции y, находим его общее решение.
в) 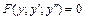 , явно не содержащее независимой переменной
, явно не содержащее независимой переменной  . Замена:
. Замена: 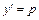 , где
, где 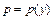 , тогда
, тогда  . Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу
. Для нового уравнения относительно функции p находим общее решение и подставляем его в формулу 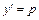 . Получаем ДУ с разделяющимися переменными относительно функции y, находим его общее решение.
. Получаем ДУ с разделяющимися переменными относительно функции y, находим его общее решение.
18. Линейным однородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами называется уравнение вида  . Составляется характеристическое уравнение
. Составляется характеристическое уравнение  .
.
Если  , то
, то  и общее решение исходного уравнения имеет вид:
и общее решение исходного уравнения имеет вид: 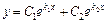 .
.
Если  , то
, то  и
и 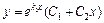 .
.
Если  , то
, то  и
и 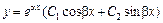 .
.
19. Линейным неоднородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами с правой частью специального вида называется уравнение вида  . Его общее решение ищется в виде
. Его общее решение ищется в виде 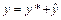 , где
, где  – общее решение соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами:
– общее решение соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами:  , а
, а  – какое-либо частное решение исходного уравнения.
– какое-либо частное решение исходного уравнения.
Если  , где a – некоторое число, Pn (x) – многочлен степени n, то
, где a – некоторое число, Pn (x) – многочлен степени n, то  , где
, где 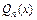 – многочлен степени
– многочлен степени  с неопределенными коэффициентами,
с неопределенными коэффициентами,  – число, равное кратности a как корня характеристического уравнения
– число, равное кратности a как корня характеристического уравнения  соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами
соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами  .
.
Если  , где a, b – некоторые числа, Pn (x), Qm (x) – многочлены степени n и m соответственно, то
, где a, b – некоторые числа, Pn (x), Qm (x) – многочлены степени n и m соответственно, то 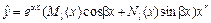 , где
, где 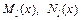 – многочлены степени
– многочлены степени  с неопределенными коэффициентами,
с неопределенными коэффициентами,  ,
,  – число, равное кратности
– число, равное кратности 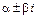 как корня характеристического уравнения
как корня характеристического уравнения  соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами
соответствующего линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами  .
.
20. Система дифференциальных уравнений вида

где  ,
,  ,…,
,…,  – неизвестные функции независимой переменной
– неизвестные функции независимой переменной  , называется нормальной системой.
, называется нормальной системой.
Если правые части нормальной системы дифференциальных уравнений являются линейными функциями относительно  ,
,  ,…,
,…,  , то система дифференциальных уравнений называется линейной.
, то система дифференциальных уравнений называется линейной.
21. а) Если дана система  линейных дифференциальных уравнений с постоянными коэффициентами:
линейных дифференциальных уравнений с постоянными коэффициентами:

то эту систему можно записать в виде одного матричного дифференциального уравнения  , где
, где
 ;
;  ;
;  .
.
Решение системы ищем в виде  ,
,  ,…,
,…,  . Подставив значения
. Подставив значения  ,
,  ,…,
,…,  в систему дифференциальных уравнений, получим систему линейных алгебраических уравнений относительно
в систему дифференциальных уравнений, получим систему линейных алгебраических уравнений относительно  ,
,  ,…,
,…,  :
:

Система должна иметь ненулевое решение, поэтому для определения  получаем уравнение
получаем уравнение  – й степени:
– й степени:

Пусть это характеристическое уравнение имеет  различных корней
различных корней  ,
,  ,…,
,…, 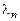 . Тогда система дифференциальных уравнений имеет
. Тогда система дифференциальных уравнений имеет  решений:
решений:
1-е решение, соответствующее корню  :
:
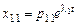 ;
;  ;…;
;…; 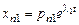
2-е решение, соответствующее корню  :
:
 ;
;  ;…;
;…;  ;
;
…………………………………………………………………….
 – е решение, соответствующее корню
– е решение, соответствующее корню  :
:
 ;
;  ;…;
;…;  .
.
Получена фундаментальная система решений. Общее решение системы имеет вид

Такой способ решения называется решением линейных однородных систем дифференциальных уравнений с постоянными коэффициентами при помощи матриц (видоизмененный метод Эйлера).
б) Иногда нормальную систему дифференциальных уравнений удается свести к одному уравнению  – го порядка, содержащему одну неизвестную функцию. Сведение нормальной системы к одному уравнению может быть достигнуто дифференцированием одного из уравнений системы и исключением всех неизвестных, кроме одного (так называемый метод исключения).
– го порядка, содержащему одну неизвестную функцию. Сведение нормальной системы к одному уравнению может быть достигнуто дифференцированием одного из уравнений системы и исключением всех неизвестных, кроме одного (так называемый метод исключения).
Ряды
1. Пусть дана бесконечная последовательность чисел а 1, а 2, …, аn. Числовым рядом называется сумма вида  .
.
2. Если существует конечный предел 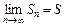 частичной суммы
частичной суммы  , то соответствующий числовой ряд
, то соответствующий числовой ряд 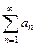 называется сходящимся и его сумма равна S. В противном случае числовой ряд называется расходящимся.
называется сходящимся и его сумма равна S. В противном случае числовой ряд называется расходящимся.
3. Основные свойства сходящихся числовых рядов:
а) Необходимый признак сходимости: если числовой ряд 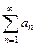 сходится, то
сходится, то  .
.
б) Достаточное условие расходимости: если  , то числовой ряд
, то числовой ряд 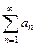 расходится.
расходится.
в) Если все члены сходящегося числового ряда  умножить или разделить на число
умножить или разделить на число  , то получится сходящийся ряд
, то получится сходящийся ряд  .
.
г) Если два сходящихся числовых ряда  и
и  почленно сложить (или вычесть), то получатся сходящиеся ряды
почленно сложить (или вычесть), то получатся сходящиеся ряды  (или
(или 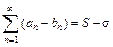 ).
).






