Цели урока: 1) научить учеников пользоваться известным приемом при составлении таблиц деления на 4 и с частным 4;
2) преобразовывать величины и сравнивать их.
3) воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
1. Полоску бумаги длиной 12 см разделили на 3 равные части. Какова длина одной части?
2. В 3 равных пучка связали 15 морковок. Сколько морковок в каждом пучке?
3. Найдите ½ часть числа 18, ⅓ часть числа 18
4. Назовите все числа до 30, которые делятся на 3
5. Найдите ⅓ часть числа 12
6. Найдите ½ часть числа 12
7. Запишите числа до 10, которые делятся на 3
4. Работа по учебнику
(У) Задания 2, 7.
5. Работа в тетрадях
Чтобы ответить на вопрос задачи, надо знать две величины: сколько килограммов вишен сняли и сколько килограммов вишен вмещает одна миска. Вторая величина известна (4 кг), первая — нет.
Чтобы узнать, сколько килограммов вишен сняли, надо знать две величины: сколько килограммов вишен в одном ведре и количество ведер. Эти величины известны — 6 кг и 2 ведра. Зная, сколько килограммов вишен в одном ведре (6 кг) и количество ведер (2), можно найти, сколько всего вишен сняли. Это можно сделать с помощью умножения (надо взять по 6 кг два раза).
Зная общее количество вишен и сколько килограммов вишен вмещает одна миска, можно найти количество мисок с помощью деления (все вишни разложить по 4 кг).
Решение задачи дети оформляют самостоятельно по действиям.
Задание 4. Одно задание выполняется коллективно, остальные — самостоятельно.
3 + 3 + 3 + 15 = 3 • 3 + 15 = 9 + 15 = 24
Физкультминутка
Задание 5*.
 |
Сколько вафель взяла дочь? (4.) Сколько вафель осталось после того, как сын взял половину всех вафель? (8 = 4 • 2.) Сколько вафель взял сын? (8.) Почему? Сколько вафель мама принесла детям? (8 • 2 = 16.)
Задание 6.
Какой из отрезков самый длинный? (Нижний.) Какой из отрезков самый короткий? (Средний.)
 |
Какой может быть длина верхнего отрезка? (Меньше 1 дм, но больше 4 см.)
Построим, например, отрезок, равный 5 см. Тогда второй отрезок — 1 см, третий — 7 см.
6. (Д) Задания 8, 9 (два столбца).
Задание 8. Учитель уточняет, что мастер 42 детали и ученик 38 деталей сделали за 1 день.
(42 - 38) • 7 - 28 (дет.)
Ответ: на 28 деталей больше.
7. Подведение итогов урока
8. Рефлексия
Урок 16
Тема урока. Нахождение ¼ числа.
Цели урока: 1)познакомить учеников с образованием четвертой доли и ее нахождением от числа;
2) преобразовывать величины и выполнять действия над ними.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
За лето школьники собрали 30 кг плодов шиповника, а черники — на 10 кг меньше. Сколько килограммов черники собрали дети?
1. Из полной бочки утром взяли 4 л воды, а вечером — 6 л, в ней осталось еще 20 л воды. Сколько литров воды было в полной бочке?
2. Игровое упражнение "Составьте поезд из примеров" (Учитель раздает детям карточки с записанными математическими выражениями, ученики составляют из них "поезд" так, чтобы ответ примера первого "вагончика" служил началом примера следующего "вагончика")
15 + 10 77 - 47 25 + 25 50 - 43
48 - 33 7 + 70 30 + 18
4. Найдите сумму четырех слагаемых, каждое из которых равно 3 (6, 4, 7, 8, 10)
5. Число 2 умножьте на 4
6. Число 3 умножьте на 5
7. Число 6 умножьте на 4
4. Работа по учебнику
(У) Задание 6*.
Задание 6*. Устанавливаем закономерность, данную в задании.
а) 8 5 8 - 5 = 3 13 7 13 - 7 = 6
3 8 - 3 = 5? 13 - 6 = 7
5 + 3 = 8 6 + 7 = 13
 |
Б)
20:2 = 10
5. Работа в тетрадях
(П) Задания 2, 3, 4, 5, 7, 8.
Задание 2. Вспомнить, какие стороны у квадрата, и дать возможность детям оформить решение задачи самостоятельно.
Задание 3.
3 • 4 + 16 = 28 66 – 32: 4 = 58
48 – 28: 4 = 41 24: 4 + 25 = 31
Задание4.
 |
Способ I.
1) 16-6 = 10 (кг) — стало в первом ящике;
2) 12-5 = 7 (кг) — стало во втором ящике;.
3)10-7 = 3 (кг) — на столько килограммов меньше стало во втором ящике.
Способ II.
1)16-12 = 4 (кг) — на столько больше было в первом ящике;
2) 6-5 = 1 (кг) — на столько больше продали из первого ящика;
3) 10 - 7 = 3 (кг) — на столько килограммов больше стало в первом ящике или меньше во втором.
Ответ: на 3 кг меньше стало во втором ящике.
Физкультминутка
Задание 7. Закономерность: действие выполняем с единицами одного наименования. Для проверки решенных примеров надо использовать линейку с цифрами. 1 дм + 2 см = 10 см + 2 см = 12 см = 1 дм 2 см
1дм
 | |||
 | |||
Задание 8. (10 + 8): 2 = 9 (бидонов)
6. (Д) Задания 9, 10.
Задание 9. Дети составили 4 букета по 3 цветка в
каждом и один букет из 5 цветков. Сколько
цветков они взяли для составления букетов?.
Задание 10. Повторить таблицы деления и умножения на 2, 3 и 4.
7. Подведение итогов урока
8. Рефлексия
Урок 17
Тема урока. Увеличение и уменьшение числа в несколько раз.
Цели урока: 1 ) познакомить учеников с новым видом простых задач на увеличение числа в несколько раз;
2) преобразовывать величины.
3) воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
1. Вычислите, найдите лишнее выражение:
55 - 43 67 – 55 89 - 77
42 - 30 99 - 88 33 - 21
2. Вставьте в окошки нужные числа:
 |
3. Игровое упражнение "Не скажу" (Ученики считают от 1 до 40 по единице. Вместо чисел, которые делятся на 4, говорят: "Не скажу")
4. Работа по учебнику
(У) Задания 1, 5.
Задание 1. Сколько шаров на рисунке у девочки Светы? (3 шара.) Сколько раз по 3 шара у мальчика Вадима? (2 раза.) В таком случае говорят, что у Вадима шаров в 2 раза больше, чем у Светы. Как подсчитать, сколько шаров у Вадима?
3 + 3 = 3-2 = 6 (шаров)
Увеличьте в 2 раза числа 7, 9, 4, 8. Какое арифметическое действие надо выполнить, чтобы число увеличить в 2 раза? (Умножение.)
Задание 5. Какова длина первой полоски? (12 см.) Сколько раз вторая полоска укладывается в первой? (3 раза.) Какая полоска короче? (Вторая.) Во сколько раз? (В 3 раза.) Какое действие надо выполнить, чтобы определить длину второй полоски? (Деление.) Уменьшите в 3 раза числа 15, 21, 30, 6.
5. Работа в тетрадях
(П) Задания 4, 3, 7, 6, 2*.
Задание 2*.
Что дали сыну? (Сыну — две половинки пирожка.)
Что осталось у дочерей? (У дочерей оста лось по
половинке пирожка.) Кто получил больше? (Сын.)
Почему? (Целый пирожок больше половины.) Во сколько раз большее? (В 2 раза.) Во сколько раз меньше получила каждая дочь? (В 2 раза меньше.)
Задание 3. Дети самостоятельно составляют числовые выражения и находят их значения.
16 + 15 16+ (16+ 35) 16:4 (16+ 16): 4
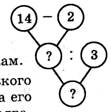Задание 4.
Было — 14 м.
Съела — 2м.
Осталось —?, по? м. трем кроликам.
Задание 6. По периметру маленького квадрата (8 см)
устанавливается длина его стороны.
Во сколько раз периметр квадрата больше длины
его стороны? (В 4 раза). Во сколько раз сторона квадрата меньше его периметра? (В 4 раза.)
8:4 = 2 (см)
Из какого количества сторон маленького квадрата составляется сторона большого квадрата? (Из двух.) Найдите длину большого квадрата.
2 см • 2 = 4 см
Как найти периметр большого квадрата?
4• 4 = 16 (см)
6. (Д) Задания 8, 9.
Задание 9. 13 - 5 = 8 5 + 22 > 25 5 - 2 < 10
16 - 5>10 5 + 5 = 10 5 - 1 = 4
7. Подведение итогов урока
8. Рефлексия
Урок 18 Тема урока. Порядок действий в выражениях без скобок.
Цели урока: 1) познакомить учеников с правилами выполнения действий в выражениях без скобок;
2) повторить названия компонентов действий.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
1. В школьную библиотеку записалось 22 ученика 1 "А" класса и 20 учеников 1 "Б" класса. Сколько всего первоклассников записалось в библиотеку?
2. Для школьной выставки учащиеся 3 "А" класса подготовили 25 рисунков, а учащиеся 3 "Б" класса — на 5 рисунков больше. Сколько рисунков подготовили для
выставки учащиеся 3 "Б" класса? Сколько всего рисунков подготовили для выставки учащиеся двух классов?
3. Найдите ¼от 16, ⅓ от12
4. Какое число больше 7 на 30?
5. Найдите неизвестное слагаемое, если одно слагаемое 20, а сумма 85
6. Чему равно уменьшаемое, если вычитаемое 15, а разность 25?
4. Работа по учебнику
5. Работа в тетрадях
(П) Задания 1,2,4, 3, 7, 5, 6*.
Задание 1. Первый столбец примеров решается коллективно. Сначала ученики читают выражение по последнему действию. Например: «Сумма чисел, где первое слагаемое 29, а второе выражено произведением чисел 7 и 4». Затем проговаривают правила порядка действий и вычисляют. Остальные примеры выполняются самостоятельно.
Задание 2.
1) На каждой из трех веток сидело по 4 птицы. Сколько птиц сидело на трех ветках? 4 • 3 = 12 (пт.)
2) На трех ветках сидело 12 птиц. Сколько птиц сидело на одной ветке, если на каждой ветке сидело птиц поровну?
12:3 = 4(пт.)
3) 12 птиц сели по 4 птицы на ветку. Сколько веток заняли птицы?
12:4 = 3 (ветки)
Задание 4. Закономерности: 1) неизвестное слагаемое находится действием вычитания; 2) неизвестное уменьшаемое — сложением; 3) неизвестное вычитаемое — вычитанием; 4) неизвестный множитель — делением; 6) неизвестный делитель — делением.
Задание 5.
Поиск решения задач можно вести по схемам, построенным на доске. По первой схеме решение задачи в тетради дети выполняют самостоятельно. По второй схеме решение ведется с комментированием.
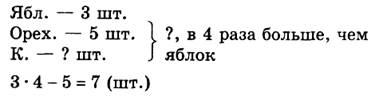Задание 6*.
Задание 7. Что обозначает выражение «сумма длин противоположных сторон»? Какова длина прямоугольника?
12: 2 = 6 (см)
Какова его ширина?
8:2 = 4 (см)
Постройте в тетради такой прямоугольник.
 |
6.
Задание 9. На сколько равных частей разделен прямоугольник? Сколько таких частей закрашено?
а) 3 б) 4
12 9
7. Подведение итогов урока
8. Рефлексия
Урок 19 Тема урока. Уравнение.
Цели урока: 1)ввести понятие «уравнение»;
2) научить решать простейшие уравнения.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
1. Составьте 4 равенства на умножение и деление, используя данные группы чисел:
1) 2,5,10 2) 4,2,8 3) 18,3,6
4) 3,4,12 5)4,20,5 6) 8,4,32
2. Соедините выражения с их значениями:
4 • 9 24 4 • 3 16
4 • 6 36 4 • 4 12
4 • 8 20 4 • 7 40
4 • 5 8 4 •10 4
4 • 2 32 4 • 1 28
3. Определите порядок выполнения действий и вычислите:
36: 4 + 18: 3 49 + 21: 7
39 + 3 • 6 - 18 45 + 32 – 7 • 4
4.В корзине 22 кг яблок, а в ящике 30 кг яблок. На сколько килограммов яблок больше в ящике, чем в корзине? На сколько килограммов яблок меньше в корзине, чем в ящике?
5.Сережа решил 2 столбика примеров, по 6 в каждом. Сколько примеров решил Сережа?
4. Работа по учебнику
(У) Задание 6.
Задание 6. а) Неправильно; б) правильно; в) правильно; г) неправильно;
д) неправильно; е) правильно; ж) правильно.
5. Работа в тетрадях
(П) Задания 1,2,7, 8, 4, 3, 5*.
Знакомство с уравнением можно начать с рассмотрения уже известных равенств с пустым «окошком» + 2 = 5.
Какое число надо подставить в «окошко», чтобы равенство было верным? (3.) Как вы это нашли? (5 — это 2 и 3.) Неизвестное число обозначим цифрой х (икс) и получим запись: х + 2 = 5. Это уравнение. Читается так: икс плюс 2 равно 5. Решить уравнение — это значит найти неизвестное число х. Показывается способ решения уравнения, основанный на связи между компонентами действия сложения. Первое слагаемое — х, второе слагаемое — 2, сумма — 5. Какой компонент неизвестный? Как его найти? (Из суммы надо вычесть известное слагаемое: х=5-2, х=3.) Сделаем проверку: 3 + 2 = 5, 5 = 5.
Учитель знакомит с образцом оформления решения уравнения. Потом ученики под руководством учителя закрепляют способ решения простейших уравнений, выполняя задание 1 из учебника.
Задание 1. Каждое уравнение ученики читают и комментируют решение. Записи решений оформляют по образцу.
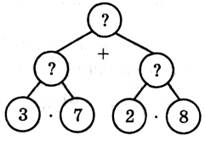Задание 2.
 |
Решение задачи записывается на
доске и в тетради.
Задание 3.
Д. — 12 см
Ш. —?, в 4 раза меньше
Периметр —? см
Как получить отрезок, длина которого в 4 раза меньше длины прямоугольника? (Надо длину прямоугольника разделить на 4.) Чему равна ширина прямоугольника?
12: 4 = 3 (см)
Найдите его периметр разными способами.
Задание 4.
1 + 9 < 20 — правильно; 17 + 9 < 20 — неправильно;
4 + 9 < 20 — правильно; 19 + 9 < 20 — неправильно.
16 + 9 < 20 — неправильно.
Ответ: 1, 4.
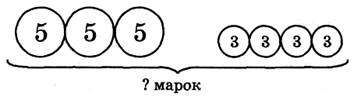
Задание 5*.
Сколько марок у Максима и Глеба вместе? (27 марок.) У кого марок меньше? (У Глеба.) Обозначим марки Глеба отрезком. У кого марок больше? (У Максима.) Во сколько раз? (В 2 раза.) Что это значит? (У него столько же марок, сколько у Глеба, и еще столько же.) Сколько раз надо взять марки Глеба,
чтобы получить такое же количество, как у Максима? (2 раза.) Сколько раз надо взять марки Глеба, чтобы получить 27 марок? (3 раза.) Как узнать, сколько у Глеба марок?
27:3 = 9 (м.)
Сколько марок у Максима?
9 • 2=18 (м.)
Значит, у Глеба 3 набора по 3 марки, остальные марки у Максима. Всего 4 набора, или 18 марок.
5 • 3 + 3 • 1 = 18 (м.)
6. (Д) Задания 9, 10.
Задание 9. По чертежу решается задача.
Сколько раз по 10 страниц
содержат вместе две книги?
(16 + 24): 10 = 4 (раза)
7. Подведение итогов урока
8. Рефлексия
Урок 20
Тема урока. Уравнение.
Цели урока: 1) научить учеников решать простейшие уравнения, у которых неизвестный множитель, делимое, делитель;
2) решать текстовые задачи.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
1. В саду росло 26 яблонь. Осенью посадили еще 20 яблонь.
Сколько яблонь стало в саду? На сколько меньше яблонь было
посажено осенью? На сколько больше яблонь было в саду, чем
посадили осенью?
2.Выразите в сантиметрах: 2 дм 1 см, 1 м, 6 дм 5 см
3.Закончите запись, чтобы она была верной:
7+7+7+7=7•
23 + 23 + 23 = 23 •
4.Найдите ¼ от 24; ⅓ от 18
4. Работа по учебнику
(У) Задания 4, 8.
5. Работа в тетрадях
(П) Задания 1,5,7, 3, 2, 6*.
Задание 3.
 |
Способ I. 20 + 20: 2 = 30 (т.)
Способ II.
 |
20: 2 • 3=30 (т.)
Задание 5. 4 • 9 + 17 = 36 + 17 = 53;
20 + 20:4 = 20 + 5 = 25.
Задание 6*. Запишем начальное положение: 10, 0, 0. В первом ведре — 10 л воды. Во второе ведро можно налить 7 л, поскольку оно пустое; в третье ведро можно налить 3 л. Будем переливать воду из первого ведра в другие и записывать результаты.
Физкультминутка
Задание 7. Выполняется детьми самостоятельно. Во время проверки учитель обращает внимание на 2 способа рассуждений к каждой паре величин. Например:
1 ч < 80 мин 80 мин = (60 + 20)мин
1 ч = 60 мин или 80 мин = 1 ч 20 мин
60 мин < 80 мин 1 ч < 1 ч 20 мин
6. (Д) Задания 9, 10.
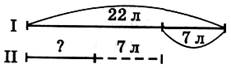Задание 9.
1)22 - 7 = 15 (л) -стало в первом (или втором) бидоне;
2) 15 - 7 = 8 (л) — было во втором бидоне.
7. Подведение итогов урока
8. Рефлексия
Урок 21
Тема урока. Таблица умножения числа 5 и на число 5.
Цели урока: 1)использовать приемы умножения при составлении таблиц;
2) находить доли числа.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
Математический диктант
1.Во сколько раз надо увеличить число 4, чтобы получить 32?
2.Сколько раз по 4 содержит число 16?
3.Если число 6 увеличим в 4 раза, сколько получим?
4.Какое число надо умножить на 3, чтобы получить 27?
5.Первый множитель 8, второй — 4. Найдите произведение
6.Оба множителя 4. Найдите произведение
7.Число 7 умножьте на 4
8.В кружке "Умелые руки" занимается 7 мальчиков, а девочек — в 2 раза больше. Сколько девочек занимается в кружке "Умелые руки"?
9.На школьном участке ученики окопали 20 кустов сирени, а жасмина — в 4 раза меньше. Сколько кустов жасмина окопали ученики?
10.Маме 32 года, а сын в 4 раза младше матери. Сколько лет сыну? На сколько лет мама старше сына?
4. Работа по учебнику
(У) Задание 2.
Задание 2. Закономерность: пользуемся переместительным законом умножения. Рассуждение: 2 • 5 = 5 • 2,
5 • 2 = 10,
значит, 2 • 5 = 10и т. д.
5. Работа в тетрадях
(П) Задания 1,4, 3, 6, 7, 5*.
Задание 4.
 |  | ||
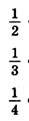от 12 см — это 12: 2 = б см 6 см > 4 см
от 12 см — это 12: 3 = 4 см 6 см > 3 см
от 12 см — это 12: 4 = 3 см 4 см > 3 см
Физкультминутка
Задание 5*. Что значит: у мальчиков конфет стало поровну?
20: 2 = 10 (к }
 |
Когда у Паши стало 10 конфет? (Когда Миша дал ему 5 конфет.) Сколько до этого было конфет у Паши? (5 конфет.) Когда у Миши стало 10 конфет? (Когда он отдал Паше 5 конфет.) Сколько конфет было у Миши? (15 конфет.) Сделайте проверку:
15 + 5 = 20 (к.).
Задание 6. Выполняется коллективно. По схемам ученики составляют следующие уравнения:
х: + 6 = 9; х • 5 = 20; х - 5 = 1.
Задание 7.
30: 5 = 6 (страниц)
6. (Д) Задания 8, 9.
Задание 8. К задаче составляется числовое выражение и находится его значение.
100 - 7 • 3 = 79 (см)
7. Подведение итогов урока
8. Рефлексия
Урок 22
Тема урока. Обратная задача.
Цели урока: 1) научить составлять обратные задачи по рисунку;
2) повторить приемы сравнения числовых выражений.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
Диктант задач
(Учитель читает задачи. Учащиеся записывают в тетради ответ либо решение и ответ. Условия оговариваются до начала диктанта)
1.В баке автомобиля было 40 л бензина. После поездки за город в баке осталось 12 л бензина. Сколько литров бензина было израсходовано на поездку за город?
2.За сентябрь у Оксаны в дневнике появилось 8 десяток, а у Светы — в 2 раза больше. Сколько десяток появилось в дневнике Светы за сентябрь?
3.Школьники убирали яблоки в колхозном саду. Учащиеся 3 "А" класса собрали за день 30 ящиков яблок, а учащиеся 3 "Б" класса — на 5 ящиков меньше. Сколько ящиков яблок собрали учащиеся 3 "Б" класса за день? Сколько всего яблок собрали
третьеклассники за день?
4.Сколько можно сложить квадратов из 16 палочек, если на один квадрат потребуется 4 палочки?
5.Сколько можно сложить треугольников из 15 палочек, если на один треугольник пойдет 3 палочки?
6.У Димы было 9 игрушечных машинок. Ему подарили еще несколько машинок, после этого у Димы стало 12 машинок. Сколько машинок подарили Диме?
4. Работа по учебнику
5. Работа в тетрадях
(П) Задания 1,2,3, 5, 4*.
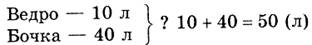Прежде чем приступить к решению задачи, учитель делает объяснения по теме урока. По условию первой задачи делается ее краткая запись и записывается решение.
После этого составляется и решается вторая задача по рисунку а).
 |
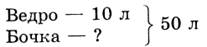50 - 10 = 40 (л)
Что общего в задачах? (Сюжет, числовые данные.)
Чем отличается вторая задача от первой? (В условие второй задачи включили ответ первой задачи — число 50. При этом из условия первой задачи исключили одно из чисел — 40, вместо него поставили вопрос.)
Вторая задача является обратной к первой задаче.
Можно ли к первой задаче составить другую обратную задачу? (Да.)
50 - 40 = 10 (л)
Задание 1. По условию задачи можно оформить таблицу, а затем постепенно ее заполнить, составив две обратные задачи (а, б).
 |
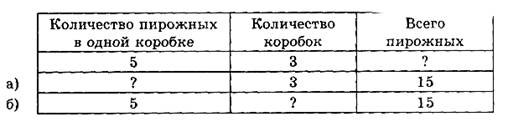Задание 2.
1) 38 + 60 * =56,
38 + 60 = 98,
98 * =56,
98 > 56, значит, из 98 надо вычесть число. Как его найти?
98-56 = 42
Проверка: 38 + 60 - 42 = 56.
Аналогичные рассуждения для равенства 59 + 20 * =34.
2) 34 + 6 = 35 * ,
40 = 35 * ,
40>35, значит, к числу 35 надо прибавить число. Как его найти?
40 - 35 = 5
Проверка: 34 + 6 = 35 + 5.
Аналогичные рассуждения для равенств:
43 + 7 = 48 * и 11-7 = 12 *
3) 13 - 9 > 11 * ,
4>11 * ,
4 < 11, значит, из числа 11 надо вычесть числа, чтобы справа выражение уменьшилось.
4 > 11 - 11 4 >11 - 9
4>11-10 4 > 11 - 8
Задание 3. Можно составить три уравнения.
4 + х = 13 13-х = 4 х + 4 = 13
Физкультминутка
Задание 4*.
 |
Кто купил одинаковое? (Галя и Света купили одно и то же. Света и Лена купили одинаковое.) Сколько девочек купили одно и то же? (3.) Что они купили? (Мороженое.) Кто купил мороженое? (Галя, Света, Лена.) Кто купил разное? (Таня и Света купили разное.) Что купила Света? (Мороженое.) А что — Таня? (Пирожное.) Кто купил еще одно пирожное? (Наташа.)
Задание 5. Чтобы закрасить — прямоугольника, надо разделить его на 2 равные части и закрасить одну из них; чтобы закрасить J-, надо разделить его на 3 равные части и закрасить 2 из них, и т. д.
6. (Д) Задания 6, 7.
Задание 6. По рисунку составляется задача.
 |
Задание 7. Надо выполнить действия и сравнить двузначные числа.
Неверные неравенства:
22 < 53-38 36 + 27 < 29 76 < 92 - 16
98 - 59 > 40 51 - 13 > 60
7. Подведение итогов урока
8. Рефлексия
Урок 23
Тема урока. Составление таблиц деления на 5 и с частным 5.
Цели урока: 1)составить две таблицы деления;
2) повторить единицы времени.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
Математический диктант "Да/нет"
1.Числа при умножении называются множитель, множитель и произведение?
2.От перемены мест множителей произведение изменяется?
3.Чтобы увеличить число в 3 раза, его надо умножить на 3?
4.Чтобы уменьшить число в 4 раза, надо от этого числа отнять 4?
5.Если число 4 умножить на 0, то получится число 4?
6.Если число 1 умножить на 3, то получится число 3?
7.Числа при делении называются делимое, делитель и частное?
8.В выражениях без скобок, содержащих только умножение и деление, действия выполняются в том порядке, как они записаны?
9.В выражениях без скобок первыми выполняются сложение и вычитание, а затем умножение и деление?
10.Чтобы увеличить число на 2, его надо умножить на 2?
4. Работа по учебнику
(У) Задание 6.
Задание 6.
а) 1 ч 40 мин = 60 мин + 40 мин = 100 мин;
б) 70 мин = 60 мин + 10 мин = 1 ч 10 мин.
5. Работа в тетрадях
(П) Задания 1,2,3, 8, 7, 4, 5*.
Задание 1.
2 • 5 = 5 • 2 = 10 10: 5 = 2 10: 2 = 5
3 •5 = 5 • 3 = 15 15: 5 = 3 15: 3 = 5 и т. д.
Задание 2. В тетради можно нарисовать отрезок длиной 10 см (20 клеточек) и разделить его на 5 равных долей.
 |
Задание 3.
Чему равно второе число? (14.) Чему равно третье число? (7.) Как узнать, во сколько раз третье число меньше второго? (14: 7 = 2.)
Физкультминутка
Задание 5*.
 |
Найдите рисунок, на котором показан один предмет. Чем его можно заменить? (Брусок можно заменить кубиком и палочкой.) Заменим
в первом равенстве брусок кубиком и палочкой.
Какой предмет можно забрать из левого и правого рисунков? (Палочку.) Что получим? (Одну палочку можно заменить двумя кубиками.) Обратимся ко второму равенству. Что получим? (Брусок можно заменить тремя кубиками.)
Задание 7.
25 + 19 = 19 + 25 (переместительный закон сложения).
Чтобы сравнить остальные выражения, надо сначала выполнить действия, а потом сравнить полученные числа.
6. (Д) Задания 9, 10.
Задание 9.
М. — 6 шт.
Г. —?, в 3 р. больше, чем мандаринов
Л. —?, в 9 р. меньше, чем груш
1) 6 • 3 = 18 (шт.)
2) 18: 9 = 2 (шт.)
Ответ: 2 лимона.
Ответ на вопрос можно получить при помощи отрезков. Очевидно, что лимонов в 3 раза меньше, чем
мандаринов.
6: 3 = 2 (шт.)
 |
7. Подведение итогов урока
8. Рефлексия
Урок 24
Тема урока. Скорость.
Цели урока: 1)ввести понятие «скорость»; определить связи между понятиями «скорость», «время», «расстояние»;
2) систематизировать знания о единицах времени.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
1.Учитель называет однозначные числа в произвольном порядке. Ученики называют число, которое получится при умножении названного учителем на 3 (4, 5)
2.Учитель называет число, которое является произведением двух других чисел. Учащиеся называют числа, при умножении которых можно получить это число. (Например, 24 — это произведение чисел 4 и 6, 3 и 8)
3.На доске записаны выражения, учащиеся читают их, дополняя недостающую информацию:
1 сут — это... ч
1 ч — это... мин
1 мин — это... с
1 м — это... см
1м — это... дм
4. Найдите 1/5 от 25, 1/4от 12
4. Работа по учебнику
(У) Задания 2, 4, 5*.
Задание 2.
1-й циферблат: 4 ч (утра) или 16 ч.
Через 5 часов: 9 ч или 21 ч.
Задание 5*. Позавчера, вчера, сегодня, завтра, послезавтра.
5. Работа в тетрадях
(П) Задания 1,6, 3, 7.
Задание 1. С помощью чертежа решается задача:
20: 2 = 10 (м).
Как нашли скорость? (Расстояние разделили на время.) Находим запись этой задачи в таблице (первая строка).
Формулируется вывод: чтобы найти скорость, надо расстояние разделить на время.
Затем ученики по таблице составляют и решают две обратные задачи.
Формулируются выводы:
чтобы найти расстояние, надо скорость умножить на время;
чтобы найти время, надо расстояние разделить на скорость.
Физкультминутка
Задание 3.
а: 1. Надо найти такое число, которое при умножении на 1 дает а. Это число а. Значит, a: 1 = a.
(7: 1 = 7; 21:1 = 21.)
а: а. Надо найти такое число, которое при умножении на а дает а. Это число 1. Значит, а: а = 1. (5: 5 = 1; 12: 12 = 1; 28: 28 = 1 и т. д.)
0: а. Надо подобрать такое число, которое при умножении на а дает 0. Это число 0. Значит, 0: а = 0. (0:3 = 0.)
Задание 6.
х + 17 = 40
х = 40 - 17
x = 23
23 + 17 = 40
40 = 40
Задание 7. Самостоятельная работа по вариантам.
6. (Д) Задания 8, 9.
Задание 8.
 |
7. Подведение итогов урока
8. Рефлексия
Урок 25
Тема урока. Классификация треугольников по длине сторон.
Цели урока: 1)дать понятие равностороннего, равнобедренного и разностороннего треугольников;
2) закрепить таблицы умножения и деления.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
1.За 2 ч пешеход прошел 10 км. Найдите его скорость
2.Скорость пешехода 5 км/ч. Какое расстояние он пройдет за 3 часа?
3.Увеличьте 4 в 6 раз; 3 в 4 раза
4.Уменьшите 24 в 3 раза; 27 в 9 раз
5.Сравните:
50 см и 5 дм
60 с и 1 ч
60 мин и 1 ч
4. Работа по учебнику
5. Работа в тетрадях
(П) Задания 1, 2, 3, 4, 7, 6, 5*.
Задание 1. ВАК, KCD — разносторонние треугольники, ВКС — равнобедренный треугольник.
Задание 2.
 |
При решении задачи надо задать такие вопросы:
«Что обозначает число 35?» (Количество грибов
в первой корзине.) «Что обозначает число 5?» (Во сколько раз меньше количество грибов во второй корзине.) «Как по числам 35 и 5 установить, сколько грибов во второй корзине?» (35: 5.)
Задание 3. Дети комментируют решения уравнений, проговаривая правила нахождения неизвестных компонентов действий.
Физкультминутка
Задание 5*.
 |
Способ I.
Дочь получила: 3 + 3 + 3 =9 (абрикосов).
Сын получил: 2 + 2 + 2 = 6 (абрикосов).
 |
Способ II.
Дочь получила: 3 • 3 = 9 (абрикосов).
Сын получил: 2 •3 = 6 (абрикосов).
Способ III. Сколько абрикосов получили дочь и сын за один раз? (5 = 3 + 2.) Сколько раз они получали по 5 абрикосов? (3 раза, 15: 5.) Сколько абрикосов получила дочь? (9 = 3 • 3.) Сколько абрикосов получил сын? (6 = 2 • 3.)
Задание 7. По краткой записи условия задачи дети составляют задачу: «В хозяйстве было несколько цыплят. Вырастили еще 70, и стало 97 цыплят. Сколько цыплят было в хозяйстве?»
Было больше или меньше, чем 97 цыплят? (Меньше.) Как узнать, сколько цыплят было в хозяйстве? (97-70 = 27.)
К этой задаче можно составить две обратные.
1) В хозяйстве было 27 цыплят. После того как вырастили несколько цыплят, в хозяйстве стало 97 цыплят. Сколько цыплят вырастили?
Цыплят вырастили больше, чем 97, или меньше? (Меньше.) Как узнать, сколько цыплят вырастили?
(97-27 = 70.)
2) В хозяйстве было 27 цыплят. Вырастили еще 70. Сколько цыплят стало в хозяйстве? Эту задачу дети решают самостоятельно.
6. (Д) Задание 8.
Задание 8. По краткой записи решения задачи можно составить числовое выражение:
7. Подведение итогов урока
8. Рефлексия
У рок 26
Тема урока. Умножение числа 6 и на число 6.
Цели урока: 1) составить две таблицы умножения;
2) вести работу с числовыми и буквенными выражениями.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
Математический диктант
1.Чему равно произведение чисел 4 и 4?
2.Число 5 увеличьте в 4 раза
3.Делимое 28, делитель 4. Чему равно частное?
4.Первый множитель 8, второй — 5. Чему равно произведение?
5.Число 24 уменьшите в 3 раза
6.Неизвестное число увеличили на 5 и получили 15. Чему равно неизвестное число?
7.Сколько секунд в одной минуте?
8.15 роз надо поставить в 3 вазочки. Сколько роз будет в каждой вазочке?
9.В телевизионной игре "Спортландия" участвовало 3 команды, по 8 человек в каждой. Сколько всего человек принимало участие в "Спортландии"?
10.Из 28 кубиков Света построила 4 одинаковые башни. Сколько кубиков в каждой башне?
11.За столом сидела вся семья: мама, папа, дочка, сын и бабушка. Каждый съел по 2 пирожка. Сколько пирожков съели все члены семьи?
4. Работа по учебнику
(У) Задания 8, 2.
Задание 2.
Используем переместительный закон умножения: 7 • 6 = 6 • 7, 6 • 7 = 42, значит, 7 • 6 = 42 и т. д.
Задание 8. На сколько равных частей разделена каждая фигура? Сколько таких частей закрашено?
 |
5. Работа в тетрадях
(П) Задания 1,4, 3, 5*. 6, 7.
Задание 3.
Задание 4. Задание выполняется на доске и в тетрадях.
Задание 5*.
На вторых весах: 3 арбуза весят 12 кг. Значит, сколько весит один арбуз? (4 кг.) На первых весах:
 |
Ответ: тыква весит 7 кг.
Физкультминутка
Задание 6. Уравнение х • 5 = 50 дети решают способом подбора.
Задание 7.
6. (Д) Задания 9, 10.
Задание 9.
I — 12 р.
II —? р., на 4 р. меньше
III —? р., на 6 р. больше, чем на I и II
12 + (12 - 4) + 6 — растений на третьем участке.
7. Подведение итогов урока
8. Рефлексия
Урок 27
Тема урока. Таблицы деления на 6 и с частным 6.
Цели урока: 1)составить две таблицы на деление;
2) работать с отношениями «больше на», «больше в».
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
1.Составьте 2 примера на сложение с ответом 15
2.Составьте 2 примера на умножение с ответом 24
3.В классе 8 мальчиков и 15 девочек. 3 девочки отсутствуют по болезни. Сколько девочек присутствует в классе? Сколько всего детей присутствует в классе?
4.Пешеход шел со скоростью 5 км/ч и прошел 10 км. Сколько времени шел пешеход?
4. Работа по учебнику
5. Работа в тетрадях
(П) Задания 1, 2, 4, 7 (один столбец), 5, 3, 6*.
Задание 3. Сначала надо найти ½ — от 8 см (4 см), потом увеличить 4 см в 3 раза (12 см) и построить отрезок длиной 12 см.
Можно отрезок 4 см последовательно отложить 3 раза.
Задание 4. (Прием проб и ошибок.)
6-(4-2) = 12 31-(10-3)-24 (12:2): 2 = 3
(6-2)-3-12 (40-15): 5-5 (16: 4)-2 = 8
Физкультминутка
Задание 5.
IIIкл. — 15 уч.
IIкл. —?, на 3 уч. больше
I кл. —?, в 2 раза меньше, чем II кл.
При ответе на вопрос, что обозначают выражения, дети пишут в тетради краткие объяснения.
15 + 3 = 18 (уч. второго класса).
(15 + 3): 2 = 9 (уч. первого класса).
15 + (15 + 3) + (15+ 3): 2 = 42 (уч. третьего, второго и первого классов).
Сколько учеников второго класса пошло в поход? (18 учеников.) Сколько учеников первого класса пошло в поход? (9 учеников.)
Как узнать, во сколько раз меньше пошло в поход учеников первого класса, чем второго?
18: 9 = 2 (раза)
Задание 6*.
Н. — 4 шт.
Т. — 5 шт.
Г. —?
Т. и Г. —?, в 3 раза больше, чем Н.
4 • 3 = 12 (шт.) — тюльпанов и гвоздик;
12 - 5 = 7 (шт.) — гвоздик.
6. (Д) Задания 7 (два столбца), 8.
Задание 8.
Л. — 18 д.
Д. —?, в 2 р. меньше, чем у Л.
Р. —?, на 15 д. больше, чем у Д.
7. Подведение итогов урока
8. Рефлексия
Урок 28
Тема урока. Классификация треугольников по углам.
Цели урока: 1 ) познакомить учеников с остроугольным, прямоугольным и тупоугольным треугольниками;
2) решать уравнения нового вида.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
1.Представьте числа суммой одинаковых слагаемых:
18= □+ □
18= □+ □+ □
18= +++++
24 = □ + □
24 = □ + □ + □
24 =□+□+□+□+□+□
2.К пиджаку пришили пуговицы двумя одинаковыми рядами, по 6 пуговиц в каждом ряду. Сколько всего пуговиц пришили к пиджаку?
3.Длина одного отрезка 12 см, а другого — в 2 раза меньше.
Вычислите длину второго отрезка
4. Работа по учебнику
(У) Задания 1, 4.
Задание l. ABK, BKD, BDC — прямоугольные треугольники.
ABD — остроугольный треугольник.
Задание 4. Прочитайте левую часть первого уравнения: 7 + 3 + х. Какое действие легко выполнить в этом выражении? (7 + 3.) Выполним его. Что получится в левой части уравнения? (10 + х.) Соединим левую и правую части уравнения. Что получим? (10 + х = 14.) Как найти неизвестное слагаемое?
Аналогично проводится работа со вторым уравнением.
5. Работа в тетрадях
(П) Задания 3, 2, 5, 6*.
Задание 2.
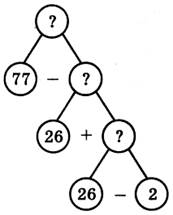
В трех коробках лежало 77 пачек чая.
В первой было 26 пачек, во второй коробке на 2 пачки
меньше. Сколько пачек было в третьей коробке?
Задание 3.
I — 50
II — 26
III —?, в 6 раз меньше, чем (50 - 26)
Физкультминутка
Задание 6*.
45 - 6 = 39— Б
6 • 5 - 5 = 25—е
21:3 + 7 = 14—л
24 - 14 = 10—а
90 - 30: 6 = 85—р
42 - (21 - 5) = 26—у
3 • 6 + 18: 3 = 24 —с
30 – 8: 4 = 28— ь
6. (Д) Задания 7, 8.
Задание 7. Что значит: второй отрезок в 4 раза короче первого? (Он равен ¼ от первого отрезка.) Как определить длину второго отрезка? (1 дм 6 см: 4.) Дети самостоятельно рисуют два отрезка: 16 см и 4 см.
Как определить, во сколько раз первый отрезок длиннее второго?
16: 4 = 4 (раза)
Задание 8.
Ошибки:
50 - 27 = 37 64 + 28 = 82 57 + 23 = 70
81 - 26 = 65 78 + 19 = 76
7. Подведение итогов урока
8. Рефлексия
Урок 29
Тема урока. Сравнение долей.
Цели урока: 1) научить сравнивать доли с помощью наглядности;
2) сравнивать числовые выражения и величины.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
Решите, запишите только ответы:
Вариант 1 Вариант 2
5 • 6 36:6 4 • 5 30:6
4 • 8 48:6 9 • 4 42:6
3 • 9 24:3 3 • 8 24:4
7 • 2 27:9 7 • 3 36:9
6 • 3 45:5 6 • 4 54:6
(У) Задания 1,2, 8.
Задание 1. После работы с рисунком можно ответить на дополнительные вопросы: «Какая доля самая маленькая?», «Какая доля самая большая?», «Назови доли по убыванию», «Назови доли по возрастанию».
Можно сформулировать закономерность: чем на большее число делим целое, тем меньшую долю получаем.
5. Работа в тетрадях
(П) Задания 7, 3, 4, 6, 5*.
Задание 3.
 |
План решения задачи:
1)Сколько ящиков с помидорами продали за день?
5 + 4 = 9 (ящ.)
2)Сколько килограммов помидоров продали за весь день?
6 • 9 = 54 (кг)
Для проверки решения задачи можно использовать
второй способ ее решения.
1) 6 • 5 = 30 (кг)
2) 6 • 4 = 24 (кг)
3) 30 + 24 = 54 (кг)
Вывод: 6 • (5 + 4) = 6 • 5 + 6 • 4 — число 6 умножили на каждое слагаемое, а результаты сложили.
Физкультминутка
Задание 4. Самостоятельное решение уравнений по вариантам (I вариант — 1-й ряд; II вариант — 2-й ряд).
Задание 5*. Что обозначает число 22 кг? (22 кг весит канистра, наполненная бензином.) Что обозначает число 12 кг? (12 кг весит канистра и половина того бензина, что был сначала.) Почему канистра с бензином стала весить меньше? (Отлили половину бензина.) Можно ли определить, сколько бензина отлили из канистры? (Можно.) Как?
22 – 12 = 10 (кг)
Что обозначает число 10 кг? (10 кг бензина осталось, и 10 кг бензина отлили.) Можно ли ответить на вопрос задачи? (Можно.) Как?
12 - 10 = 2 (кг) или 22 - (10 + 10) = 2 (кг)
Задание 6. Прием проб во время коллективной работы приводит к такой расстановке скобок.
(5 • 2) + (2: 2) = 11 (можно скобки и не ставить)
5 • (2 + 2: 2) = 15
(2 • 5 + 4): 2 = 7
(2 • 5) + (4: 2) = 12 (можно скобки и не ставить)
6. (Д) Задания 9, 10.
Задание 9.
 |
 |
? 6 + 6 • 4 = 30 (аист.)
Запись условия задачи при помощи отрезков подсказывает другой способ решения задачи:
6 • (1 + 4) = 30 (аистят).
7. Подведение итогов урока
8. Рефлексия
Урок 30
Тема урока. Решение задач на кратное сравнение.
Цели урока: 1) показать решение простых задач нового вида — на кратное сравнение;
2) закрепить выученные таблицы умножения и деления.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
Запишите выражения и вычислите их значения
1.На одной полке 25 книг, а на второй — 17. На сколько меньше книг на второй полке?
2.Разность чисел 13 и 6 увеличьте на 8
3.Сумму чисел 4 и 7 уменьшите на 9
4.Сумму чисел 27 и 3 увеличьте на 30
5.Разность чисел 65 и 5 увеличьте на 8
6.Разность чисел 90 и 60 уменьшите на 30
4. Работа в тетрадях
(П) Задания 1,3,4, 2, 6, 5*, 7.
Задание 1.
 |
Сравниваются краткие записи условий задач и их решения.
Задание 2. Задание выполняется на доске и в тетради.
Физкультминутка
Задание 3.
1) 30: 5 = 6 (чел.) — составляет одна часть (столько девочек);
2) 30 + 6 =36 (чел.) или 6 • 6 = 36 (чел.) — всего детей.
Задание 4. АО = ОМ = МК = КТ = ТЕ = 7 см.
Ученики самостоятельно находят длину ломаной линии: 35 см = 3 дм и 5 см. Задание 5*.
 |
Ответ: 4 способа.
Задание 7. По краткой записи можно составить, например, такую задачу: «В одном ящике было 28 кг яблок, а во втором — 26 кг. Детям раздали 37 кг яблок. Сколько яблок осталось?».
5. (Д) Задания 8, 9.
6. Подведение итогов урока
7. Рефлексия
Урок 31
Тема урока. Задачи на нахождение четвертого пропорционального. Способ приведения к единице.
Цели урока: 1)ввести новый вид составных задач на нахождение четвертого пропорционального;
2) закрепить таблицы умножения и деления.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
Диктант задач
1.Олег решил 18 примеров и записал их в 3 равных столбика. Сколько примеров записал Олег в каждый столбик?
2.На решение примеров Ксюша потратила 8 мин, а на выполнение задания по русскому языку — в 2 раза больше времени. Сколько времени понадобилось Ксюше для выполнения задания по русскому языку?
3.На дачном участке растет 8 сливовых деревьев, а яблонь —на 2 меньше. Сколько яблонь растет на дачном участке? Объясните решение
4.18 карандашей разложили в коробки, по 6 штук в каждой. Сколько понадобилось коробок?
5.За прошедшую неделю Егор получил четыре десятки, а за эту — в 2 раза больше. Сколько десяток появилось в дневнике у Егора за эту неделю? За две последние недели?
6.Костя решил 18 примеров, Витя — 9 примеров. На сколько примеров меньше решил Витя? Во сколько раз больше решил примеров Костя?
7.Артуру 15 лет. Его сестре Оле — 5. На сколько лет Артур старше Оли? Во сколько раз Оля младше Артура?
4. Работа в тетрадях
(П) Задания 1, 2, 6, 3, 5, 4*, 7.
Задание 1.
54: 6 42: 6 36: 4 27 - 9
9 • 3 18 + 26 8 • 6 28 + 6
Обобщение, формулировка закономерностей: уменьшить в несколько раз — разделить; увеличить в несколько раз — умножить; уменьшить на несколько единиц — вычесть; увеличить на несколько единиц — сложить.
Задание 2.
 |
1) 10: 5 = 2 (кг)
2) 2 • 2 = 4 (кг)
3) 10 - 4 = 6(кг) — останется
На второй вопрос можно ответить по-другому.
2 • (5 - 2) = 6 (кг)
Задание 3. АВ = 5 см; МК = 10 см.
1) 10: 5 = 2 (раза)
2) 10 - 5 = 5 (см)
Физкультминутка
Задание 4*. Разбиваем составную задачу на две простые.
1) Дядя Артем за 2 ч проехал на лошади 18 км. Какой вопрос можно поставить к этой задаче? (Сколько километров дядя Артем проехал за 1 ч?) Как узнать?
18: 2 = 9 (км/ч)
Как называют величину 9 км/ч?
(Скорость.)
2) Дядя Артем едет на лошади со скоростью 9 км/ч.
Какое расстояние он проедет за 5 ч?
9 • 5 = 45 (км)
 |
Задание 5. Треугольник
можно построить коллектив-
но. Нарисовать отрезок дли-
ной 4 см иразделить его по-
полам. От середины отрезка
отсчитать вниз 9 клеточек и
отметить точку С. Эту точ-
ку соединить с концами от-
резка.
АВ = 4см,
АС = СВ = 5 см
5 • 2 + 4 = 14 (см)
Задание 6. Задание выполняется детьми самостоятельно.
5. (Д) Задание 8, 9.
Задание 8.
 |
6. Подведение итогов урока
7. Рефлексия
Урок 32
Тема урока. Таблица умножения числа 7 и на число 7.
Цели урока: 1)составить две таблицы на умножение;
2) решать задачи на нахождение четвертого пропорционального.
3)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего
