Проекции прямых
Классификация прямых по расположению в пространстве.
Прямые общего положения – не перпендикулярные и не параллельные ни к одной из плоскостей проекций: П1, П2, П3
Прямые частного положения – параллельные или перпендикулярные к одной из плоскостей проекций.
Прямые уровня – параллельные одной из плоскостей проекций.
Горизонтальная прямая (горизонталь) – прямая, параллельная горизонтальной плоскости проекций П1.
Фронтальная прямая (фронталь) – прямая, параллельная фронтальной плоскости проекций П2.
Профильная прямая – прямая, параллельная фронтальной плоскости проекций П3.
Проецирующие прямые – перпендикулярные одной из плоскостей проекций.
Горизонтально проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций П1.
Фронтально проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций П2.
Профильно проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций П3.
|
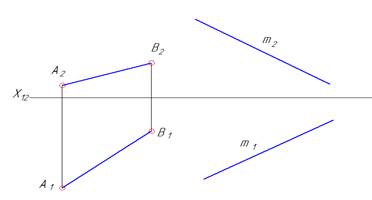
| Пример прямых общего положения на двухкартинном комплексном чертеже. Прямая АВ: при движении произвольной точки по прямой в сторону уменьшения абсциссы (X) - высота точки (Z) на прямой увеличивается; - глубина (Y)- уменьшается; - расстояние до плоскости П2 уменьшается; - расстояние до плоскости П3 уменьшается. Прямая m: при движении произвольной точки по прямой в сторону приближения к плоскости П3 - высота точки уменьшается; - глубина уменьшается. |
|
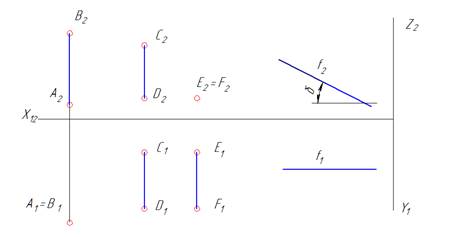
| Пример некоторых прямых частного положения. АВ – горизонтально проецирующая прямая. А и В – горизонтально конкурирующие точки. Фронтальная проекция показывает, что точка В расположена выше точки А. CD – профильная прямая. Точка С расположена выше точки D (это показывает фронтальная проекция); точка D расположена ближе к наблюдателю по сравнению с точкой С (показывает горизонтальная проекция). EF – фронтально проецирующая прямая. E и F - фронтально конкурирующие точки. Горизонтальная проекция показывает, что точка F расположена ближе к наблюдателю по сравнению с точкой E. Прямая f – фронталь, расположена параллельно плоскости проекций П2. Натуральная величина угла наклона f к плоскости проекций П1 видна на фронтальной проекции. |
Следы прямой
| Следом прямой называется точка пересечения прямой с плоскостью проекций. Горизонтальным следом прямой называется точка пересечения прямой с горизонтальной плоскостью проекций. Фронтальным следом прямой называется точка пересечения прямой с фронтальной плоскостью проекций. Профильным следом прямой называется точка пересечения прямой с профильной плоскостью проекций. |
|
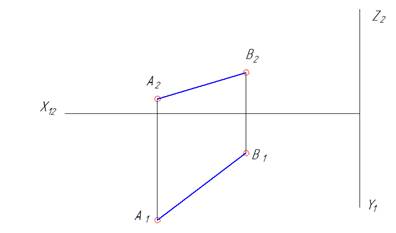
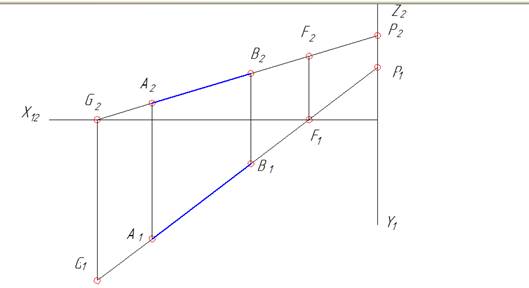
| Дана прямая АВ. Требуется построить горизонтальный, фронтальный и профильный следы прямой АВ. Обоснование алгоритма: Для поиска горизонтального следа нужно на прямой АВ найти точку, которая имеет высоту Z=0. Точка пересечения прямой АВ с плоскостью проекций удовлетворяет двум условиям: 1)принадлежит прямой АВ; 2)имеет высоту Z=0. Следует перемещаться по прямой АВ в сторону уменьшения координаты Z до достижения Z=0. Такой точкой будет точка G. Для определения фронтального следа на прямой АВ нужно выбрать точку с глубиной Y=0. Такой точкой является точка F. Для определения профильного следа на прямой АВ нужно найти точку с широтой Х=0. Такой точкой в данном случае является точка Р, расположенная во второй четверти (квадранте). |
|
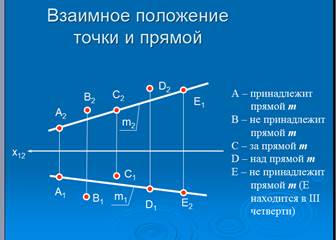
Взаимное положение точки и прямой
| При изучении центральной проекции в лекции №1 одно из свойств состояло в следующем: точка на прямой проецируется в точку на проекции этой прямой. Поэтому при определении принадлежности точки к прямой по комплексному чертежу следует сопоставить взаимное расположение одноименных проекций точки и прямой: если проекции точки принадлежат одноименным проекциям прямой, то точка принадлежит данной прямой. Примеры взаимного положения точек и прямой m: |
|
| В данном примере следует обратить внимание на точку Е, которая не принадлежит прямой m, потому что проекция Е1 не принадлежит m1, и Е2 не принадлежит m2. |
Взаимное положение прямых
Из школьного курса геометрии известны возможные взаимные положения прямых:
| ||

| 
| 
|




