Оборудование: магазин емкостей, исследуемые конденсаторы, источник переменного тока, телефон, реостат со шкалой.
1.Теоретическое введение. Описание лабораторной установки и метода измерения
Электроемкостью или просто емкостью уединенного проводника называется физическая величина, численно равная количеству электричества, которое нужно сообщить проводнику, чтобы его потенциал изменился на единицу:
(1)
где С - емкость проводника,
j - потенциал,
q - количество электричества.
Электроемкость зависит от формы проводника, его линейных размеров, от расстояния этого проводника относительно других и диэлектрической проницаемости среды, в которой находится проводник.
Если около проводника имеются другие проводники, то его емкость больше, чем у такого же уединенного проводника. Система проводников, предназначенных для образования значительной емкости, называется конденсатором.
Емкость конденсатора равна:
, (2)
где q- заряд одного из электродов конденсатора,
U =j1-j2 - разность потенциалов проводников, составляющих конденсатор.
Плоский конденсатор состоит из двух параллельных металлических пластин, площадью S каждая, расположенных на расстоянии d друг от друга. Его электроемкость равна:
, (3)
где e - диэлектрическая проницаемость среды, заполняющей пространство между пластинами,
e0 - электрическая постоянная.
Общая емкость конденсаторов при последовательном и параллельном соединении рассчитывается по следующим формулам:
(2)
(3)
где Сi - емкость конденсатора,
n - число конденсаторов.
Для постоянного тока конденсатор представляет бесконечно большое сопротивление. В цепи переменного тока конденсатор представляет собой емкостное сопротивление:
, (4)
зависящее от круговой частоты переменного тока (w=2 pn; n = 50 Гц).
Поэтому измерить емкость конденсатора можно при помощи мостовой схемы, в которой источник постоянного тока заменяется источником переменного тока.
Рассмотрим схему на рис. 1. Здесь источник переменного тока (~) выпрямитель ВС-24 (рис.2а). СХ – неизвестный конденсатор (рис.2б), С – магазин конденсаторов с известным набором емкостей (рис.2в), Точки М и К – нижние клеммы реостата, точка В – верхняя подвижная часть реостата (рис.2г). Т – телефон (рис.2д).
Если к точкам А и В подведен переменный ток, то измерительный прибор, включенный в мост между точками М и К покажет некоторый ток, т.к. потенциалы точек М и К различны. Подобрав надлежащим образом сопротивления R1 и R2 можно добиться, чтобы ток в измерительном приборе отсутствовал.
В нашем случае в качестве измерительного прибора включен телефон. Звук в телефоне исчезает, когда ток Iт = 0. При этом потенциалы точек М и К будут равны jМ = jК значит разности потенциалов на сопротивлениях R1 и R2 будут равны. Обозначим силы токов на сопротивлениях R1 и R2 буквами I1 и I2. На основании закона Ома можно записать:
I1 R1 = I2 R2 (5)
Точно также, будут равны разности потенциалов на конденсаторах Сх и С. Учитывая зависимость сопротивления конденсаторов от емкости и частоты тока, можно записать:
(6)
Разделив почленно (5) на (6), получим: R1 Сх = R2 С или 
- условие равновесия моста, т.е. отсутствия тока в телефоне.
Т.к. сопротивление проводника пропорционально его длине (
), то отношение сопротивлений можно заменить отношением длин 
. Тогда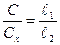 
,
откуда: 
(7)
Если емкость конденсатора С известна, то емкость Сх можно определить по формуле (7), добившись путем изменения сопротивлений R1 и R2 отсутствия тока в телефоне.
2.Порядок выполнения работы
1. Соберите схему по рис. 1. В качестве известного конденсатора используется магазин емкостей, вместо сопротивлений R1 и R2 включают реостат на три точки. Точка В - движок реостата, соответствует верхней клемме реостата (рис. 2г).
2. Установите напряжение 8-10В. Установив на магазине емкостей 2 мкФ, подберите на реостате такое положение ползунка, при котором ток по телефону не потечет (звук отсутствует).
3. Повторите измерения, установив на магазине емкостей значения 1мкФ и 0,5мкФ.
4. Повторите измерения для второго конденсатора.
3. Обработка результатов измерения
1. По формуле (7) подсчитайте Сх. Результаты занести в таблицу.
2. Подсчитайте среднее значение Схср по формуле: 
3. Подсчитайте среднюю ошибку DСхср: 
4. Подсчитайте абсолютную ошибку e по формуле: 
5. Результат запишите в виде: С = Схср ±ΔСхср.
6. Повторите пункты 1-5 для второго конденсатора.
7. Сделайте вывод по работе.
Таблица
| № | С, мкФ | ℓ1, см | ℓ2, см | Сх, мкФ | Схср, мкФ | DСхср, мкФ | e, % |
| 0,5 | |||||||
| С = Схср ±ΔСхср С= | |||||||
| 0,5 | |||||||
| С = Схср ±ΔСхср С= |
ВОПРОСЫ:
1. Что называется электроемкостью проводника? От чего она зависит? Единицы измерения.
2. Что такое конденсатор? Виды конденсаторов. Электроемкость конденсаторов.
3. Соединения конденсаторов.
4. Законы Кирхгофа.
5. Применение законов Кирхгофа к объяснению схемы моста.
6. Емкостное сопротивление.
7. Чем отличается схема моста Уинстона от схемы, используемой в данной работе? Почему?
8. Что такое магазин емкостей?
9. Методы определения электроемкости конденсатора.
ЛАБОРАТОРНАЯ РАБОТА № 3
